
- •Мфюа. Маси. Кафедра оменд 2015
- •Математика часть 1. Линейная алгебра. Лекция 1.
- •Тема 1. Векторная алгебра.
- •П.1. Системы координат на плоскости и в пространстве.
- •П.2. Векторы.
- •П.2.2. Координаты вектора. Координатная запись вектора. П.3. Скалярное произведение векторов и его свойства.
- •Вычисление угла между векторами Из определения скалярного произведения и формул (2.5), (2.9) следует, что
- •Условие перпендикулярности векторов
- •П.4. Векторное произведение векторов и его свойства.
- •Свойства векторного произведения векторов
- •П.5. Смешанное произведение векторов и его свойства.
- •Вычисление объема тетраэдра и параллелепипеда, построенного на векторах (рис. 2.10).
- •Вычисление высоты тетраэдра (параллелепипеда).
- •Условие компланарности векторов (теорема 2.1):
- •Задание на Дом:
- •Тема 1. Векторная алгебра.
- •Тема 2. Матрицы и определители. П.2.1. Понятие матрицы
- •1.5. Действия над матрицами
- •П.2.2. Определители.
- •Разложение определителя по строке или столбцу
- •Тема 6. Аналитическая геометрия.
- •1.Уравнение прямой по угловому коэффициенту и точке:
- •3.Уравнение прямой по точке и направляющему вектору:
- •4.Уравнение прямой по двум точкам.
- •Уравнение прямой в отрезках имеет вид , где – ненулевые константы.
- •И, наконец, последний нами рассматриваемый тип уравнения прямой:
- •7.Уравнение прямой в параметрической форме:
- •П.6.2. Взаимное расположение двух прямых
- •6.6. Кривые второго порядка. Окружность
- •2. Эллипс.
- •4. Гипербола
- •4. Парабола
- •П.6.7. Поверхности второго порядка.
- •2. Эллипсоиды.
- •3.Цилиндрические поверхности.
- •4. Конические поверхности.
- •5. Гиперболоиды.
- •6.Параболоиды.
- •Литература.
- •Данко п.Е. И др. Высшая математика в упражнениях и задачах: в 2-х томах. – м.: Высшая школа, 2010.
- •Письменный д.Т. Конспект лекций по высшей математике: – м.: Айрис-пресс, 2007. -608 с.: ил. –(Высшее образование), isbn 5-8112-2893-7, 978-5-8112-2893-5.
- •Математика для заочников http://www.Mathprofi.Ru
Мфюа. Маси. Кафедра оменд 2015
Соболева В.В.
Математика часть 1. Линейная алгебра. Лекция 1.
Тема 1. Векторная алгебра.
План лекции:
Системы координат на плоскости и в пространстве.
Векторы и их свойства.
Скалярное произведение векторов, его свойства, физический и геометрический смысл.
Векторное произведение векторов, его свойства, физический и геометрический смысл.
Смешанное произведение трех векторов, его свойства и геометрический смысл.
П.1. Системы координат на плоскости и в пространстве.
П.1.1. Системы
координат на плоскости
Декартовы
прямоугольные координаты (рис.
4.1)
О -
начало координат, Ох -
ось абсцисс, Оy -
ось ординат, ![]() -
базисные векторы,
-
базисные векторы, ![]() -
абсцисса точки M (
-
абсцисса точки M (![]() -
проекция точки M на
ось Ох параллельно
оси Оy),
-
проекция точки M на
ось Ох параллельно
оси Оy), ![]() -
ордината точки M (
-
ордината точки M (![]() -
проекция точки M на
ось Oyпараллельно
оси Ox).
-
проекция точки M на
ось Oyпараллельно
оси Ox).



Декартовы косоугольные (афинные) координаты (рис. 4.2)
О -
начало координат, ![]() -
оси координат,
-
оси координат, ![]() ,
, ![]() -
координаты точки M (
-
координаты точки M (![]() -
проекция точки M на ось
-
проекция точки M на ось ![]() параллельно
оси
параллельно
оси ![]() ,
аналогично
,
аналогично ![]() ),
), ![]() -
базисные векторы.
-
базисные векторы.
П.1.2.Системы
координат в пространстве
Декартовы
прямоугольные координаты (рис.
4.4)
О -
начало координат, Ох -
ось абсцисс, Оy -
ось ординат, Оz -
ось аппликат,![]() -
базисные векторы. Oxy, Oxz, Oyz -
координатные плоскости,
-
абсцисса точки M (
-
проекция точки M на
ось Охпараллельно
плоскости Оyz),
-
ордината точки M (
-
проекция точки M на
ось Oy параллельно
плоскости Oxz),
-
базисные векторы. Oxy, Oxz, Oyz -
координатные плоскости,
-
абсцисса точки M (
-
проекция точки M на
ось Охпараллельно
плоскости Оyz),
-
ордината точки M (
-
проекция точки M на
ось Oy параллельно
плоскости Oxz),![]() -
ордината точки M (
-
ордината точки M (![]() -
проекция точки M на
ось Oz параллельно
плоскости Oxy).
-
проекция точки M на
ось Oz параллельно
плоскости Oxy).

П.2. Векторы.
Направленный
отрезок
с началом в точке А
и концом в точке В
называется геометрическим вектором
или просто вектором. Обозначается
 или строчными буквами латинского
алфавита со стрелкой сверху:
или строчными буквами латинского
алфавита со стрелкой сверху:
 ,
…
,
…
Длина
отрезка АВ
называется длиной
или модулем вектора
и обозначается:
 .
.
Если
точки А
и В
совпадают, то вектор называется нулевым.
Нулевой вектор обозначается
либо
 ,
либо 0.
Нулевой вектор не имеет направления и
длина его равна нулю.
,
либо 0.
Нулевой вектор не имеет направления и
длина его равна нулю.
Два вектора называются коллинеарными, если они лежат на одной прямой или параллельны одной прямой (лежат на параллельных прямых).
Два вектора называется равными, если они коллинеарны, имеют одинаковое направление и длину.
Произведением
 вектора
вектора
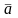 на действительное число
на действительное число
 называется новый вектор
называется новый вектор
 ,
который обладает свойствами:
,
который обладает свойствами:
1о
 ;
;
2 °
направление вектора
совпадает с направлением вектора
,
если
°
направление вектора
совпадает с направлением вектора
,
если
 (рис. 2.1, а) и противоположно направлению
вектора
,
если
(рис. 2.1, а) и противоположно направлению
вектора
,
если
 (рис.
2.1, б).
(рис.
2.1, б).
Если
точка А
является началом вектора
,
то говорят что вектор
отложен от точки А.
Отложим от точки А
вектор
,
равный
.
Затем от точки В
отложим вектор
 ,
равный
.
Вектор
,
равный
.
Вектор
 ,
равный
,
равный
 ,
называется суммой
векторов
и
и обозначается:
,
называется суммой
векторов
и
и обозначается:

Д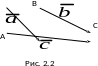 ля
любых трех точек А,
В,
С
(рис.
2.2) справедливо равенство (правило
треугольника):
ля
любых трех точек А,
В,
С
(рис.
2.2) справедливо равенство (правило
треугольника):
 .
.
Умножение вектора на число и сложение векторов называются линейными операциями над векторами.
Два
вектора называются противоположными,
если их длины равны, и они противоположно
направлены. Из определения произведения
вектора на число следует, что
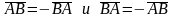 .
.
Разностью
векторов
 называется вектор
,
сумма которого с вектором
равна вектору
.
Обозначается:
называется вектор
,
сумма которого с вектором
равна вектору
.
Обозначается:
 Разность векторов можно определить
также равенством:
Разность векторов можно определить
также равенством:
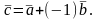 Множество всех векторов на плоскости
(в пространстве) образуют линейное
пространство.
Множество всех векторов на плоскости
(в пространстве) образуют линейное
пространство.
2.2. Проекция вектора на ось. Свойства проекций.
Единичный
вектор
 ,
направление которого совпадает с
направлением оси 0u,
называется направляющим
вектором
этой оси или ортом
оси. Если
,
направление которого совпадает с
направлением оси 0u,
называется направляющим
вектором
этой оси или ортом
оси. Если
 – единичный вектор, сонаправленный с
вектором
,
то
– единичный вектор, сонаправленный с
вектором
,
то
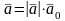 ,
если
направлен противоположно вектору
,
то
,
если
направлен противоположно вектору
,
то
 .
.
