
- •История становления и развития эконометрики
- •Парная линейная регрессия и корреляция в эконометрических исследованиях
- •Оценка значимости параметров уравнения регрессии
- •3.1. Анализ составляющих временного ряда
- •3.2. Определение наличия тренда временного ряда
- •3.4. Оценка адекватности трендовых моделей
- •Исследование временных рядов на основе моделей множественной регрессии
- •Примеры постановки и решения прикладных задач по теме «Многомерный корреляционно-регрессионный анализ»
- •Примеры для самостоятельного решения
- •Библиографический список Основная литература
- •Дополнительная литература
- •Перечень терминов и определений
- •Общие сведения
История становления и развития эконометрики
Парная линейная регрессия и корреляция в эконометрических исследованиях
Наиболее широкое распространение в эконометрических исследованиях получили линейные регрессионные модели вида (2.1)
![]() ,
(2.1)
,
(2.1)
где y – результативная (зависимая) переменная (фактор-результат);
x – независимая переменная (фактор-признак);
a,b – параметры модели.
Основными этапами эконометрического исследования являются следующие:
выбор формы уравнения взаимосвязи исследуемых факторов;
определение параметров уравнения регрессии;
оценка тесноты взаимосвязи (корреляции) исследуемых факторов;
оценка адекватности (статистической значимости) уравнения регрессии;
оценка статистической значимости параметров уравнения регрессии.
Кроме указанных этапов, прикладные исследования могут включать этапы, связанные с проведением аналитического прогноза единичных значений результативной переменной, а также оценкой точности и достоверности прогноза.
Параметры
регрессионной модели, как правило,
оцениваются методом наименьших квадратов
(МНК), суть которого заключается в том,
что сумма квадратов отклонения фактических
значений результативного признака (yi)
от соответствующих теоретических
значений (![]() ),
полученных на основе выбранной модели,
должна быть минимальной:
),
полученных на основе выбранной модели,
должна быть минимальной:
![]() .
(2.2)
.
(2.2)
В данном случае на основе МНК образуется система нормальных уравнений, решая которую получают значения параметров отобранных регрессионных моделей. Так, для линейной регрессии ( ) система нормальных уравнений имеет вид (2.3):
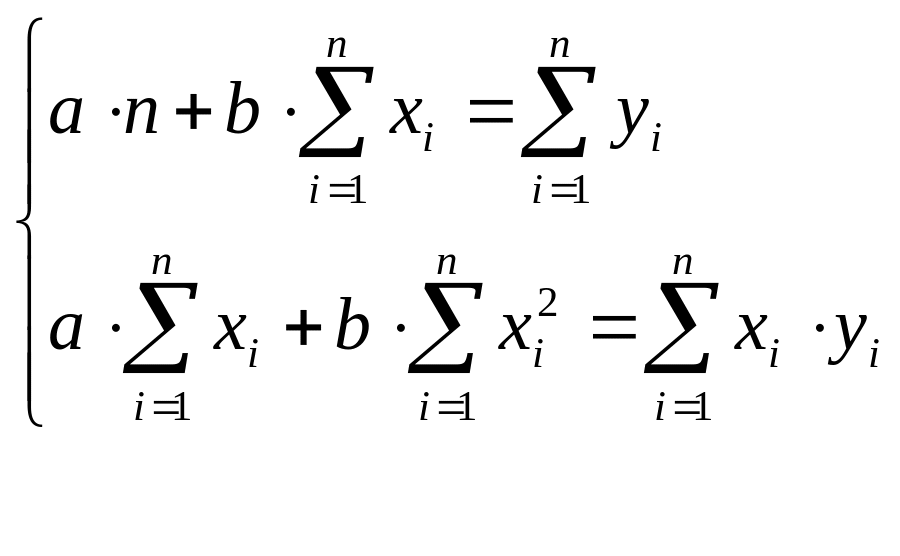 (2.3)
(2.3)
После очевидных и несложных преобразований окончательные выражения для определения параметров линейной регрессии имеют вид:
![]() (2.4)
(2.4)
![]() (2.5)
(2.5)
где
![]() - среднее значение произведения факторов
x
и y;
- среднее значение произведения факторов
x
и y;
![]() - среднее значение
фактора x;
- среднее значение
фактора x;
![]() - среднее значение
фактора y;
- среднее значение
фактора y;
![]() - среднее значение
фактора x2;
- среднее значение
фактора x2;
![]() -
квадрат среднего значения фактора x;
-
квадрат среднего значения фактора x;
![]() - среднее
квадратическое отклонение фактора x;
- среднее
квадратическое отклонение фактора x;
![]() - среднее
квадратическое отклонение фактора y.
- среднее
квадратическое отклонение фактора y.
Параметр b называется коэффициентом регрессии. Его величина показывает среднее изменение результата с изменением фактора-признака на одну единицу. Кроме того, в ряде случаев для удобства интерпретации параметра b используют коэффициент эластичности. Он показывает средние изменения результативного признака (в %) при изменении факторного признака на 1% и вычисляется по следующей формуле:
![]() .
(2.7)
.
(2.7)
Параметр a может не иметь экономического смысла. Формально параметр a – значение фактора y при x=0. Если фактор-признак x не имеет и не может иметь нулевого значения, то вышеуказанная трактовка параметра a не имеет смысла. Попытки экономически интерпретировать параметр a могут привести к абсурду, особенно при a < 0. Интерпретировать можно лишь знак при параметре a. Если a > 0, то относительное изменение результата происходит медленнее, чем изменение фактора x.
Выражения для нахождения линейного коэффициента корреляции:
![]() (2.8)
(2.8)
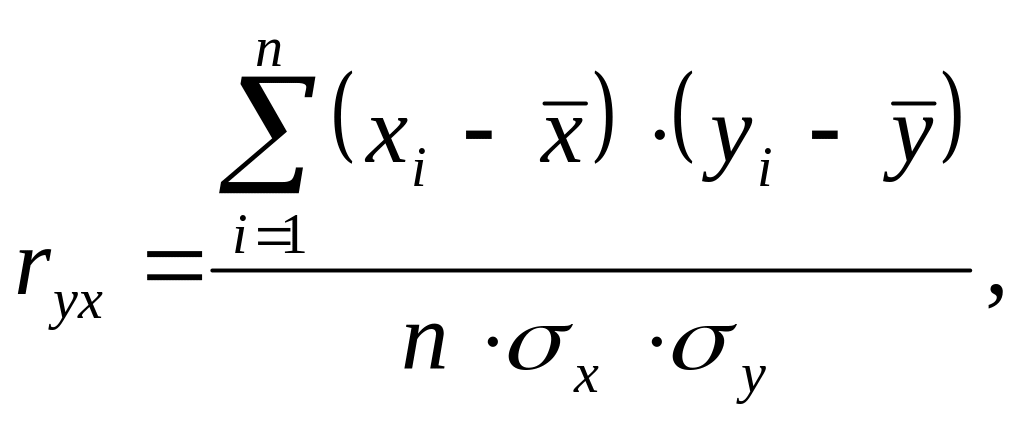 (2.9)
(2.9)
![]() (2.10)
(2.10)
где n - размерность исследуемой выборки (количество наблюдений).
Величина коэффициента
корреляции находится в пределах:
![]() и может принимать следующие значения:
и может принимать следующие значения:
если значение
![]() ,
то корреляция между исследуемыми
факторами отсутствует (факторы
некоррелированы);
,
то корреляция между исследуемыми
факторами отсутствует (факторы
некоррелированы);
если значение
![]() находится в пределах (0…0,3], то между
исследуемыми факторами имеется слабая
связь;
находится в пределах (0…0,3], то между
исследуемыми факторами имеется слабая
связь;
если значение находится в пределах (0,3…0,5], то между исследуемыми факторами имеется умеренная связь;
если значение находится в пределах (0,5…0,7], то между исследуемыми факторами имеется довольно устойчивая статистическая связь;
если значение > 0,7 , то между исследуемыми факторами имеется сильная связь (статистически значимая связь, факторы сильно коррелированны);
если значение = 1, то между исследуемыми факторами имеется функциональная зависимость.
Оценка адекватности формы регрессионной модели может быть проведена с помощью:
среднего коэффициента аппроксимации (Ā);
критерия Фишера;
коэффициента детерминации (R2).
Оценку адекватности регрессионной модели на основе среднего коэффициента аппроксимации используют следующее выражение (среднюю относительную погрешность):
![]() ,
(2.11)
,
(2.11)
Уравнение регрессии считается адекватным (точным, статистически значимым), если значение среднего коэффициента аппроксимации не превышает 8…10%.
Наиболее полно и точно проверка адекватности регрессионных моделей проводится с помощью критерия Фишера:
если Fрасч. > Fкр, то принимается основная гипотеза (Ho), свидетельствующая о правильности выбранной формы взаимосвязи исследуемых факторов;
если Fрасч. < Fкр, то принимается альтернативная гипотеза (H1), свидетельствующая о статистической незначимости выбранной формы взаимосвязи исследуемых факторов.
Эмпирическое (расчетное) значение критерия (Fрасч.) определяется с помощью следующего выражения:
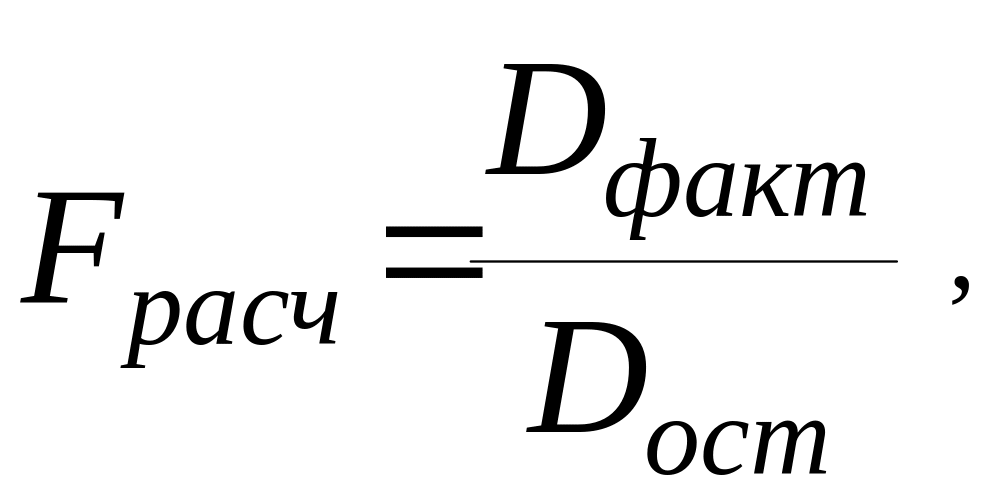 (2.12)
(2.12)
где Dфакт – дисперсия факторная (3.18);
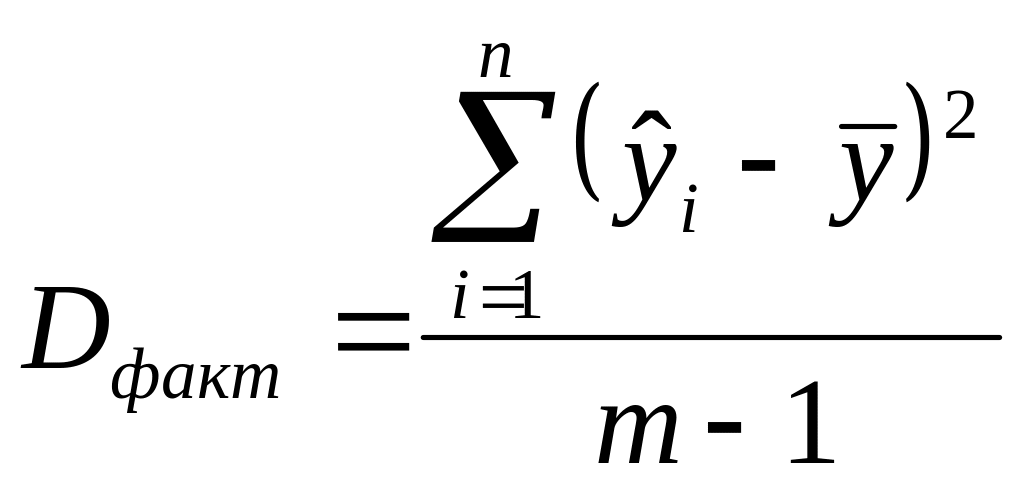 ,
(2.13)
,
(2.13)
Dост – дисперсия остаточная, определяема по выражению (2.14);
m – число параметров уравнения регрессии;
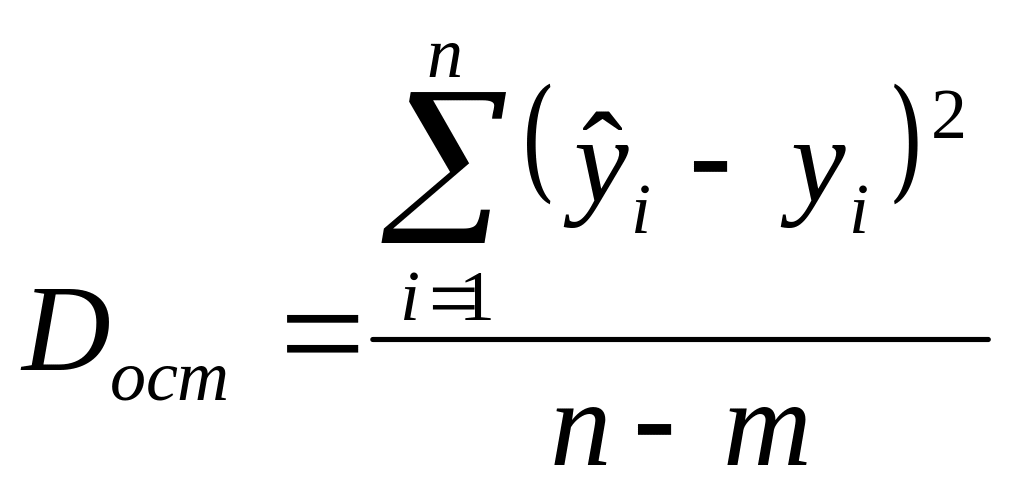 .
(2.14)
.
(2.14)
Табличное (критическое) значение критерия (Fкр.) определяется с помощью справочников или таблицам Excel (раздел мастера функций «Статистические»): Fкр=FРАСПОБР(α=1-P; ν1; ν2),
где ν1 и ν2 - степени свободы (ν1=m-1; ν2=n-m).
Сущность чисел степеней свободы (df – degrees of freedom) заключается в определении чисел свободы независимого варьирования признака, т.е указывают сколько независимых отклонений из n возможных требуется для образования данной суммы квадратов.
Процедура вычисление расчетного значения критерия Фишера тесно связана с процедурой вычисления коэффициента детерминации (R2)
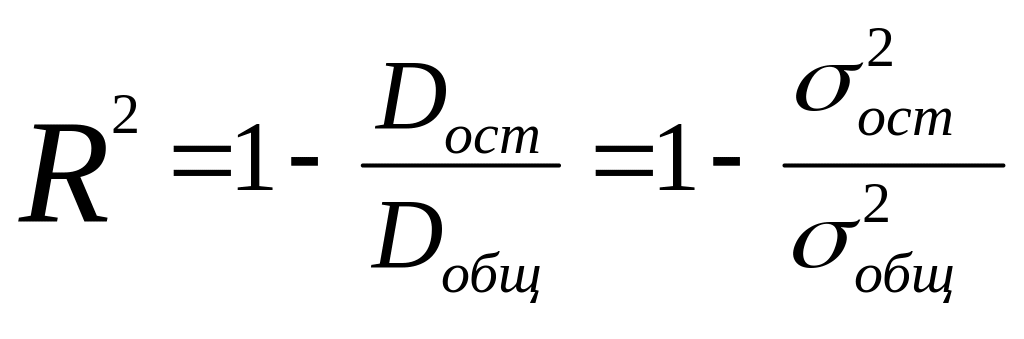 ,
(2.15)
,
(2.15)
Значение коэффициента
детерминации имеет следующие значения
R2
![]() [0; 1].
[0; 1].
Сущность коэффициента детерминации заключается в том, что он показывает зависимость вариации значений результативного признака (в %) от вариации значений фактора-признака (независимой переменной).
Иногда (при больших значениях объема выборки (n)) используют упрощенную формулу для вычисления коэффициента детерминации R2:
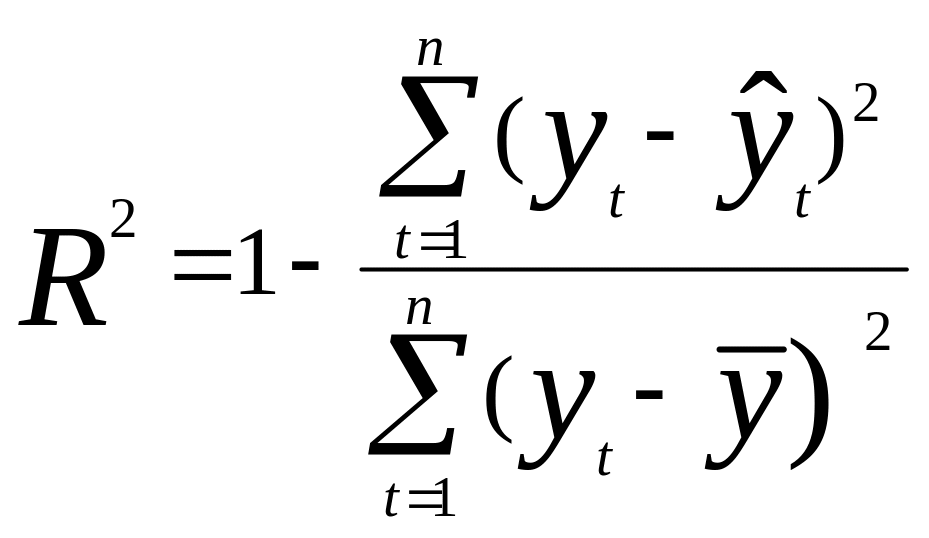 .
(2.16)
.
(2.16)
Приведенные выше выражения для вычисления коэффициента детерминации также используют при оценке тесноты взаимосвязи факторов нелинейной регрессии. Применительно к данной области эконометрических исследований для оценки тесноты взаимосвязи факторов нелинейной регрессии используется понятие корреляционного отношения (η):
![]() (2.17)
(2.17)
где Dост
- остаточная
дисперсия, определяемая из уравнения
регрессии
![]() ;
;
Dобщ - общая дисперсия результативного признака y;
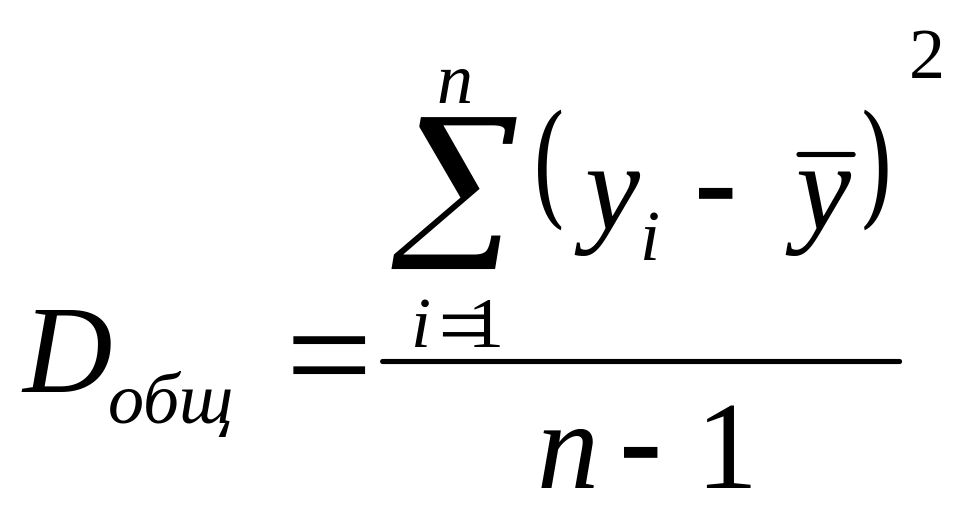 .
(2.18)
.
(2.18)
Величина показателя
η находится
в пределах:
![]() .
.
