Система з паралельними обслуговуючими пристроями та обмеженою чергою

Нехай потік вимог, які поступають в систему є пуасонівським із середньою інтенсивністю , число місць для очікування обслуговування рівне m. При переповненні черги замовлення втрачається. Вузол обслуговування складається з n паралельно розташованих обслуговуючих пристроїв.Час обслуговування замовлень на кожному з пристроїв розподілений за нормальним законом з інтенсивністю .

Можна показати, що імовірність того, що в системі перебуває k замовлень дорівнює

(5.8)

(5.9)

де (5.10)

Для відшукання імовірності p₀ простою системи використаємо умову повної сукупності подій

(5.11)

Використовуючи (5.8) і (5.9), отримаємо

(5.12)

(5.13)

Використовуючи формулу геометричної прогресії остаточно отримаєм

(5.14)

Наведені формули дають можливість встановити основні характеристики системи:

-імовірність простою системи визначається формулою (5.13)

-імовірність того, що зайнята певна кількість пристроїв визначається формулою (5.8)

-імовірність того, що зайняті всі обслуговуючі пристрої і замовлень очікують в черзі із врахуванням формули (5.9) обчислюються наступним чином

(5.15)

-імовірність втрати замовлення

(5.16)

Після деяких перетворень можна отримати середнє число пристроїв, які зайняті обслуговуванням:

(5.17)

Звідси легко знайти середнє число пристроїв, які простоюють, коефіцієнти простою та зайнятості

(5.18)

(5.19)

Відносна пропускна здатність системи (доля обслужених замовлень від загальної кількості, які поступають в систему):

(5.20)

Абсолютна пропускна здатність системи середнє число замовлень, обслужених системою за одиницю часу:

(5.21)

Можна також вивести формулу середнього числа вимог, які очікують в черзі

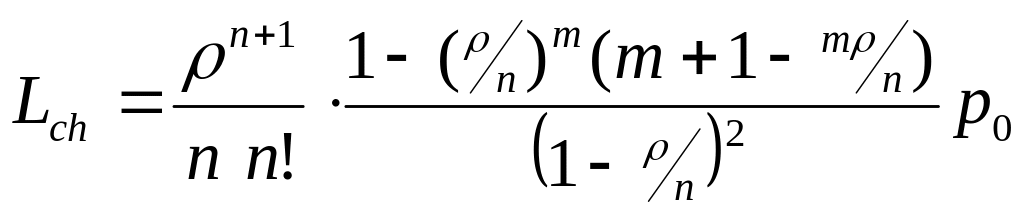(5.22)

Середнє число замовлень в системі рівне сумі середнього числа вимог в очікуванні та середнього числа вимог, які обслуговуються

(5.23)

Середній час очікування в черзі:

(5.24)

Середній час перебування замовлення в системі

(5.25)

Приклад . Підприємство розробляє нову систему контролю якості продукції. Одночасно в черзі може очікувати m виробів. Якщо при поступленні виробу всі місця очікування зайняті, то воно відвантажується без контролю. Дослідження моментів поступлення виробів на контроль показали, що вони випадкові і розподілені за законом Пуасона з інтенсивністю (1/год). Час, який затрачається на контроль одного виробу також випадковий з середнім значенням (1/год). Для значень m=3, встановити мінімальне число випробовувальних стендів, щоб було проконтрольовано не менше 95% всієї продукції, яка випускається, провести повний аналіз системи.

Розв'язання.

Згідно умов задачі . Тому .Згідно формули (5.16)

. Крім того . Будемо послідовно підставляти значення n в формулу для , аж до виконання нерівності. Для обчислення р₀ використовуєм формулу (5.14)

Обчислення оформимо у вигляді таблички

n	p0	Pvtr
1	0.0323	0.5161
2	0.0909	0.1818
3	0.1218	0.0481

Як видно із таблички необхідно встановити три випробовувальних стенди. Проведемо повний аналіз системи.

Середнє число зайнятих стендів:

Отже в середньому один стенд буде простоювати.

Коефіцієнти зайнятості та простою:

Відносна та абсолютна пропускні здатності:

Середня кількість виробів в черзі та системі:

Середній час очікування в черзі та системі