2.3. Распределения, связанные с нормальным

С нормальным или нормированным нормальным распределением тесно связано ряд распределений, широко применяемых при анализе случайных величин. Основными из таких распределений являются следующие.

2.3.1. Распределение 2 (распределение Пирсона)

Если x_i^* , i=1,2,..., - независимые нормированные нормально распределенные случайные величины с математическим ожиданием =0 и дисперсией ²=1, то сумма квадратов этих величин подчиняется распределению ² (распределению Пирсона) с числом степеней свободы . Кривые Пирсона для различных  показаны на рис. 2.5. Существуют статистические таблицы, в которых значения функции распределения Пирсона табулированы для различных уровней значимости и числа степеней свободы (табл. П.3).

Рис. 2.5. График плотности распределения Пирсона

2.3.2. Распределение Стьюдента (t - распределение)

Если U - нормированная нормально распределенная случайная величина, ² - случайная величина, имеющая распределение Пирсона с  степенями свободы, причем U и ² независимы, то величина будет подчиняться t - распределению (распределению Стьюдента). Вид кривых Стьюдента в зависимости от числа степеней свободы показан на рис. 2.6.

Рис. 2.6. График плотности распределения Стьюдента

Существуют таблицы с табулированными значениями функции t - распределения для различных уровней значимости  и различных  , а также таблицы со значениями квантилей этого распределения (табл. П.6).

Особенностью распределения Стьюдента является то, что при увеличении числа степеней свободы распределение Стьюдента приближается к нормированному нормальному распределению (распределению Гаусса). При >60 принято считать, что эти два распределения сходятся.

2.3.3. F-распределение (распределение Фишера)

Если и - две независимые случайные величины, подчиненные ² - распределению (распределение Пирсона) с числами степеней свободы _ и _ соответственно, то величина подчиняется F - распределению (распределению Фишера) с _ и _ степенями свободы. Кривые Фишера для разного числа степеней свободы _ при _ показаны на рис. 2.7. Существуют статистические таблицы как с табулированными значениями функции распределения Фишера для принятого уровня значимости, так и с табулированными значениями квантилей этого распределения (табл. П.4 и П.5).

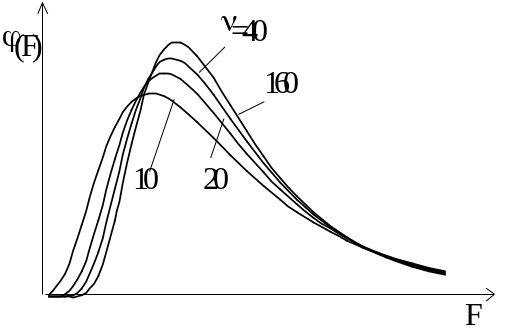
Рис. 2.7. График плотности распределения Фишера

2.4. Выборки. Статистические оценки

Для подавляющего большинства экспериментально наблюдаемых случайных величин закон распределения и его числовые характеристики (² и ) исследователю не известны и должны быть определены по опытным данным. Строго говоря, для установления точного вида закона распределения случайной величины или определения точных значений параметров распределения необходимо произвести бесконечное число измерений.

Воображаемое, бесконечно большое множество всех результатов испытаний, которые в принципе могут быть реализованы при данных условиях называют генеральной совокупностью.

По ГОСТ 15895-77, генеральная совокупность это множество всех рассматриваемых единиц.

Но порой даже сама постановка задачи проведения бесконечного (или очень большого) числа измерений выглядит абсурдно.

Например, для того чтобы точно определить закон распределения усилия осадки свинцового образца, упомянутого раньше, пришлось бы извлечь всю имеющуюся в Земле свинецсодержащую руду (или значительную ее часть), переплавить ее, превратить в образцы для лабораторных испытаний и осадить их.

На практике мы имеем возможность провести только ограниченное число измерений.

Ограниченную совокупность результатов испытаний, являющуюся частью генеральной совокупности называют выборкой (рис. 2.8), а значения характеристик, вычисляемые по выборке, называют выборочными характеристиками или оценками генеральных характеристик или статистиками.

Рис. 2.8. Генеральная совокупность (1) и выборка (2)

По ГОСТ 15895-77, выборка - это любое конечное подмножество генеральной совокупности, предназначенное для непосредственных исследований.

Вполне естественно, что найденные по данным выборки величины (выборочные числовые характеристики случайной величины) в большей или меньшей степени будут отличаться от аналогичных точных величин, так называемых генеральных характеристик, определенных по генеральной совокупности данных.

Генеральные числовые характеристики случайной величины являются детерминированными величинами, а выборочные, т.е. их оценки, - случайными. Эта разница генеральных и выборочных характеристик является принципиальной и определяет то, что величины, рассчитанные по выборке, являются некоторым приближением точных значений генеральных характеристик. Точность приближения зависит от количества испытаний N и местоположения опытных точек, поэтому говорят, что выборочные характеристики являются оценками неизвестных значений генеральных характеристик.

Смысл статистических методов заключается в том, чтобы по выборке ограниченного объема (т. е. по некоторой части генеральной совокупности) высказать обоснованное суждение о свойствах генеральной совокупности в целом.

Подобное суждение получают путем оценивания эмпирических (выборочных) аналогов вероятностных характеристик исследуемой величины, иначе говоря, путем оценивания параметров (характеристик) генеральной совокупности с помощью некоторой подходящей функции результатов наблюдений - оценок параметров распределения (обычно слова “параметров распределения” опускают).

По ГОСТ 15895-77, оценивание – это определение приближенного значения неизвестного параметра генеральной совокупности по результатам наблюдений.

По ГОСТ 15895-77, оценкой называется статистика, являющаяся основой для оценивания неизвестного параметра распределения.

Для оценивания одного и того же параметра распределения случайной величины можно использовать различные оценки, различные эмпирические, выборочные аналоги.

Пример. Пусть мы имеет некоторую выборку x₁, x₂, x₃, ... ,x_N, с соответствующими значениями 6,13; 6,00; 5,96; 5,94; 5,91; 5,75; 5,69; 5,67; 5,46; 5,30.

В качестве оценки математического ожидания могут быть рассмотрены, например, следующие величины:

среднее арифметическое ,

среднее по интервалу ,

центральный момент ,

.

Для того чтобы выбрать наилучшие из оценок, необходимо сформулировать некоторые требования к их свойствам, желательно с точки зрения практики.

Такими требованиями являются.

1. Состоятельность.

По ГОСТ 15895-77, состоятельная оценка - это оценка, сходящаяся по величине к значению оцениваемого параметра при безграничном возрастании объема выборки.

Иными словами, вероятность события, заключающегося в непревышении разницы между оценочной и генеральной характеристикам сколь угодно малой величины , при увеличении объема выборки должна неограниченно приближаться к единице .

Состоятельность оценки гарантирует исследователю увеличение точности оценивания с ростом N и то, что хотя бы в пределе при N он может получить точное значение .

2. Несмещенность.

По ГОСТ 15895-77, несмещенная оценка - оценка, математическое ожидание которой равно значению оцениваемого параметра.

Для несмещенной оценки характерно, что для любого N . Иными словами, несмещенность означает отсутствие систематической погрешности при оценивании параметров.

3. Эффективность.

По ГОСТ 15895-77, эффективная оценка это несмещенная оценка, имеющая наименьшую дисперсию из всех возможных несмещенных оценок данного параметра.

Эффективная оценка, следовательно, имеет минимальную случайную ошибку и в этом смысле наиболее точная.

В приведенном выше примере состоятельной, несмещенной и эффективной оценкой является среднее арифметическое