Понятие вероятности

Попытаемся определить понятие вероятности, которое интуитивно вроде бы ясно. Существуют три подхода к определению вероятности: классический, статистический, аксиоматический.

Классический подход к определению вероятности.

При классическом подходе рассматривается полная группа попарно несовместных равновозможных элементарных исходов.

Испытание: вытаскивание из урны, в которой лежат белые и красные шары, одного шара

Элементарный исходы: 1) шар белый; 2) шар красный

 Испытание: бросание 2 костей.

Элементарные исходы:

1 ая кость 2 ая кость

n очков m очков

Всего 36 исходов.

Обозначим элементарные исходы

Событие А: сумма очков на двух костях = 4.

Элементарные исходы: , ,

Событию А благоприятствуют 3 элементарных исхода.

Событие В: сумма очков на двух костях <= 4.

Элементарные исходы: , ,

, ,

Событию В благоприятствуют 6 элементарных исходов.

Интуитивно понятно, что событие В более вероятно, чем А.

Вероятностью события А называется отношение числа благоприятствующих этому событию исходов к общему числу элементарных исходов :

P(A)= .

Свойства вероятности

1.Если А - достоверное Р(А)= 1 ; т.к. m= n

2. Если А – невозможное Р(А)= 0; т.к. m=0

3. Вероятность любого события А 0 Р(A) всегда, т.к. 0 .

Недостатки классического определения:

1. Требование конечного (в крайнем случае - счетного) числа элементарных исходов.

2. Требование симметрии опыта, т.е. равновозможности исходов.

Первый недостаток преодолевается путем введения геометрической вероятности.

Пусть на плоскости имеется область Q, в ней содержится подобласть .

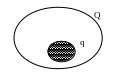В область Q наудачу бросается точка. Наудачу здесь значит, что брошенная точка может попасть в любую точку области Q; вероятность попадания в какую-либо часть области q пропорциональна площади этой фигуры и не зависит от ее формы и расположения внутри большой области. Вопрос: какова вероятность события А - что точка попадет в область q?

P(A)= - отношение площадей.

 Q – круг радиусом 10см, q – круг радиусом 5см, P(A)=

Определение геометрической вероятности обобщается на любую меру области (отрезок, объем и т.д.). Обозначив меру как mes, получим

Р(А)

Таким образом, введением геометрической вероятности мы избавились от счетности (и, тем более, конечности) элементарных исходов. Но – увы!-требование равновозможности исходов никуда не делось.

Статистический подход к определению вероятности.

В задачах технического или естественнонаучного характера требование равновозможности исходов выполняется крайне редко. Классическим путем нельзя вывести вероятность распада атома радия за определенный период времени или определить вероятность рождения близнецов.

Пусть проводится серия из n опытов, в каждом из которых может случиться или не случиться событие А.

Относительной частотой называется отношение количества событий, где А произошло , к общему числу опытов :

Понятие частоты является основным при экспериментальном изучении случайных событий. Частота не может служить объективной характеристикой изучаемого случайного события, так как зависит от случайного стечения обстоятельств, связанных с данной серией испытаний, от индивидуальных особенностей самого экспериментатора.

Однако с увеличением числа испытаний частота становится «устойчивой». Теория вероятностей предназначена для описания случайных событий, обладающих устойчивой частотой. Вероятность случайного события соответствует в идеализированном виде тому пределу, к которому стремится устойчивая частота события при неограниченном увеличении числа испытаний.

Свойства вероятности, вытекающие из классического определения, сохраняются и при статистическом определении вероятности

1. Если А - достоверное = 1 ; т.к. m= n

2. Если А – невозможное = 0; т.к. m=0

3. Вероятность любого события А 0 всегда, т.к. 0 .

Недостатки статистического определения вероятности: необходимо приводить большое (и, неизвестно насколько большое) число испытаний.

В чем принципиальная разница классического и статистического подходов? Классическую вероятность можно вычислить до испытания, да и самогоиспытания можно не проводить. Относительную частоту можно вычислить только после проведения испытания. ( до того и после того)

Соответствие между классическим и статистическим определениями было выявлено еще в период становления теории вероятностей как теории азартных игр. Было установлено, что при корректном использовании классического определения вероятность событий практически совпадает с их частотами при большом числе повторений эксперимента.

  Есть кости и час времени. Нужно установить, нет ли свинца в шестерке. Как?