2. Закони збереження та їх зв’язок з фундаментальними властивостями простору і час

Закон збереження імпульсу: геометрична сума імпульсів тіл, які складають замкнену систему, є величина стала: m1v1 + …+ mnvn = const . Закон можна застосувати і для системи тіл, на які дія зовнішніх сил є скомпенсованою.

Закон збереження енергії: енергія не виникає і не зни­кає, вона тільки перетворюється із одного виду в інший і передається від одного тіла до іншого в рівних кіль­костях.

Закон збереження моменту імпульсу стверджує, що момент кількості руху у замкненій системі зберігається під час еволюції цієї системи з часом. Момент імпульсу замкнутої системи тіл залишається незмінним при будь-яких взаємодіях тіл системи. Закон збереження кількості руху є наслідком ізотропності простору.

Найпростіше закон збереження імпульсу формулюється й доводиться в Лагранжевій механіці. Ізотропність простору значить, що функція Лагранжа L не залежить від вибору системи координат. Виберемо будь-яку вісь й візьмемо за узагальнену координату кут повороту навколо цієї осі. Незалежність функції Лагранжа від цього кута означає

тобто момент сили дорівнює нулю. Тоді, Згідно з рівнянням Лагранжа

тобто часова похідна від моменту імпульсу дорівнює нулю. Сам момент імпульсу тоді є інтегралом руху.

Закон збереження маси — закон, що постулює збереження сумарної маси всіх речовин у замкненій системі, не зважаючи на будь-які внутрішні процеси. Цей закон працює лише у класичній фізиці, коли релятивістські ефекти невеликі.

Зако́н збере́ження електри́чного заря́ду — один із фундаментальних законів фізики. Він полягає в тому, що повний заряд (алгебраїчна сума зарядів) ізольованої замкнутої фізичної системи тіл залишається незмінним при будь-яких процесах, які відбуваються всередині цієї системи. Для неізольованих систем закон збереження заряду набирає вигляду рівняння неперервності

де - густина заряду, - густина струму. Це математичний запис твердження, що зміна густини заряду в достатньо малому об'ємі дорівнює потоку заряду через поверхню цього об'єму (в диференційній формі).

3. Динаміка поступального і обертального руху твердого тіла

Розглядаючи рух твердого тіла, розрізняють поступальний і обертальний рухи. Поступальним рухом твердого тіла називають такий його рух, при якому будь-яка пряма, проведена в тілі, залишається паралельною самій собі.

Обертальним рухом твердого тіла називають такий його рух, при якому всі точки, з яких складається тіло, описують кола, що лежать у паралельних площинах, а геометричне місце центрів цих кіл утворює пряму, яку називають віссю обертання.

Розглянемо поступальний і обертальний рухи абсолютно твердого тіла.

Поступальний рух абсолютно твердого тіла можна описати рухом окремої його точки. Як зазначалося в підрозділі 1.1, абсолютно твердим називають тіло, яке не змінює своєї форми при будь-яких діях. Інакше кажучи, відстань між будь-якими точками абсолютно твердого тіла залишиться сталою за всіх умов. Звичайно, таких тіл у природі не існує. Це поняття є зручною ідеалізацією, справедливою лише тоді, коли можна нехтувати деформацією тіл.

Якщо абсолютно тверде тіло переміщується поступально зі швидкістю υ, то й будь-яка його точка матиме таку саму швидкість. Умовно поділимо тіло А на n частин і знайдемо його кінетичну енергію як суму кінетичних енергій його частин:

де М — маса тіла; m_і — маса його і-ї частини.

Отже, кінетичну енергію твердого тіла, яке поступально рухається, можна визначити з формули, аналогічної формулі для кінетичної енергії матеріальної точки.

Якщо тверде тіло обертається навколо осі з кутовою швидкістю ω, то лінійна швидкість окремих точок збільшуватиметься зі збільшенням відстані від осі обертання відповідно до формули (1.21). Підставивши (1.21) в (2.50), дістанемо

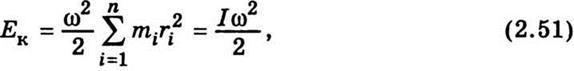
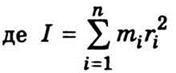— момент інерції тіла.

Момент інерції будь-якого тіла є фізичною величиною, яка враховує масу і її просторове розміщення відносно осі обертання. Моментом інерції матеріальної точки називають добуток маси точки на квадрат відстані її від осі обертання:

Для довільного тіла

Скориставшись формулою (2.53), можна визначити моменти інерції різних тіл. Наприклад, момент інерції тонкого кільця відносно геометричної осі І = mr², диска І = mr²/2, кулі І = =2mr²/5 тощо.

Розглянемо тіло, яке обертається з кутовою швидкістю ω (рис. 2.9) і під дією сили F, що прикладена до точки А на відстані r від осі обертання. Через проміжок часу dt тіло з точки А переміститься в точку А', а радіус-вектор точки переміститься на кут dφ, який зв’язаний з кутовою швидкістю (dω = ωdt). При цьому точка А описуватиме дугу ds(ds = rdφ).

Рис. 2.9

Виходячи із загального визначення роботи (2.38), для цього випадку запишемо

Ця робота йде на зміну кінетичної енергії обертання 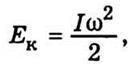тому можна записати

Після перетворень дістанемо

де М = Fr — момент сили. Врахувавши це, із (2.55) дістанемо

якщо I = const, і

якщо І ≠ const.

Добуток моменту інерції на кутову швидкість називають моментом імпульсу. Вираз (2.56) називають основним рівнянням динаміки обертального руху твердого тіла. Запишемо його так:

Якщо на систему не діють зовнішні сили або рівнодійна їх не створює моменту сил відносно осі обертання, то М = 0 і вираз (2.57) набере такого вигляду:

Отже, якщо на систему не діють моменти зовнішніх сил, то момент імпульсу її залишається сталим. Це закон збереження моменту імпульсу.

Наведемо приклади, що ілюструють закон збереження моменту імпульсу. Кулька утримується на нитці, що намотується на палку. Із зменшенням довжини нитки зменшується момент інерції кульки і, отже, збільшується кутова швидкість. Гімнаст під час стрибка через голову притискує до тулуба руки й ноги. Цим він зменшує свій момент інерції, а оскільки добуток Iω має залишатися незмінним, то кутова швидкість обертання ω збільшується, і за короткий проміжок часу, поки гімнаст перебуває в повітрі, він робить повний оберт, а то й кілька.