Өзара перпендикуляр күштердің әсерінен тікбұрышты параллелепипедтің деформациясы.

1. Біртекті изотропты дене тікбұрышты параллелепипед формалы болсын дейік, оның қарама-қарсы беттеріне осы беттерге нормаль күштері әсер етсін. Сәйкес созушы кернеулерді деп белгілейік.Осы күштердің әсерінен пайда болатын деформацияларды анықтвайық . Деформацияларды кіші болады деп аламыз. Осындай жағдайда ғана біз кіші деформациялардың суперпозициясын қолдана аламыз.

Координата осьтерін параллелепипед қырларына параллель бағыттаймыз. X,Y,Z –осы қырлардың ұзындықтары болсын. Егер тек F_x күші әсер етсе, онда х қыры өрнегімен анықталатын ұзаруын алатын еді . Егер тек Ғ_у күші әсер етсе, онда у осьіне перпендикуляр параллелепипед өлшемдері кішкрейген болар еді. Сәйкесінше, х қыры формуласы арқылы анықталатын теріс таңбалы өзгеріс алады.Соңында ,х қырының салыстырмалы өзгерісі Ғ_z күші әсерінен те ң болады. Егер барлық күштер бірдей әсер етсе, онда суперпозиция принципі бойынша х қырының қорытқы ұзаруы тең болады. Параллелепипедтің у,z бағыттары бойынша ұзаруды есептеу де осыған ұқсас. Нәтижесінде параллелепипедтің барлық үш қырының ұзаруын мына түрде жазуға болады:

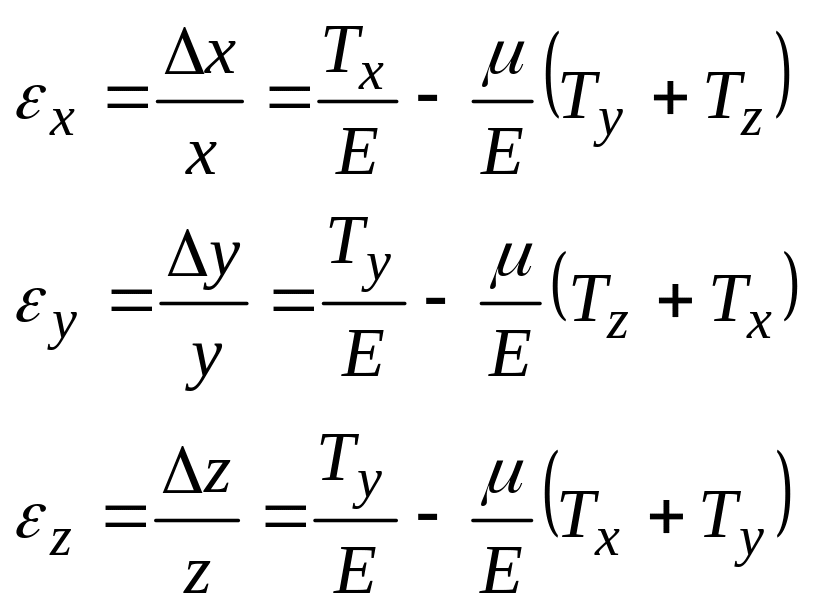
2.Параллелепипедтің х осі бойынша квазистатикалық созылуы кезінде тең жұмыс жасалады, мұндағы -x осіне перпендикуляр беттің ауданы. Бұл жұмысты мына түрде өрнектеуге болады

мұндағы V=xyz –параллелепипед көлемі . У және Z координаттары бағытындағы квазистатикалық созылуы кезіндегі жұмыс осыған ұқсас болады.Бұл жұмыстарды бір-біріне қосып және оны параллелепипед көлеміне бөлсек қарастырылып отырған жағдайдағы серпімді энергияның тығыздығы үшін келесі өрнекті аламыз:

теңдіктері арқылы бұл өрнекті мына түрде жазуға

болады:

Егер ТхTyTz созушы кернеулердің тек біреуі ғана нөлден өзгеше болса,онда бұл формулалар қарапайым түрдегі формулаларға көшеді.

Жалпы жағдайда формула көрсеткендей,серпімді энергия тығыздығы ТхTyTz шамаларының біртекті квадраттық функциясы болып табылады. Берілген созушы кернеуде (немесе қысымда) ол серпімділік модуліне Е кері пропорционал. Серіппе қаншалық қатаң болса, тұрақты созушы кернеудің серпімді энергиясы соншалық аз болады. Идеалды қатты денелер қандай созушы кернеу және қысым әсер етсе де ешқандай серпімді энергияға ие болмайды.

ТхTyTz созушы кернеулер

формуласы көрсеткендей, арқылы сызықты өрнектеледі.

Лекция №5

Жан-жақты және бір жақты созылу мен сығылу.

Дербес жағдайды қарастырамыз, барлығы тең және теріс болатын кеулерді алайық. Бұл жағдайда параллелепипедке жан-жақтан тұрақты қысым әсер етеді.

Үш салыстырмалы деформациялар бір-бірімен тең және мына өрнекпен сипатталады:

(1)

Бұларды папаллелепипедтің деформациялануы кезіндегі көлемнің салыстырмалы өзгеруі арқылы табу оңай.

Шынында да, теңдігінің екі жағынан да логарифмдік туынды алып, мынаған келеміз:

Немесе

(2)

Сондықтан (1) -формуланы мына түрге келтіреміз:

(3)

Мұндағы К тұрақтысы мына өрнекпен анықталады:

(4)

Бұл тұрақты жан-жақты сығылу модулі деп аталады.

(3) -формула тек қана тік бұрышты формалы денелерге ғана емес, сонымен қатар кез келген формалы денелерге де арналған. Мұны дәлелдеу үшін кез келген денені тікбұрышты параллелепипед формалы бөлшектерге ойша бөліп байқауға болады. Бұл бөлшектерге тұрақты қысым әсер етеді. Олардың көлемінің салыстырмалы өзгеруі, сонымен қатар тұтас дененің салыстырмалы өзгеруі бірдей болады және (3)-формуламен анықталады.

Жан-жақты сығылу деформациясы кезінде серпімді энергияның тығыздығы:

(5)

U өлшемі оң болғандықтан, болуы керек, яғни

(6)

Енді бір жақты созылу немесе сығылуды қарастырайық.

Стержень өзінің өсі бағытында (х координата өсі) еркін созыла және сығыла алсын, ал оның көлденең өлшемдері өзгере алмайды. Бұл жағдай шексіз серпімді ортадағы көлденең тлоқындардың таралу теориясыда зор мағынаға ие. Ортаның толқынның таралу бағытындағы стержень формалы бөлшегін ойша бөліп аламыз. Мұндай «стержень» көлденең бағытта сығыла да, созыла да алады. Бірақ оның көлденең өлшемдерінің өзгеруіне қоршаған орта кедергі болады.

Стерженнің көлденең қимасының формасын есептемеуге болады.

Көлденең қимасы тікбұрышты болып келетін стержень алайық. Стержень арқылы тұрақты керу әсер етсін. көлденең кернеулері Y және X бағытындағы стерженнің өлшемдерінің өзгермеу шартынан табылады. деп алып, мынаны аламыз:

Осы жерден мына өрнек табылады:

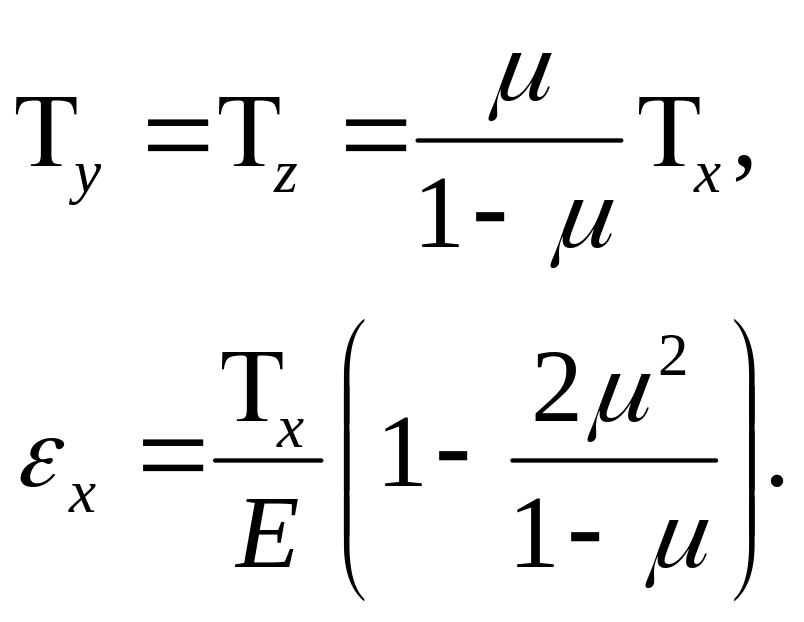(7),(8)

Орнына мынаны енгіземіз:

(9)

Немесе

(10)

Сонда мынау шығады екен:

(11)

тұрақтысы бір жақты созылу модулі деп аталады.

Лекция №6

Ығысу.

Біртекті изатропты заттан жасалған кубты алайық.Оның АД және ВС қарамаө қарсы қырларына өзара тең және қарама-қарсы бағытталған жанама күштер түсірейік. Бұл жұп күштердің әсерінен куб айнала бастайды.Айналуды тоқтату үшін АВ және СД қырларына тура осындай жанама қүштер түсірейік. Бұл кезде куб айналмайды, тек деформацияланады. Бұл тәрбиеәжірбиеде түсірілген кенеудің әсерңінен АВСД квадраты А'В'С'Д' ромбысына айналады. Бұл жағдайда АС диогональі ұзарады, алВД диогональі қысқарады. Ал көлем өзгеріссіз қалады, көлемнің өзгерісі АС және ВД диогональдарының өзгерісімен салыстырғанда өте аз, сондықтан оларды ескермеуге болады. Сондай-ақ квадрат қырларының өзгерісі өте аз, сондықтан деформациядан соң жаңа А'Д' алдыңғы АД табанына келетіндей етіп бұруға болады. Бұл жерден біз қарастырып отырған деформация кубтың барлық АД табанына паралель бағытта және осы табанға парлель бағытта ығысады. Сондықтан бұл деформация ығысу деп аталады. Ығысу шамасы ығысқан қабатпен АД табанына дейінгі арақашықтыққа пропорционал. АВ жәнеАВ' арасындағы бұрыш

Ығысу бұрышы деп аталады.Егер бұрыш болса, онда осы ығысу деформациясы үшін мына өрнекті жаза аламыз.

мұндағы -жанама кернеу. -ығысу модулі сиақты тұрақты, ол дененің материалына тәрбиеәуелді.

Енді ығысу деформациясы үшін серпімді энергианың тығыздығын анықтайық. Осы кубтың кез келген беттік -ке ығыстыру үшін мына жұмыс жасалады.

-осы беттің ауданы.

Егер кубтың қабаттарын -деп белгілесек онда,

осыдан,

Бұдан серпімді энергианың тығыздығы мынаған тең.

Лекция №7