Өлшемдік теориясын пайдалану

«Бірліктер жүйесі» термині екі мағынада қолданылады. Кең мағынады бірліктер жүйесі негізгі шамалыр мен формулаларды сипаттайды, ал негізгі шаманың масштабтары бекітілмейді. Бұған мысалы LMT жүйесін қарастырсақ болады, яғни ұзындық, масса және уақыт. Бұдан да басқа мысалдарға жататын электротехникалық жүйесі де, яғни LMTI болып табылады. Мұндағы негізгі шамалар ұзындық, масса, уақыт және электр тогының күші. Бірліктер жүйесі тар мағынада қосымша белгілі таңдалған негізгі бірліктердің масштабтарын сипаттайды. Бұған мысал ретінде СГС және МКСА жүйесі жатады.

Бірінші жағдайда LMT жүйесіндегі ұзындық, маса және уақыт үшін олардың өлшемі бірлігі ретінде сантиметр, грамм және секукннд қабылданған.

Екінші жағдайда LMTI жүйесіндегі ұзындық, масса, уақыт және ток күші үшін өлшем бірлігі ретінде метр, килограмм, секунд және ампер қабылданған. Өлшемдер теориясында «бірліктер жүйесі» термині кең мағынада түсіндіріледі.

Өлшемдер түсінігі қайсыбір бірліктер жүйесінде сандық ара қатынасы әр түрлі физикалық шамалар да бір ғана формуламен шығып содан туындап отыратын шамаларға байланысты талаптан пайда болатын. Осы талапқа байланысты жалпы физикалық шамалардың «өлшемдік формулалары» анықталады.

Мысалы, бір-бірімен байланысты физикалық шамаларды қарастырайық. Қарапайым жағдайда екі ғана шамадан шектелейік, бірінші негізгі, ал екінші туынды шама болып табылады. Оның сандық мәндері х және у, у=f(х) теңдігімен байланысты.

f(х) функциясының жалпы түрін анықтайық. Егер негізгі х шамасын α рет азайтсақ, онда оның сандық мәні сонша рет көбейеді және ол мынаған тең:

Х=αх

Бұл жағдайда туынды шама у – тың бірлігі азаяды, ал оның сандық мәні β рет көбейеді және ол мынаған тең болады.

У=βу

Осы жерден Х және У сандық мәндерін х және у сандық мәндерімен байланысты болуын талап етеміз, яғни

У=f(Х) немесе βу=f(αх)

β – ны берілген деп алсақ, α – ның кез келген мәнде осы шарт қанағаттандырады.

Тапсырмада β – ны α аргументінің функциясы ретінде қарасытырамыз. Бұл сұраққа «өлшемді формула» жауап береді. Мысалы, екі физикалық шама у=f(х) қатынасымен байланысты болсын.

х және у шамалары α және β ретінде көбейткенде мынаған тең болады.

Х=αх және У=βу

х және у мәндері жаңа физикалық шама Х және У пен байланысты болу үшін, яғни У=f(Х) болу үшін, α және β сандары қандай шатрты қанағаттандыру керек деген сұраққа «ұқсастық теориясы» жауап береді. Бұл сұрақ

βу=f(αх)

теңдеуін зеттеуге алып келеді.

Ұқсастық теориясы әр түрлі физикалық шамалардың көбеюі немесе азаю модельдерін және өзгерістерін зерттейді.

Өлшемдік формуласының далпы түрін құрайық. Жоғарыдан түсінікті болғандай,

у=f(х) теңдеуінен У=f(Х) теңдеуі шығу керек, мұнда Х-тің орнына

Х=αх

У-тің орнына

У=βу

х аргументі және кез келген мәнді қабылдауы мүмкін. Тапсырамада α белгілі болғанда, β-ны табу керек болып табылады.

Дифференциялдау жолымен α және β-ны табамыз:

Бұл формуланың екінші түрін мына түрде:

Бұны Х және У-ке бөлетін болсақ α және β былайша

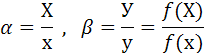
түрінде жазалады. Сонда осыдан мынаны аламыз

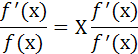
Сол жақта х функциясы, оң жақта Х функциясы тұр. Оған (F) белгілеу енгізсек:

F(х)=F(Х)

Біріқ α параметрінің Х және Х=αх аргументірі кез келген мәнді қабалдауы мүмкін. Сондықтан F(х)=F(Х) теңдігі бірдей немесе тепе-тең орныдалуы керек. Бұл жерде F(х) тұрақты. Бұл тұрақтына m деп белгілесек, дифференциялдық теңдеу аламыз:

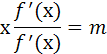
немесе

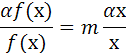
Осыдан табатынымыз

F(х)=f₀х^m

мұндағы f₀ – интегралдық тұрақты. Мұндай жағдайда

у=f₀х^m

сол сияқты

У=f₀Х^m немесе βу=f₀(αх)^m

Мұны х және у-ке бөлетін болсақ, мынау шығады:

β=α^m

осыны өлшемдік формула деп атаймыз.

Лекция №24