
- •Математика
- •Вологда
- •Утверждено редакционно-издательским советом ВоГту Составитель: Абильдин а.А., канд.Техн.Наук, доцент
- •Введение
- •Тема 1. Векторы. Линейные операции над векторами.
- •§1.1. Действия над векторами.
- •3.Скалярное произведение
- •1.3.Линейная зависимость и независимость векторов
- •Тема 2. Матрицы и определители
- •§2.2. Обратная матрица
- •Тема 3. Решение систем линейных уравнений
- •Тема 4. Произведение преобразований
- •Собственные числа и собственные векторы матрицы линейного преобразования (оператора)
- •Тема 5. Собственные векторы линейных преобразований
- •Тема 6. Комплексные числа
- •Контрольная работа № 1
- •Тема 8. Предел и непрерывность функций
- •Тема 9. Производная и дифференциал
- •Исследование функций
- •Тема 10. Приближенное решение уравнений
- •Контрольная работа №2
- •Литература
Тема 5. Собственные векторы линейных преобразований
Пусть
-
линейное преобразование. Всякий ненулевой
вектор
![]() ,
,

П ример 1.5.4.Найти собственные числа и собственные векторы матрицы линейного преобразования
Система однородных линейных алгебраических уравнений (93) для нахождения собственных векторов имеет вид
(11-λ)x1+2x2-8x3=0
2x1+(2-λ)x2+10x3=0 (1.5.7)
-8x1+10x2+(5-λ)x3=0
Вычислим определитель системы и решим соответствующее характеристическое уравнение
Характеристическое уравнение имеет вид
λ3-18 λ2-81 λ+1458=0, а его решение λ1=9, λ2=18, λ3=-9. Найденные значения λi,
![]() подставим
(1,5)
подставим
(1,5)
Решение этой системы х1= С(2,2,1)Т, С єR, а соответствующий единичный вектор х01 =(2/3, 2/3, 1/3) Т
При λ 2=18: х02=(-2/3, 1/3, 2/3)Т , при λ3=-9: х03 =(1/3, -2/3, 2/3)
Тема 6. Комплексные числа
Комплексными
называются числа вида z=x+iy,
где x
и y-действительные
числа, а i2
=-1. Число x
называется действительной частью
комплексного числа z,
а число y
– коэффициент при i
– мнимой частью. Число
![]() =x-iy
называется сопряженным к числу z=x+iy.
У сопряженных чисел равны действительные
части, а мнимые отличаются только знаком.
Числу z
можно сопоставить вектор, направленный
из начала O
в точку z.
Модуль
=x-iy
называется сопряженным к числу z=x+iy.
У сопряженных чисел равны действительные
части, а мнимые отличаются только знаком.
Числу z
можно сопоставить вектор, направленный
из начала O
в точку z.
Модуль
![]() комплексного числа z
вычисляется по формуле
комплексного числа z
вычисляется по формуле
![]() .
.
Угол образованный радиусом-вектором Oz (рис.1) с положительным направлением действительной оси Оx, называется аргументом числа z и обозначается Argz.
Любое
комплексное число z
можно представить в алгебраической
форме z
= x + iy
и в тригонометрической форме z=
r
(cos
+isin).
Здесь
![]() ,
=Аrgz
-, причем различные значения аргумента
отличаются на 2
,
=Аrgz
-, причем различные значения аргумента
отличаются на 2![]() k
k![]() ,
где к
- целое число. Под главным значением
аргумента понимается значение ,
удовлетворяющее условию -
.
Таким образом Аrgz
= аrgz+2
к.
,
где к
- целое число. Под главным значением
аргумента понимается значение ,
удовлетворяющее условию -
.
Таким образом Аrgz
= аrgz+2
к.
Комплексные числа z еще можно представить в показательной форме z =rеi, где r и - то, что и в тригонометрической форме.
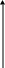 y
y
z


r

![]()
 o
o
![]() x
x
Рис.2
Пример
Найти
корни уравнения
![]() .
.
Решение.
Находим
модуль и аргумент числа
![]()
![]()
![]()
 .
.
Тогда корни данного уравнения определяем по формулам
![]() ,
к = 0,1,2, т.е. уравнение имеет три корня:
,
к = 0,1,2, т.е. уравнение имеет три корня:
![]() ,
при к=0;
,
при к=0;
 ,
при к=1;
,
при к=1;
 ,
при к=2
,
при к=2
или
![]()
![]()
![]()
Контрольная работа № 1
Задание 1. Решить систему уравнений методом Гаусса и с помощью обратной матрицы
1. ![]()
2. ![]()
3. ![]()
4. ![]()
5. ![]()
6. ![]()
7. ![]()
8. ![]()
9. ![]()
10. ![]()
11. ![]()
12. ![]()
13. ![]()
14. ![]()
15. ![]()
6. ![]()
17. ![]()
18. ![]()
19. ![]()
20. ![]()
21.
![]()
22. ![]()
23. ![]()
28.
![]()
24.
![]()
25. ![]()
26. ![]()
27. ![]()
29.
![]()
30.
![]()
Задание 2.
В
задачах 1-30 даны два линейных преобразования.
Средствами матричного исчисления найти
преобразование, выражающее X"=![]() через X=
через X=![]()
1.
![]()
![]()
2.
![]()
![]()
3.
![]()
![]()
4.
![]()
![]()
5.
![]()
6.
![]()
![]()
7.
![]()
![]()
8.
![]()
![]()
9.
![]()
![]()
10.
![]()
![]()
11.
![]()
![]()
12.
![]()
![]()
13.![]()
![]()
14.
![]()
![]()
15.
![]()
![]()
16.
![]()
![]()
17.
![]()
![]()
18.![]()
![]()
19.![]()
![]()
20.
![]()
![]()
21.
![]()
![]()
22.
![]()
![]()
23.
![]()
![]()
24.![]()
![]()
25.
![]()
![]()
26.
![]()
![]()
27.
![]()
![]()
28.
![]()
![]()
29.
![]()
![]()
30.
![]()
![]()
Задание 3.
Найти собственные векторы и собственные значения линейного преобразования, заданного в некотором базисе матрицей.
1.
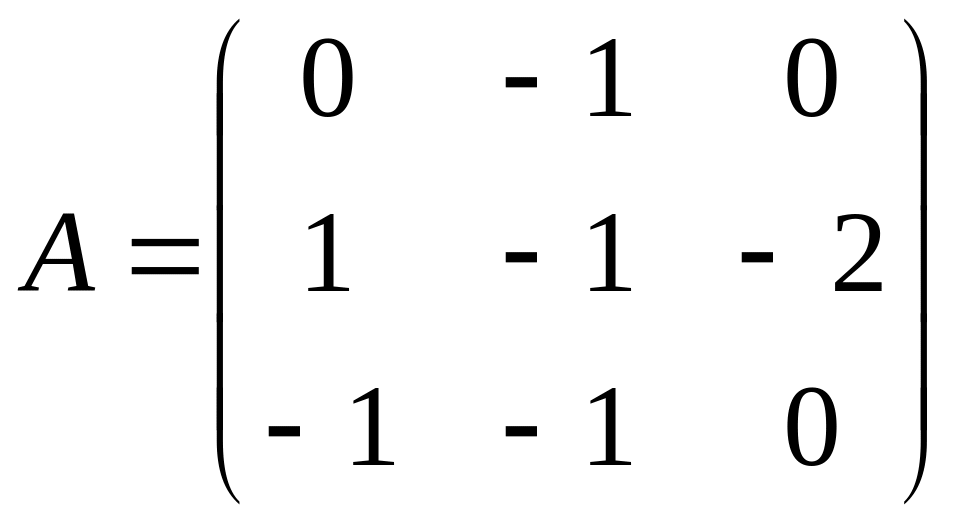 2.
2.
 3.
3.
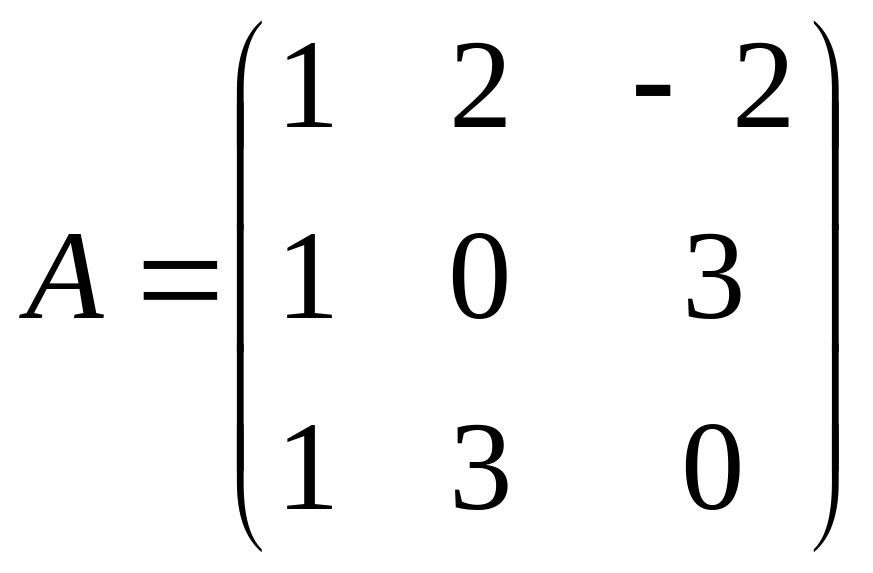
4.
 5.
5.
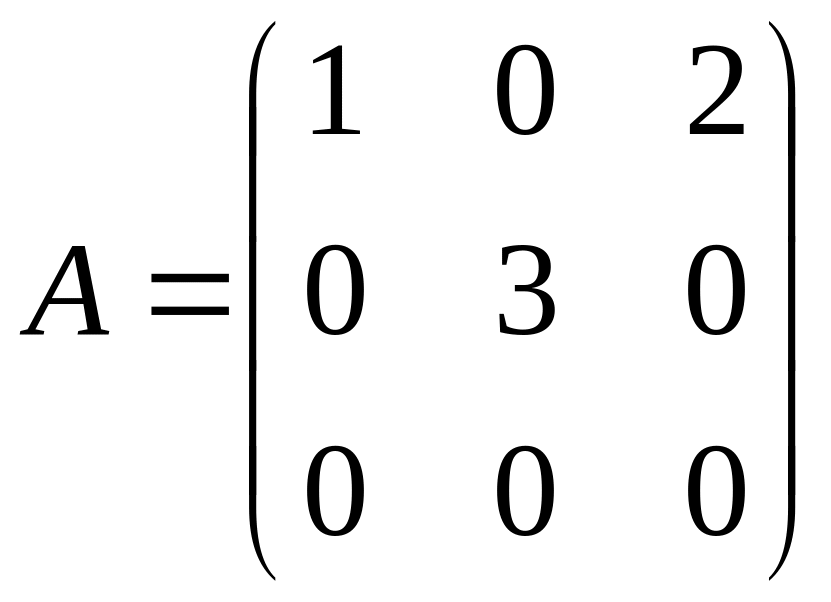 6.
6.

7.
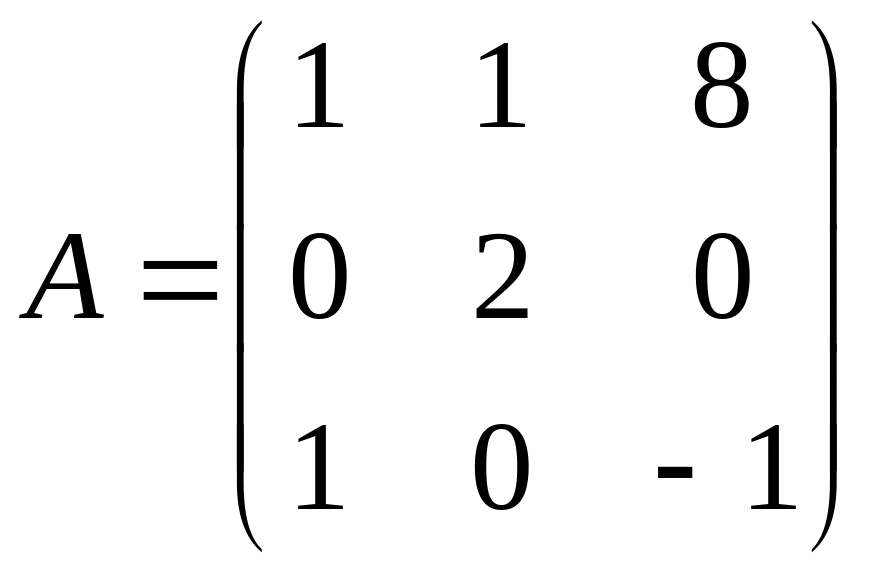 8.
8.
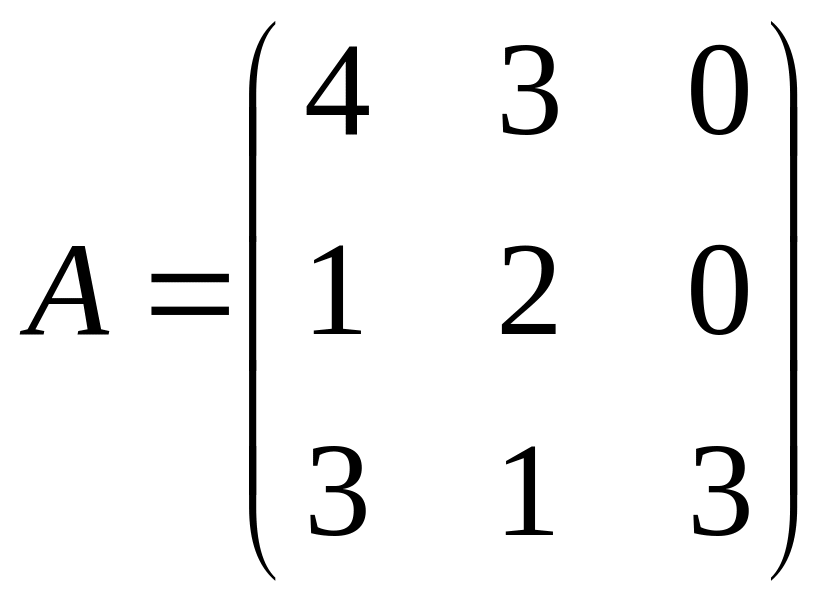 9.
9.

10.
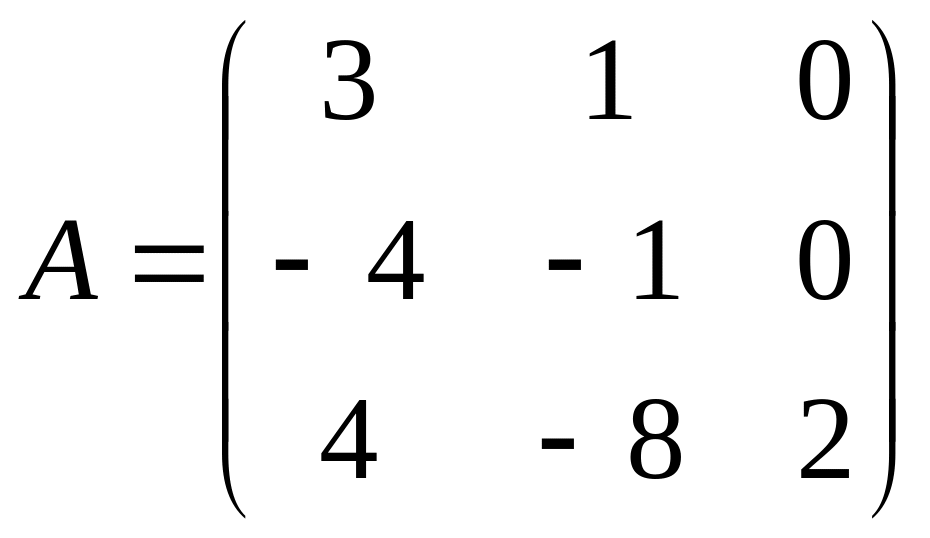 11.
11.
 12.
12.
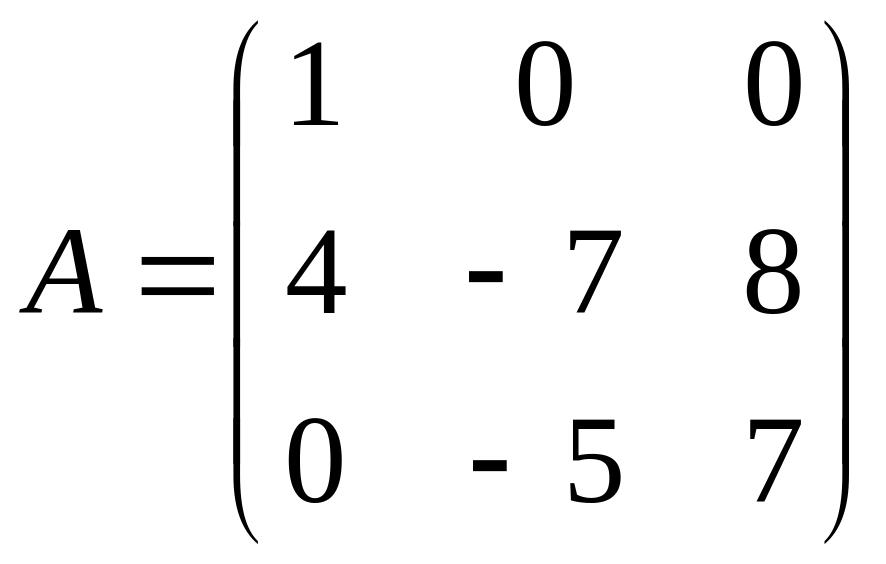
13.
 14.
14.
 15.
15.

16.
 17.
A=
17.
A= 18.
18.
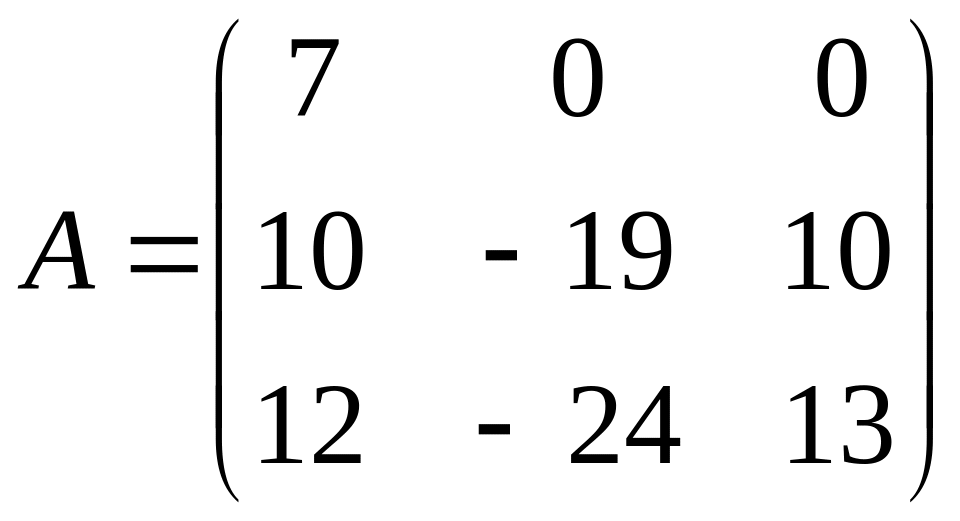
19.
 20.
20.
 21.
21.
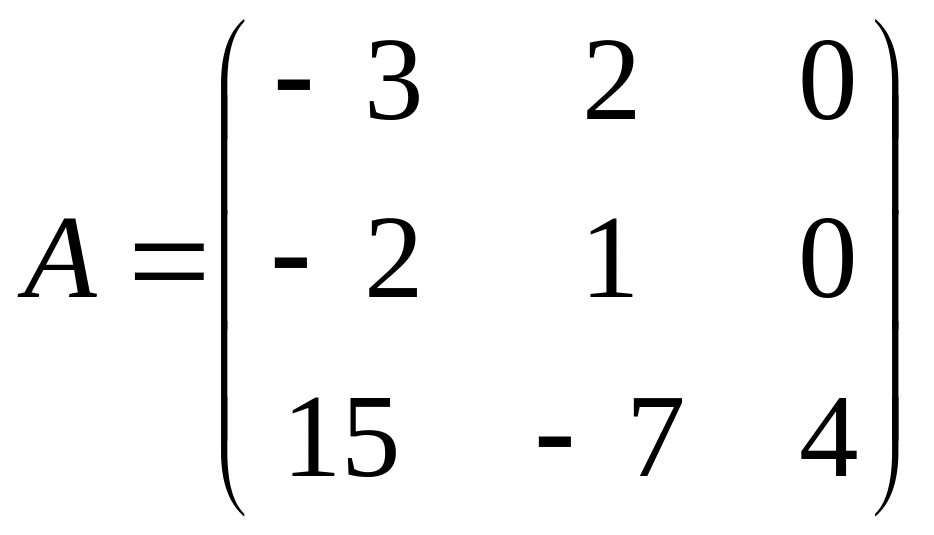
22.
 23.
23.
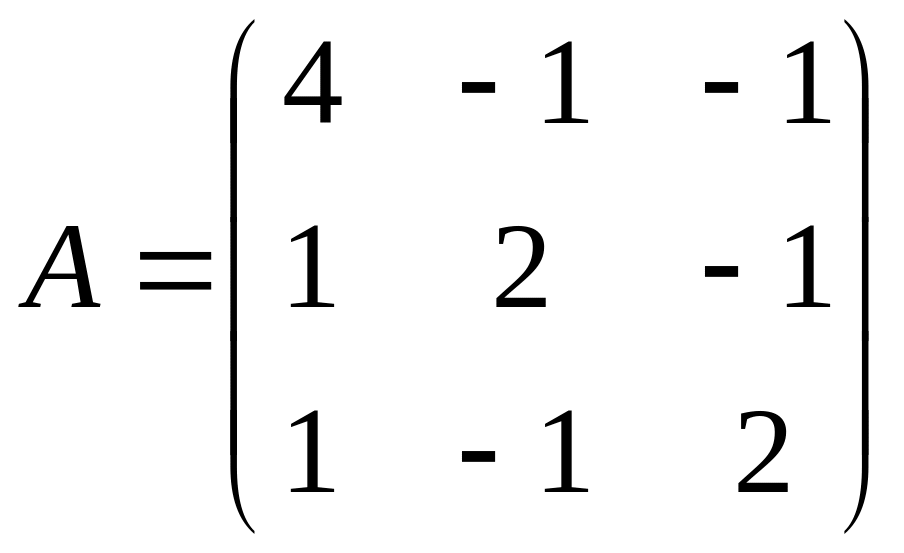 24.
24.

25.
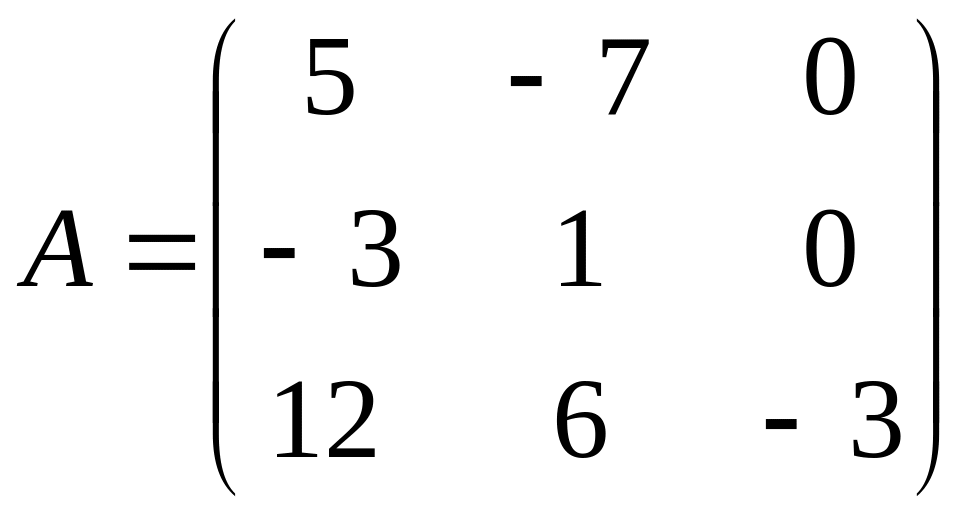 26.
26.
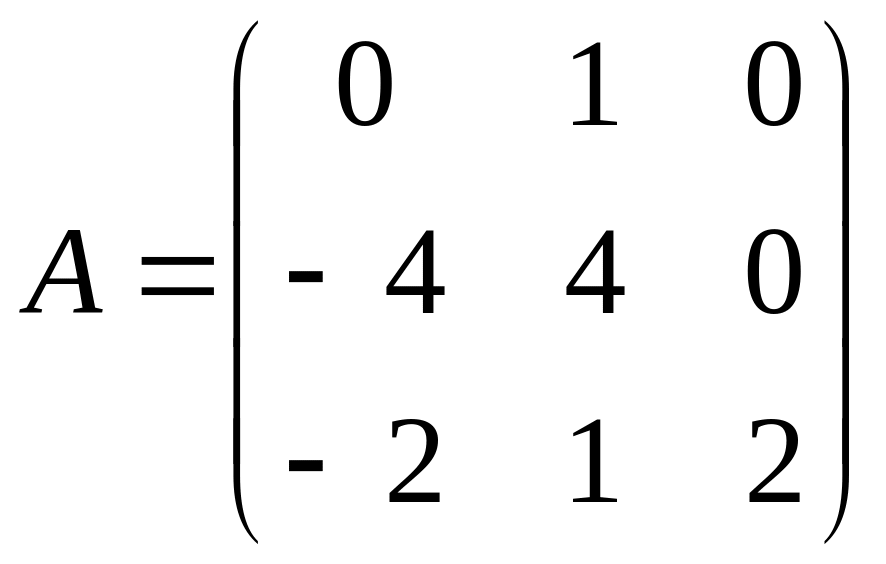 27.
27.
28.
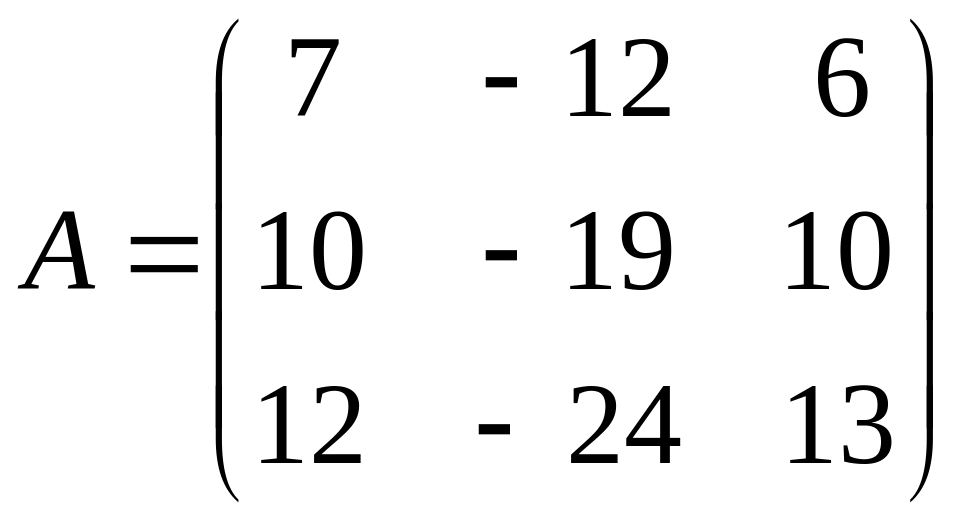 29.
29.
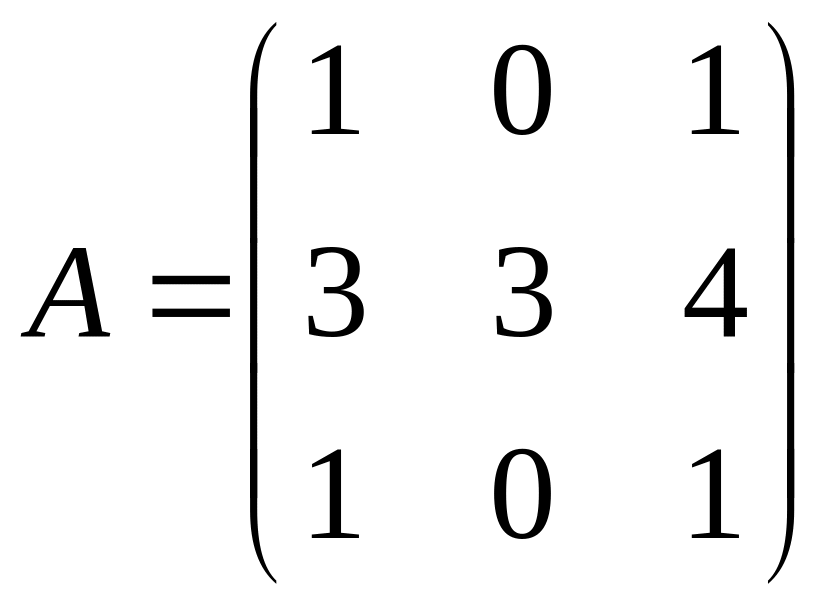 30.
30.

Задание 4.
Дано
комплексное число
![]() :
:
Записать число в алгебраической и тригонометрической формах.
Найти и изобразить на плоскости все корни уравнения Z3 + = 0.
1.
![]() 2.
2.
![]() 3.
3.
![]() 4.
4.
5.
![]() 6.
6.
![]() 7.
7.
![]() 8.
8.
![]()
9.
![]() 10.
10.
![]() 11.
11.
![]() 12.
12.
![]()
13.
![]() 14.
14.
![]() 15.
15.
![]() 16.
16.
![]()
17.
![]() 18.
18.
![]() 19.
19.
![]() 20.
20.
![]()
21.
![]() 22.
22.
![]() 23.
23.
![]() 24.
24.
![]()
25.
![]() 26.
26.
![]() 27.
27.
![]() 28.
28.
![]()
29.
![]() 30.
30.
![]()
