Тема 4. Произведение преобразований

Пусть даны линейные преобразования f и g соответственно с матрицами А и В в некотором базисе. Тогда произведение этих преобразований имеет матрицу ВА в том же базисе. Отметим, что в общем случае АВ  ВА.

Например, преобразование g с матрицей переводит точку М(х, у) в точку М(х, у) по формулам

. (2)

Преобразование А с матрицей переводит точку М(х, у) в точку М(Х₂, У₂) по формулам

, . (3)

Чтобы получить формулы результирующего преобразования точки М в точку М, надо подставить в (3) выражения (2). Получим

,

.

Стало быть, матрица произведения преобразований есть

.

Собственные числа и собственные векторы матрицы линейного преобразования (оператора)

Всякий ненулевой вектор называется собственным вектором линейного преобразования, если

А =λ , (4) где λ -некоторое число, называемое собственным значением (числом) линейного преобразования.

Если А - матрица линейного преобразования, Х - матрица-столбец из координат вектора , то равенство (1) можно записать в матричном виде

АХ = Х.

Перенося члены в одну сторону получим

AX- X=0 или (A- (5)

Уравнение для собственных значений называется характеристическим

уравнением .

Если матрица А имеет вид, то равенство (1.5.4) запи­сывается в виде системы линейных алгебраических уравнений

( a₁₁- λ)a₁+a₁₂a₂+...+a_1na_n=0

a₂₁a₁+(a₂₂- λ)a₂+...+a_2na_n=0

----------------------------------- (1.5.5)

a_n1a₁+a_n2a₂+...+(a_nn- λ)a_n=0

Система (1.5.5), однородная СЛАУ, имеет отличные от нуля (нетривиальные) решения только тогда, когда определитель равен нулю. Отсюда следует, что

det(A- λE)=0. (1.5.6) Уравнение (1.5.6) называется характеристическим уравнением матрицы данного линейного преобразования. Каждый действительный корень λ уравнения (1.5.6) является собственным числом. Соответствующие собственному числу координаты собственного вектора находятся из системы (1.5.5) методом, изложенном в теме 1.1 (см. пример 1.1.11).

П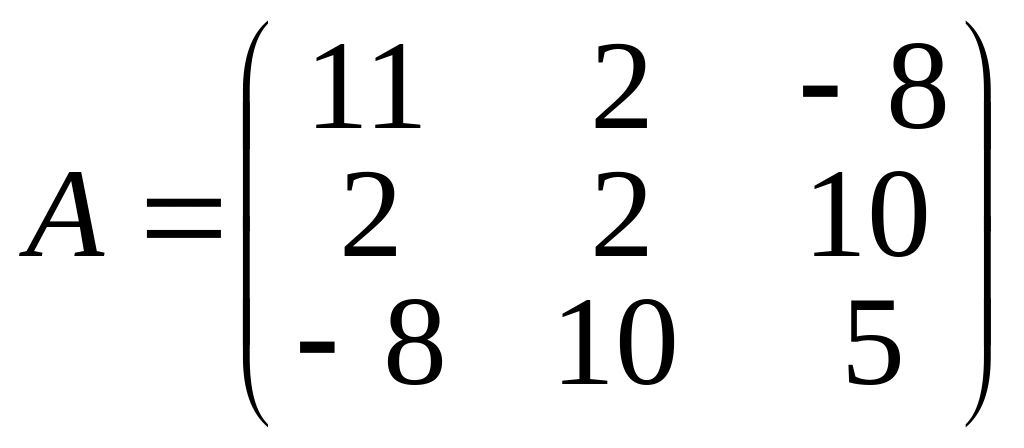 ример 1.5.4.Найти собственные числа и собственные векторы матрицы линейного преобразования

Система однородных линейных алгебраических уравнений (1.5.5) для нахождения собственных векторов имеет вид

(11-λ)x₁+2x₂-8x₃=0

2x₁+(2-λ)x₂+10x₃=0 (1.5.7)

-8x₁+10x₂+(5-λ)x₃=0

В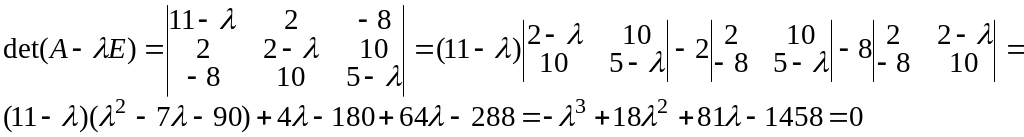 ычислим определитель (1.5.6) и решим соответствующее характеристическое уравнение

Характеристическое уравнение имеет вид

λ ³-18 λ²-81 λ+1458=0, а его решение λ₁=9, λ₂=18, λ₃=-9. Найденные зна­чения λ_i, і=1,3 подставим в (1.5.7)

Решение этой системы х₁= С(2,2,1)^Т, С єR, а соответствующий еди­ничный вектор х⁰₁ =(2/3, 2/3, 1/3) ^Т

При λ ₂=18: х⁰₂=(-2/3, 1/3, 2/3)^Т , при λ₃=-9: х⁰₃ =(1/3, -2/3, 2/3)