
- •Оглавление
- •Введение
- •Общие методические указания к решению задач и выполнению контрольных работ.
- •Глава 1. Кинематика поступательного и вращательного движения материальной точки
- •Основные формулы
- •1.1. Кинематика поступательного движения Примеры решения задача
- •1.2. Криволинейное движение Примеры решения задач
- •1.3. Вращательное движение Примеры решения задач
- •Глава 2. Динамика поступательного движения материальной точки и тела Основные формулы
- •Примеры решения задач
- •Глава 3. Работа и энергия при поступательном движении. Законы сохранения Основные формулы
- •Примеры решения задач
- •Глава 4. Динамика вращательного движения Основные формулы
- •Примеры решения задач
- •Глава 5. Работа и энергия при вращательном движении. Законы сохранения.
- •Примеры решения задач
- •Первый способ решения задачи:
- •Второй способ решения этой задачи:
- •Глава 6. Механические колебания. Волны в упругой среде. Аккустика. Основные формулы
- •Гармонические колебания. Сложение колебаний. Маятники. Примеры решения задач
- •6.2 Затухающие и вынужденные колебания. Примеры решения задач
- •6.3 Волны в упругой среде. Акустика. Примеры решения задач
- •Список рекомендуемой литературы.
- •Приложения
- •1. Формулы алгебры и тригонометрии
- •2. Таблица производных и интегралов
- •3. Таблица интегралов
Глава 2. Динамика поступательного движения материальной точки и тела Основные формулы
2.1. Импульс материальной точки (тела) и системы материальных точек (тел):


где n – число материальных точек (тел), входящих в рассматриваемую систему.
2.2. Основное уравнение динамики поступательного движения (второй закон Ньютона):
 или
или

где

масса,
масса,

ускорение,
ускорение,
 –
импульс материальной точки (тела).
–
импульс материальной точки (тела).
2.3. Третий закон Ньютона:

где

силы, с которыми взаимодействуют две
материальные точки (два тела).
силы, с которыми взаимодействуют две
материальные точки (два тела).
2.4. Силы в механике.
Сила упругости (закон Гука):

где

коэффициент упругости (в случае пружины
жесткость),
коэффициент упругости (в случае пружины
жесткость),

абсолютная деформация.
абсолютная деформация.
Сила трения скольжения:

где

коэффициент трения скольжения,
коэффициент трения скольжения,

сила нормальной реакции опоры.
сила нормальной реакции опоры.
Сила гравитационного притяжения

где

гравитационная постоянная,
гравитационная постоянная,

массы тел,
массы тел,

расстояние между телами (тела
рассматриваются как материальные
точки).
расстояние между телами (тела
рассматриваются как материальные
точки).
Примеры решения задач
Пример 1
Тело массой m = 2 кг движется прямолинейно по закону =A – Bt + Ct2 – Dt3 (C = 2 м/с2, D = 0,4 м/с3). Определите силу, действующую на тело в конце первой секунды движения.
Дано Решение
m = 2 кг , =A – Bt + Ct2–Dt3, C = 2 м/с2, D = 0,4 м/с3, t = 1 c |
Запишем второй закон Ньютона:
Ускорение равно первой производной от скорости по времени:
а скорость – это первая производная от пути по времени. Итак, |
F– ? |
 ;
;
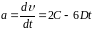 .
.
Тогда,
 (Н).
(Н).
Ответ: F = 3,2 H.
Пример 2
На
горизонтальной поверхности лежит тело
массой 10 кг. Какой путь пройдет оно за
время t
= 5 с, если к
нему приложить силу F
=100 Н, образующую
угол

![]() с горизонтом. Коэффициент трения между
телом и поверхностью
с горизонтом. Коэффициент трения между
телом и поверхностью

![]()
Дано Решение
|
|
S
|
На
тело действуют четыре силы: сила
тяжести
Спроектируем это уравнение на оси координат |
|
|
Выразим N из уравнения (2.3) и подставим в (2.4):
|
|
Силу
 ,
определяемую уравнением (2.5), подставим
в (2.2):
,
определяемую уравнением (2.5), подставим
в (2.2):
|
Откуда
 В
случае равноускоренного движения из
состояния покоя (
В
случае равноускоренного движения из
состояния покоя ( )
путь
,
пройденный телом за время
,равен:
)
путь
,
пройденный телом за время
,равен:
 (м).
(м).
Ответ:

Пример 3
Брусок
массы m
тянут за нить так, что он движется с
постоянной скоростью по горизонтальной
плоскости с коэффициентом трения μ.
Найти угол ,
при котором натяжение нити будет
наименьшим.
,
при котором натяжение нити будет
наименьшим.
Дано Решение
m, μ |
|
|








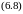





На брусок действуют силы: сила тяжести, сила реакции опоры, сила трения и сила натяжения нити.
Запишем второй закон Ньютона:
 (2.6)
(2.6)
Так
так брусок движется с постоянной
скоростью, следовательно, ускорение
 .
Выберем оси
и
,
как показано на рисунке. В проекции на
эти оси векторное уравнение (2.6) имеет
вид:
.
Выберем оси
и
,
как показано на рисунке. В проекции на
эти оси векторное уравнение (2.6) имеет
вид:
 (2.7)
(2.7)
 . (2.8)
. (2.8)
Тело
движется по поверхности, при этом сила
трения скольжения
 .
Значение силы
.
Значение силы
 определяем из уравнения (2.8):
определяем из уравнения (2.8):

Тогда,
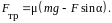
Подставляя выражение для силы трения в уравнение (2.7), получим:

Так
как по условию задачи натяжение нити
должно быть наименьшим, берем производную
от силы
 по углу
по углу
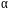 и приравниваем полученный результат к
нулю:
и приравниваем полученный результат к
нулю:
 .
.
Отсюда следует, что

Поделим
это уравнение на
 и получим:
и получим:
 и
и
 .
.
Ответ: натяжение нити будет наименьшим при угле .
Пример 4
На
горизонтальной платформе шахтной клети
стоит человек массой m
= 60 кг.
Определите силу давления человека на
платформу: 1) при ее подъеме с ускорением
а1
= 3 м/с2;
2) при равномерном подъеме и спуске; 3)
при спуске с ускорением

Дано Решение
m = 60 кг,
a1 = 3 м/с2 , a2 = 0, a3 = 9,8 м/с |
|
|
Н

 и сила реакции опоры
и сила реакции опоры
 .
Запишем второй закон Ньютона:
.
Запишем второй закон Ньютона:
 . (2.9)
. (2.9)
По третьему закону Ньютона сила давления человека на платформу равна силе реакции опоры:
 ;
;
 .
.
1.
Запишем уравнение (2.9) в проекции на ось
 при подъеме клети:
при подъеме клети:
 .
.
Отсюда 
Таким
образом,

 .
.
2.
При равномерном движении шахтной клети
 и, следовательно, сила давления человека
на платформу равна силе тяжести:
и, следовательно, сила давления человека
на платформу равна силе тяжести:
 ,
,
 .
.
3. При спуске платформы с ускорением, направленным вниз, уравнение движения платформы имеет вид:
 .
.
Откуда сила давления человека на платформу
 .
.
Учитывая,
что
 имеем
имеем
 .
Следовательно, человек не давит на
платформу.
.
Следовательно, человек не давит на
платформу.
Ответ:
 ,
,
 ,
.
,
.
Пример 5
К
динамометру, подвешенному в кабине
лифта, прикреплен груз массой
 кг.
Лифт движется вверх. Определить ускорение
кг.
Лифт движется вверх. Определить ускорение
 лифта, считая его одинаковым, если
известно, что во время разгона показания
динамометра больше, чем при торможении
на
лифта, считая его одинаковым, если
известно, что во время разгона показания
динамометра больше, чем при торможении
на
 Н.
Н.
Дано Решение
|
При разгоне При торможении |
–? |
На
груз действуют две силы: сила тяжести
 ,
сила упругости со стороны пружины
,
сила упругости со стороны пружины
 – при разгоне и
– при разгоне и
 – при торможении.
– при торможении.
По
третьему закону Ньютона эти силы равны
силам
 и
и
 ,
с которыми груз действует на пружину
динамометра при разгоне и торможении
соответственно, то есть это показания
динамометра.
,
с которыми груз действует на пружину
динамометра при разгоне и торможении
соответственно, то есть это показания
динамометра.
 ;
;
 .
.
Запишем основной закон динамики:
 – при разгоне
– при разгоне
 – при торможении.
– при торможении.
Спроектируем
данные уравнения на ось
 , учитывая при этом направление ускорений
, учитывая при этом направление ускорений
 и
и



По условию задачи
 и
и
 .
.
Вычтем из верхнего уравнения нижнее и получим:

Откуда 
Ответ:

Пример 6
Определить
усилие, необходимое для равномерного
перемещения вдоль наклонной плоскости
груза массой m
= 450 кг. Угол
при основании наклонной плоскости равен
 ,
коэффициент трения скольжения 0,2.
,
коэффициент трения скольжения 0,2.
Дано Решение
,
|
|
|
На
тело, движущееся вдоль наклонной
плоскости, действуют: сила тяжести
 ,
реакция опоры
,
реакция опоры
 ,
сила трения скольжения
,
сила трения скольжения
 ,
сила тяги
,
сила тяги
 .
Основное уравнение динамики примет
следующий вид:
.
Основное уравнение динамики примет
следующий вид:
 .
.
Для
получения скалярных уравнений движения
необходимо выбрать прямоугольную
систему координат
 и спроектировать уравнение на каждую
из осей:
и спроектировать уравнение на каждую
из осей:





Используя
условие задачи, связанное с равенством
нулю ускорения
 ,
получаем:
,
получаем:


Решая эту систему, находим выражение для искомой величины:
|
|
Подставим числовые значения:
 (Н).
(Н).
Ответ:
 Н.
Н.
Пример 7
Определить период вращения искусственного спутника Земли (ИСЗ) считая, что он движется по круговой орбите на высоте 300 км над поверхностью земли.
Дано Решение
|
|
Т–? |
Тело
(ИСЗ), выведенное на околоземную орбиту,
движется по окружности под действием
силы всемирного тяготения
 , которая направлена к центру земли и
определяется соотношением:
, которая направлена к центру земли и
определяется соотношением:
 ,
,
где
 –
гравитационная постоянная;
–
гравитационная постоянная;
 –
масса Земли;
–
высота орбиты;
–
масса Земли;
–
высота орбиты;
 –
радиус Земли.
–
радиус Земли.
Основное
уравнение динамики может быть записано
в следующей форме:  .
.
Спроектировав данное уравнение на ось, проведенную к центру Земли, получим:
 .
.
Как
известно, величина центростремительного
ускорения
может быть связана с угловой скоростью
 ,
а так же с периодом обращения Т
,
а так же с периодом обращения Т
 следующими соотношениями:
следующими соотношениями:
 или
или

Итак,

Отсюда получаем искомое выражение для периода обращения Т:

Проведём расчет:

Ответ:
период обращения ИСЗ на высоте
![]() км
составляет 91 мин.
км
составляет 91 мин.
Пример 8
Два
груза массами
![]() кг
и
кг
и
![]() кг
каждый связаны нитью и движутся по
горизонтальной поверхности под действием
силы 20 Н, направленной под углом
кг
каждый связаны нитью и движутся по
горизонтальной поверхности под действием
силы 20 Н, направленной под углом
![]() к горизонту. Определить ускорения
системы
и силу натяжения нити Т,
если коэффициент трения
к горизонту. Определить ускорения
системы
и силу натяжения нити Т,
если коэффициент трения
![]() .
.
Дано Решение
,
|
|
1) –? 2) Т –? |
Мы
имеем систему, состоящую из двух тел.
На первое тело действует пять сил: сила
тяжести
 ,
сила тяги
,
сила тяги
![]() сила
реакции опоры
сила
реакции опоры![]() ,
сила натяжения нити
,
сила натяжения нити
![]() и сила трения
и сила трения
![]() .
На второе тело действует четыре силы:
сила тяжести
.
На второе тело действует четыре силы:
сила тяжести
![]() ,
сила реакции опоры
,
сила реакции опоры![]() ,
сила натяжения нити
,
сила натяжения нити
![]() и сила трения
и сила трения
![]() .
.
Запишем
уравнения динамики для каждого тела
системы. При этом учтем, что тела движутся
с одинаковым ускорением
![]() .
Это следует из условия нерастяжимости
нити. Из условия невесомости нити
следует, что силы натяжения
и
равны:
.
Это следует из условия нерастяжимости
нити. Из условия невесомости нити
следует, что силы натяжения
и
равны:
![]()
Итак,
![]()
![]()
Спроектируем эти уравнения на оси ox и oy .
Для первого тела:
![]()
![]()
![]()
Для второго тела:
![]()
![]()
![]()
Преобразования для первой системы дают:
![]()
![]()
![]() (2.10)
(2.10)
Преобразования для второй системы:
![]()
![]()
![]() (2.11)
(2.11)
Объединим уравнения (2.10) и (2.11) и сложим
![]() (2.12)
(2.12)
Итак,
![]()
Из
этого уравнения выражаем ускорение
![]()

Приведём вычисление:

Найдем силу натяжения из уравнения (2.11):
![]()
Подставим числовые значения
![]()
Ответ:
![]() м/с2;
м/с2;
![]() Н.
Н.
Пример 9
Простейшая машина Атвуда, применяемая для изучения законов равноускоренного движения, представляет собой два груза с неравными массами m1 и m2 (например m1>m2), которые подвешены на легкой нити, перекинутой через неподвижный блок. Считая нить и блок невесомыми и пренебрегая трением в оси блока, определите:
1)
ускорение грузов; 2) силу натяжения нити
T;
3) силу
 ,
действующую на ось блока.
,
действующую на ось блока.
Дано Решение
m1, m2, m1>m2 |
|
1) – ? 2) T – ? 3) – ? |
Так
как
![]() >
>![]() ,
то груз массой
будет опускаться вниз с ускорением
,
то груз массой
будет опускаться вниз с ускорением
![]() ,
а груз массой
будет подниматься вверх с ускорением
,
а груз массой
будет подниматься вверх с ускорением
![]() .
.
По второму закону Ньютона:
![]() , (2.12)
, (2.12)
![]() , (2.13)
, (2.13)
где
![]() и
и
![]() – силы тяжести и силы натяжения нити
для грузов
– силы тяжести и силы натяжения нити
для грузов
![]() и
и
![]() .
Из условия нерастяжимости и невесомости
нити следует, что
.
Из условия нерастяжимости и невесомости
нити следует, что
![]() ;
;
![]() ;
;
![]() .
.
Так как блок невесомый, то силы натяжения нити по обе стороны блока равны:
![]() . (2.14)
. (2.14)
и
соответственно ![]()
В
проекциях на оси
![]() и
и
![]() уравнения (2.12) и (2.13) с учетом (2.14) принимают
вид:
уравнения (2.12) и (2.13) с учетом (2.14) принимают
вид:

Сложив эти два уравнения, получим:
![]()
После преобразования находим:
 ;
;
 .
.
Сила давления на ось блока

Ответ:



Пример 10
Грузы одинаковой массой (m1= m2 = 0,5 кг) соединены нитью и перекинуты через невесомый блок, укрепленный на конце стола. Коэффициент трения груза m2 о стол μ = 0,15. Пренебрегая трением в блоке, определите: 1) ускорение, с которым движутся грузы; 2) силу натяжения нити.
Дано Решение
m1= m2= 0,5кг,
|
|
1) а – ? 2) T – ? |
Так как нить невесомая и нерастяжимая, то
![]() ;
;
![]() ,
,
![]() .
.
Поскольку блок невесомый, то силы натяжения нитей по обе стороны блока равны (см. задачу 9):
![]()
Запишем второй закон Ньютона для каждого тела:

Спроектировав эти уравнения на выбранные оси, получим:
![]() ;
;
![]() ;
;
![]() .
.
Из
последнего уравнения определяем
![]() :
:
![]()
При скольжении:
![]() .
.
С учетом приведенных выше соотношений уравнения примут вид:

Сложим эти уравнения и получим:
![]() .
.
Тогда,
 ;
;
![]()
Подставим
числовые значения в выражения для
и
![]() :
:
 ;
;
![]() .
.
Ответ:
1)
![]() 4,17м/с2;
2)
4,17м/с2;
2)
![]() 2,82
Н.
2,82
Н.
Пример 11
На какой угол отклонится канат “гигантских шагов”, если мальчик вращается частотой 15 об/мин, а длинна каната составляет 6 м.
Дано Решение
|
|
|
На
вращающееся тело действуют силы тяжести
![]() ,
натяжения каната
,
натяжения каната
![]() .
Основное уравнение динамики должно
быть записано в виде
.
Основное уравнение динамики должно
быть записано в виде
![]() (2.15)
(2.15)
Для
получения скалярных уравнений применяем
стандартный приём: проектируем уравнение
(2.15) на взаимно перпендикулярные оси
![]() и
и
![]() .
Тогда уравнение (2.15) “распадается” на
два скалярных уравнения:
.
Тогда уравнение (2.15) “распадается” на
два скалярных уравнения:
 (2.16)
(2.16)
Исключив
из системы (2.16) величину
и подставив выражение для центростремительного
ускорения в виде
![]() в (2.16), получим
в (2.16), получим
 .
.
В дальнейшем, используя соотношения между величинами
 :
:
![]() ,
,
 :
:
![]() ,
,
Получаем  .
.
Откуда  .
.
Проведём расчёт:
 .
.
Ответ:
![]() .
.
Пример 12
Две пружины одной и той же длины, жёсткость которых k1 и k2 соответственно, соединены или последовательно, или параллельно. Каково отношение жесткости системы из двух пружин, соединёных последовательно, к жёсткости системы этих пружин при их параллельном соединении?
Дано Решение
|
|
|
Последовательно Параллельно
В случае последовательного соединения пружин силы упругости, возникающие в них, одинаковы и равны по модулю внешней силе F :
![]() (2.17)
(2.17)
где Fупр.- сила упругости, возникающая в нижней пружине жесткостью k2 под действием внешней силы F; Fупр.- сила упругости, действующая со стороны верхней пружины на нижнюю.
Суммарное удлинение (абсолютная деформация) x системы двух последовательно соединённых пружин под действием внешней силы равно алгебраической сумме удлинений (абсолютных деформаций) x1 и x2 этих пружин:
![]() (2.18)
(2.18)
По закону Гука записываем:
 (2.19)
(2.19)
 (2.20)
(2.20)
 (2.21)
(2.21)
здесь kпосл.- жесткость системы двух пружин, соединённых последовательно. Подставляя формулы (2.19), (2.20), (2.21) в равенство (2.18), с учётом (2.17) получим
 (2.22)
(2.22)
В случае параллельного соединения пружин удлинение (абсолютная деформация) x системы равно удлинению (абсолютной деформации) x1 и x2 каждой из этих пружин:
![]() (2.23)
(2.23)
а внешняя сила F равна по модулю алгебраической сумме сил упругости Fупр. 1 и Fупр. 2, возникающих в пружинах при их деформации:
![]() (2.24)
(2.24)
По закону Гука имеем
![]() (2.25)
(2.25)
где kпар. – жесткость системы двух пружин, соединённых параллельно.
Подставляя формулы (2.25) в равенство (2.24), с учётом (2.23) будем иметь
![]() (2.26)
(2.26)
Из (2.22) и (2.26) находим

Ответ:
Пример 13
Тело движется вниз равноускоренно по наклонной плоскости, и
зависимость
пройденного телом пути
![]() от времени
задается
уравнение
от времени
задается
уравнение
![]() Найти коэффициент трения
тела о плоскость, если угол наклона
плоскости к горизонту равен
Найти коэффициент трения
тела о плоскость, если угол наклона
плоскости к горизонту равен
![]() .
.
Дано Решение
|
|
–? |
Коэффициент
трения
определяет
силу трения при движении тел. Для
нахождения
рассмотрим
под действием каких сил находится тело.
В данном случае на тело действуют три
силы: сила тяжести
![]() ,
сила реакции опоры
и сила трения
,
сила реакции опоры
и сила трения
 .
.
Выберем
систему координат так, чтобы ось
![]() была направлена вдоль наклонной
плоскости. Тогда, согласно второму
закону Ньютона, запишем проекции сил
на оси
была направлена вдоль наклонной
плоскости. Тогда, согласно второму
закону Ньютона, запишем проекции сил
на оси
![]() и
и
![]() :
:
![]()
![]()
![]()

Из второго уравнения выражаем N и подставляем в третье уравнение:
![]()
Далее силу трения подставляем в первое уравнение
![]()
Отсюда выражаем коэффициент трения :
 .
.
Определим величину ускорения :
 а
а

Таким образом,

Подставив в формулу для численные значения входящих в нее величин, получим коэффициент трения:
 .
.
Ответ:
![]() .
.
Пример 14
Под каким наименьшим углом к горизонту может стоять прислонённая к идеально гладкой стене лестница, если известно, что коэффициент трения лестницы равен ?
Дано Решение
|
|
|
Рассмотрим
силы действующие на лестницу. Со стороны
Земли
![]() сила тяжести
сила тяжести
![]() .
Со стороны вертикальной стенки действует
только сила нормальной реакции
.
Со стороны вертикальной стенки действует
только сила нормальной реакции
![]() .
Со стороны пола действует сила нормальной
реакции
.
Со стороны пола действует сила нормальной
реакции
![]() и сила трения
и сила трения
![]() направленная в сторону, противоположную
тому движению нижнего конца лестницы,
которое было бы в отсутствии трения. В
отсутствии трения лестница должна
скользить вправо по полу, следовательно,
направлена влево.
направленная в сторону, противоположную
тому движению нижнего конца лестницы,
которое было бы в отсутствии трения. В
отсутствии трения лестница должна
скользить вправо по полу, следовательно,
направлена влево.
Для равновесия необходимы: равенство нулю геометрической суммы всех внешних сил и равенство нулю алгебраической суммы моментов внешних относительно любой неподвижной оси.
Первое условие даёт:
![]()
или в проекциях на оси x и y:
 (2.27)
(2.27)
 (2.28)
(2.28)
Уравнение моментов удобно написать относительно оси, проходящей через току О. Пусть длина лестницы l , тогда:
 (2.29)
(2.29)
Так как возникшая сила трения есть сила трения покоя, то:
 (2.30)
(2.30)
Из (2.28) и (2.29) находим:
![]()
откуда с учётом (2.30) имеем:

то
есть  . (2.31)
. (2.31)
Таким образом, лестница будет в равновесии, если она наклонена к полу под углом, который удовлетворяет условию (2.31). Наименьший угол, при котором лестница ещё будет сохранять равновесие, удовлетворяет условию:

Ответ:

Задачи
41. Поезд
массой
![]() т,
двигаясь равнозамедленно, в течение
времени
мин
уменьшил свою скорость от
т,
двигаясь равнозамедленно, в течение
времени
мин
уменьшил свою скорость от
 км/ч
до
км/ч
до
 км/ч.
Найти силу торможения
км/ч.
Найти силу торможения
![]() .
.
42. На
автомобиль массой
![]() т
во время движения действует сила трения
т
во время движения действует сила трения
 ,
равная 0,1 действующей на него силы
тяжести
.
Найти силу
тяги
,
развиваемую
мотором автомобиля, если автомобиль
движется с ускорением
,
равная 0,1 действующей на него силы
тяжести
.
Найти силу
тяги
,
развиваемую
мотором автомобиля, если автомобиль
движется с ускорением
![]() м/с2
в гору с уклоном 1 м на каждые 25 м пути.
м/с2
в гору с уклоном 1 м на каждые 25 м пути.
43. Тело
скользит по наклонной плоскости,
образующей с горизонтом угол
 .
Пройдя путь
.
Пройдя путь
 см,
тело приобретает скорость
см,
тело приобретает скорость
![]() м/с.
Найти коэффициент трения
м/с.
Найти коэффициент трения
 тела о плоскость.
тела о плоскость.
44. Трамвай,
трогаясь с места, движется с ускорением
![]() м/с2.
Через время
м/с2.
Через время
![]() с
после начала движения мотор выключается,
и трамвай движется до остановки
равнозамедленно. Коэффициент трения
на всем пути
с
после начала движения мотор выключается,
и трамвай движется до остановки
равнозамедленно. Коэффициент трения
на всем пути
 .
Найти наибольшую скорость
и время
движения
трамвая. Каково его ускорение
при равнозамедленном движении? Какое
расстояние
пройдет трамвай за время движения?
.
Найти наибольшую скорость
и время
движения
трамвая. Каково его ускорение
при равнозамедленном движении? Какое
расстояние
пройдет трамвай за время движения?
45. Под
действием силы
![]() Н
тело движется прямолинейно так, что
зависимость пройденного телом пути
от времени
дается уравнением
,
где
м/с2.
Найти массу
Н
тело движется прямолинейно так, что
зависимость пройденного телом пути
от времени
дается уравнением
,
где
м/с2.
Найти массу
![]() тела.
тела.
46. Вагон
массой
![]() т
движется равнозамедленно, имея начальную
скорость
т
движется равнозамедленно, имея начальную
скорость
 км/ч
и ускорение
км/ч
и ускорение
![]() м/с2.
Какая сила торможения
действует
на вагон? Через какое время
вагон остановится? Какое расстояние
м/с2.
Какая сила торможения
действует
на вагон? Через какое время
вагон остановится? Какое расстояние
![]() вагон
пройдет до остановки?
вагон
пройдет до остановки?
47. Тело
лежит на наклонной плоскости, образующей
с горизонтом угол
 .
При каком предельном коэффициенте
трения
.
При каком предельном коэффициенте
трения
![]() тело начнет скользить по наклонной
плоскости? С каким ускорением
будет скользить тело по плоскости, если
коэффициент трения
тело начнет скользить по наклонной
плоскости? С каким ускорением
будет скользить тело по плоскости, если
коэффициент трения
![]() ? Какое
время
потребуется
для прохождения при этих условиях пути
? Какое
время
потребуется
для прохождения при этих условиях пути
 м?
Какую скорость
тело будет иметь в конце пути?
м?
Какую скорость
тело будет иметь в конце пути?
48. На
автомобиль массой
т
во время движения действует сила трения
,
равная 0,1 действующей на него силы
тяжести
.
Какова должна быть сила тяги
,
развиваемая
мотором автомобиля, чтобы автомобиль
двигался: а) равнозамедленно; б) с
ускорением
![]() м/с2?
м/с2?
49. Вагон
массой
т
движется равнозамедленно, имея начальную
скорость
![]() км/ч
и ускорение
м/с2.
Какая сила торможения действует на
вагон? Через какое время
вагон
остановится? Какое расстояние
вагон пройдет до остановки?
км/ч
и ускорение
м/с2.
Какая сила торможения действует на
вагон? Через какое время
вагон
остановится? Какое расстояние
вагон пройдет до остановки?
50. Тело
скользит по наклонной плоскости,
образующей с горизонтом угол
 .
Зависимость пройденного телом пути
от времени
дается
уравнением
.
Зависимость пройденного телом пути
от времени
дается
уравнением
 ,
где
,
где
![]() м/с2.
Найти коэффициент трения
тела о плоскость.
м/с2.
Найти коэффициент трения
тела о плоскость.
51. Автомобиль
движется вверх по наклонной плоскости
с начальной скоростью
 м/с.
Определить путь
,
пройденный автомобилем до остановки и
время
его движения, если коэффициент трения
м/с.
Определить путь
,
пройденный автомобилем до остановки и
время
его движения, если коэффициент трения
 ,
а угол наклона
,
а угол наклона
 .
.
52. На
горизонтальной поверхности лежит тело
массой
![]() кг.
Какой путь пройдет тело за время
кг.
Какой путь пройдет тело за время
![]() с,
если к нему приложить силу
с,
если к нему приложить силу
![]() H,
образующую угол
H,
образующую угол
 с
горизонтом. Коэффициент трения между
телом и поверхностью
с
горизонтом. Коэффициент трения между
телом и поверхностью
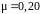 .
.
53. К
динамометру, подвешенному в кабине
лифта, прикреплен груз массой
![]() кг.
Лифт движется вверх. Определить ускорение
лифта, считая его одинаковым по модулю
при разгоне и торможении, если известно,
что во время разгона показание динамометра
больше, чем при торможении на
кг.
Лифт движется вверх. Определить ускорение
лифта, считая его одинаковым по модулю
при разгоне и торможении, если известно,
что во время разгона показание динамометра
больше, чем при торможении на
![]() H.
H.
54. Два
груза
кг
каждый связаны нитью и движутся по
горизонтальной поверхности под действием
силы
H,
направленной под углом
 к горизонту. Определить ускорение
системы и силы натяжения нити T1
и T2,
если коэффициент трения
к горизонту. Определить ускорение
системы и силы натяжения нити T1
и T2,
если коэффициент трения
 .
.
55. Строительный
блок массой
![]() т
лежит на дне кабины подъемника. Определить
силу
давления на пол при подъеме вертикально
вверх согласно уравнению
т
лежит на дне кабины подъемника. Определить
силу
давления на пол при подъеме вертикально
вверх согласно уравнению ,
где
,
где
![]() м/с,
м/с,
![]() м/с.
м/с.
56. На
наклонную плоскость, составляющую угол
 с горизонтом, положили тело, которое
начало скользит вниз без начальной
скорости. Найти его скорость через
с горизонтом, положили тело, которое
начало скользит вниз без начальной
скорости. Найти его скорость через
![]() с
после начала движения, если коэффициент
трения тела о плоскость равен
.
с
после начала движения, если коэффициент
трения тела о плоскость равен
.
57. К нити подвешен груз массой г. Определите натяжение нити, если нить с грузом: 1) поднимать с ускорением м/с2; 2) опускать с ускорением м/с2.
58. Тело
массой
![]() кг
падает вертикально с ускорением
кг
падает вертикально с ускорением
![]() м/с2.
Определите силу сопротивления при
движении этого тела.
м/с2.
Определите силу сопротивления при
движении этого тела.
59. С
вершины клина, длина которого
![]() м
и высота
м,
начинает скользить небольшое тело.
Коэффициент трения между телом и клином
м
и высота
м,
начинает скользить небольшое тело.
Коэффициент трения между телом и клином
 .
Определите: 1) ускорение, с которым
движется тело; 2) время прохождения тела
вдоль клина; 3) скорость тела у основания
клина.
.
Определите: 1) ускорение, с которым
движется тело; 2) время прохождения тела
вдоль клина; 3) скорость тела у основания
клина.
60. По наклонной плоскости с углом а наклона к горизонту, равным 30°, скользит тело. Определите скорость тела в конце второй секунды от начала скольжения, если коэффициент трения .

 .
. ,
, кг,
кг, Н,
Н, ,
, с,
с,

 ?
? ,
сила реакции опоры
,
сила реакции опоры
 ,
сила тяги
,
сила тяги
 и сила трения
и сила трения
 .Запишем
второй закон Ньютона:
.Запишем
второй закон Ньютона:
 (2.1)
(2.1) (2.2)
(2.2) (2.3)
(2.3) (2.4)
(2.4) . (2.5)
. (2.5)

 =
const,
=
const,


 Н
Н
 кг,
кг,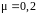 ,
,

 ?
?
 км,
км, км,
км, кг
кг









