
- •Оглавление
- •Введение
- •Общие методические указания к решению задач и выполнению контрольных работ.
- •Глава 1. Кинематика поступательного и вращательного движения материальной точки
- •Основные формулы
- •1.1. Кинематика поступательного движения Примеры решения задача
- •1.2. Криволинейное движение Примеры решения задач
- •1.3. Вращательное движение Примеры решения задач
- •Глава 2. Динамика поступательного движения материальной точки и тела Основные формулы
- •Примеры решения задач
- •Глава 3. Работа и энергия при поступательном движении. Законы сохранения Основные формулы
- •Примеры решения задач
- •Глава 4. Динамика вращательного движения Основные формулы
- •Примеры решения задач
- •Глава 5. Работа и энергия при вращательном движении. Законы сохранения.
- •Примеры решения задач
- •Первый способ решения задачи:
- •Второй способ решения этой задачи:
- •Глава 6. Механические колебания. Волны в упругой среде. Аккустика. Основные формулы
- •Гармонические колебания. Сложение колебаний. Маятники. Примеры решения задач
- •6.2 Затухающие и вынужденные колебания. Примеры решения задач
- •6.3 Волны в упругой среде. Акустика. Примеры решения задач
- •Список рекомендуемой литературы.
- •Приложения
- •1. Формулы алгебры и тригонометрии
- •2. Таблица производных и интегралов
- •3. Таблица интегралов
Гармонические колебания. Сложение колебаний. Маятники. Примеры решения задач
Пример 1.
Запишите уравнение гармонического колебательного движения точки, совершающей колебания амплитудой А=8 см, если за t=1 мин совершается N=120 колебаний и начальная фаза колебаний равна 45°.
Дано Решение
А=8 см=8·102м, t = 1 мин=60 с, N= 120,
|
Уравнение гармонического колебания имеет вид
|
x(t)- ? |

Итак,  ,
,
тогда движение будет иметь вид:

Ответ
:
![]() .
.
Пример 2.
Точка
совершает гармонические колебания по
закону
![]() м.
Определите: 1) период Т
колебаний; 2) максимальную скорость
м.
Определите: 1) период Т
колебаний; 2) максимальную скорость
 точки; 3) максимальное ускорение
точки; 3) максимальное ускорение
 точки.
точки.
Дано Решение
|
Уравнение гармонических колебаний имеет вид
В
нашем случае А=3
м,
Скорость
колеблющейся точки
производная от смещения по времени |
1)Т ? 2) 3) |

Максимальная
скорость достигается при значении
![]() и тогда
и тогда
 .
.
Ускорение точки– это первая производная от скорости по времени, то есть
Считаем
при максимальном ускорении
![]() следовательно
следовательно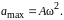 Период колебаний находим по формуле:
Период колебаний находим по формуле:
![]()
Подставляем
числовые значения и определяем
 и
и
![]() :
:
 м/с;
м/с;
 .
.
Ответ:
1) Т=
4 с; 2)
 м/с;
3)
м/с;
3)

Пример 3.
Наибольшее
смещение точки, совершающей гармонические
колебания, равно
 наибольшая
скорость –
наибольшая
скорость –
 Найдите
циклическую частоту колебаний
Найдите
циклическую частоту колебаний
 ,
максимальное ускорение точки
,
максимальное ускорение точки
 и период колебаний
.
и период колебаний
.
Дано Решение
|
Запишем уравнение гармонических колебаний:
где
|
|
Взяв первую производную смещения (6.1) по времени, найдём скорость колебаний:
 , (6.2)
, (6.2)
а вторая производная определяет ускорение колеблющейся точки:
 . (6.3)
. (6.3)
Из
уравнений (6.2) и (6.3) найдём максимальные
значения скорости и ускорения, приравняв
соответственно
 и
и
 к минус единице:
к минус единице:
 , (6.4)
, (6.4)
 . (6.5)
. (6.5)
Из выражения (6.4) найдём циклическую частоту:


и, подставив её в уравнение (6.5) получим:


Определим период колебаний:
 ,
, 
Ответ: 

 .
.
Пример 4.
Материальная
точка массой m=10г
совершает колебания вдоль оси x
около положения равновесия х=0
по закону
![]() Период колебаний Т=1
с, начальная фаза φ0=30°,
максимальная кинетическая энергия
составляет
Период колебаний Т=1
с, начальная фаза φ0=30°,
максимальная кинетическая энергия
составляет![]() =10
мДж. Найти: а) круговую частоту
ω, б) амплитуду
А
колебаний, в) максимальное значение
скорости
,
г) смещение
=10
мДж. Найти: а) круговую частоту
ω, б) амплитуду
А
колебаний, в) максимальное значение
скорости
,
г) смещение
![]() колеблющейся точки в момент времени
t=0.
колеблющейся точки в момент времени
t=0.
Дано Решение
m=10г =10-2кг, Т=1 с , ω=6,28 рад/с, φ=30°,
|
Круговая частота ω находится из соотношения
Так
как период колебаний Т=1
с, тогда
Чтобы найти амплитуду А колебаний, воспользуемся формулой: |
ω ?, А ?,
|
где
скорость
![]() –
первая производная от координаты х,
по времени, т.е.
–
первая производная от координаты х,
по времени, т.е.
![]()
Максимальное
значение скорости
 С учетом этого соотношения выражение
(6.6) принимает вид:
С учетом этого соотношения выражение
(6.6) принимает вид:

Отсюда амплитуда колебаний:

Максимальное значение скорости согласно (1):

Подставляя численные данные, находим А и max:

Величину
смещения
в момент времени t=0
находим из выражения
![]() где начальная фаза φ=30°.
Итак,
где начальная фаза φ=30°.
Итак,
![]()
Подставив численные данные в (6.10), получаем =0,11 м.
Ответ: а) ω=6,28 рад/с; б) А=0,23 м; в) =1,41 м/с; г) =0,11 м.
Пример 5.
Материальная
точка массой 0,01 кг совершает гармонические
колебания, уравнения которых имеют вид:
![]() м. Найти возвращающую силу в момент
времени 0,1 с и полную энергию точки.
м. Найти возвращающую силу в момент
времени 0,1 с и полную энергию точки.
Дано Решение
m= 0,01 кг, t= 0,1 с,
|
Возвращающая сила при гармонических колебаниях определяется следующим выражением
где
|
|
Тогда
Подставляем
численные значения величин, входящих
в формулу для
 из условия задачи, а также из уравнения
колебания: А=
0,2 м,
=8
из условия задачи, а также из уравнения
колебания: А=
0,2 м,
=8![]() рад/с, получаем:
рад/с, получаем:
 (Н).
(Н).
Согласно закону сохранения энергии, полная энергия при колебательном движении будет равна максимальной кинетической энергии:

так
как

Найдем значение полной энергии, подставив в уравнение для Е численные значения:
![]() =
0,126 (Дж).
=
0,126 (Дж).
Ответ:
 Н;
Н;
![]() Дж.
Дж.
Пример 6.
Груз,
подвешенный к спиральной пружине,
колеблется по вертикали с амплитудой
А
= 8 см. Определите жесткость k
пружины, если известно, что максимальная
кинетическая энергия
 груза составляет 0,8 Дж.
груза составляет 0,8 Дж.![]()
Дано Решение
А = 8см = 8·10-2м,
|
В случае гармонических колебаний полная механическая энергия E колебательной системы остается постоянной и равной
|
K – ? |
где
 –
это максимальные кинетическая и
потенциальная энергии груза.
–
это максимальные кинетическая и
потенциальная энергии груза.
Потенциальная энергия и ее максимальное значение определяются по формулам:
 ,
,
где x – растяжение пружины, k – ее жесткость, а xmax – максимальное растяжение пружины, равное амплитуде А колебаний.
Итак,

Отсюда

Ответ:

Пример 7.
Разность
двух фаз одинаково направленных
гармонических колебаний одинакового
периода T
= 4с и одинаковой амплитуды А
= 5см составляет
![]() .
Напишите уравнение движения, получающегося
в результате сложения этих колебаний,
если начальная фаза одного их них равна
нулю.
.
Напишите уравнение движения, получающегося
в результате сложения этих колебаний,
если начальная фаза одного их них равна
нулю.
Дано Решение
T = 4с, A1=A2=5 cм,
|
Запишем уравнения складываемых гармонических колебаний:
|
|
Результирующее колебание имеет вид:
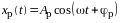 ,
,
где
 –
амплитуда,
–
амплитуда, –
начальная фаза результирующего колебания.
–
начальная фаза результирующего колебания.
Метод
векторных диаграмм дает для
![]() и
и
![]() следующие выражения:
следующие выражения:

По условию задачи A1= A2; ; , поэтому
 ,
,


Найдем частоту колебаний
 .
.
Итак, результирующее колебание будет определяться выражением:

Ответ:

Пример 8.
Точка
участвует в двух гармонических колебаниях,
происходящих во взаимно перпендикулярных
направлениях и описываемых уравнениями
![]() и
и
![]() .
Определите уравнение траектории точки
и вычертите ее с нанесением масштаба.
.
Определите уравнение траектории точки
и вычертите ее с нанесением масштаба.
Дано Решение
,
|
Чтобы найти уравнение траектории точки, нужно исключить параметр t – время из уравнений для x и y. Воспользуемся следующим тригонометрическим тождеством, которое позволяет перейти от двойного угла к обычному углу: |
y = y(x) – ? |
![]()
По
условию задачи
![]() ,
а
,
а
![]() .
Таким образом, траектория движения
точки имеет вид:
.
Таким образом, траектория движения
точки имеет вид:
![]() или
или


Пример 9.
Точка
одновременно совершает гармонические
колебания, происходящие по взаимно
перпендикулярным направлениям и
выражаемые уравнениями
 и
и
 ,
где
,
где
 ,
,
 .
Найдите уравнение траектории и постройте
её, указав направление движения.
.
Найдите уравнение траектории и постройте
её, указав направление движения.
Дано Решение
|
Измерение амплитуд и смещений колебаний целесообразно оставить в сантиметрах. По условию задачи: Исключая
из уравнений (6.11) и (6.12) параметр
, |
|
с
помощью основного тригонометрического
тождества
 ,
получим:
,
получим:
|
|
Траектория
представляет собой эллипс с полуосями
 и
и
 .
.
Направление движения точки по эллипсу определим, построив таблицу (6.1). Время выразим через период колебаний .
Таблица 6.1
-
0




0
0,5
0
- 0,5
0

2
0
- 2
0
2
Ответ: эллипс,
–
 движение происходит по часовой стрелке.
движение происходит по часовой стрелке.
Задача 10.
Определите
период колебаний
математического маятника с длинной
нити
 ,
поднимающегося вверх с ускорением
,
поднимающегося вверх с ускорением

Дано Решение
|
Колебания
маятника, поднимающегося с ускорением
,
эквиваленты колебаниям маятника в
поле силы тяжести с ускорением
|
|
Таким образом, в нашем случае период колебания математического маятника будет определяться так:
 ,
,

Ответ: 
Задача 11.
Тонкий
невесомый стержень длиной
 с грузиками на концах массой
с грузиками на концах массой
 колеблется около горизонтальной оси
(см. рис.). Определите приведённую длину
колеблется около горизонтальной оси
(см. рис.). Определите приведённую длину
 и период колебаний такого маятника,
если расстояние
и период колебаний такого маятника,
если расстояние
 .
.
Дано Решение
|
|
|
Приведённая длина физического маятника
 (6,13)
(6,13)
а период колебаний
 , (6.14)
, (6.14)
где
 –
момент инерции маятника относительно
оси колебаний (точки О). Масса маятника
–
момент инерции маятника относительно
оси колебаний (точки О). Масса маятника
 , (6.15)
, (6.15)
 –
расстояние
от оси вращения до центра инерции
маятника (точки С),
–
расстояние
от оси вращения до центра инерции
маятника (точки С),
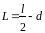 . (6.16)
. (6.16)
Считая
грузики за материальные точки, найдём
момент инерции
 маятника относительно оси вращения
(точки О):
маятника относительно оси вращения
(точки О):
 ,
где
,
где
 ,
,
 ,
поэтому
,
поэтому
 . (6.17)
. (6.17)
Из уравнений (6.13), (6.15) – (6.17) определим приведённую длину маятника:

Приведём вычисление
 .
.
По формуле (6.14) найдём период колебаний маятника:
,


Ответ:  ;
; 
Задачи.
121. Материальная
точка массой
 совершает колебания вдоль оси
совершает колебания вдоль оси
![]() около
положения равновесия
около
положения равновесия
 по закону
по закону .
Амплитуда колебаний составляет
.
Амплитуда колебаний составляет
 см, начальная фаза
см, начальная фаза
 ,
период колебаний
,
период колебаний
 .
В момент времени
.
В момент времени
 найти : а) силу F,
действующую на данную точку, б) кинетическую
энергию
найти : а) силу F,
действующую на данную точку, б) кинетическую
энергию
![]() точки.
точки.
122. Материальная
точка совершает колебания около положения
равновесия по закону
![]() ,
где амплитуда
,
где амплитуда
![]() см,
период колебания
см,
период колебания
![]() с
и начальная фаза
с
и начальная фаза
 .
Найти смещения
.
Найти смещения
![]() и
и
![]() колеблющейся точки от положения
равновесия в моменты времени
колеблющейся точки от положения
равновесия в моменты времени
![]() с
и
с
и
![]() с.
с.
123. Частица
совершает колебания около положения
равновесия по гармоническому закону.
Период колебаний
![]() с.
В момент времени
с.
В момент времени
![]() смещение точки из положения равновесия
смещение точки из положения равновесия
![]() см
и скорость
см
и скорость
![]() м/с.
Найти амплитуду А
колебаний.
м/с.
Найти амплитуду А
колебаний.
103.
Материальная точка совершает колебания
по гармоническому закону около положения
равновесия. Амплитуда колебаний
![]() м,
период колебаний
м,
период колебаний
![]() с.
Найти максимальное значение скорости
с.
Найти максимальное значение скорости
 и ускорение
и ускорение

124. Частица
массой
![]() г
совершает колебания вдоль оси
по
закону
г
совершает колебания вдоль оси
по
закону
 .
При этом максимальное значение
кинетической энергии частицы
.
При этом максимальное значение
кинетической энергии частицы
 Дж.
Найти амплитуду А
колебаний.
Дж.
Найти амплитуду А
колебаний.
125. Тонкий
однородный стержень длиной
![]() см
совершает малые колебания вокруг
горизонтальной оси, перпендикулярной
к стержню и проходящей через его верхний
конец. Момент инерции стержня
см
совершает малые колебания вокруг
горизонтальной оси, перпендикулярной
к стержню и проходящей через его верхний
конец. Момент инерции стержня .
Трения нет. Найти период колебаний.
.
Трения нет. Найти период колебаний.
126. Два
одинаково направленных гармонических
колебания одного периода с амплитудами
![]() см
и
см
и
![]() см
складываются в одно колебание с амплитудой
см
складываются в одно колебание с амплитудой
![]() см.
Найти разность фаз
см.
Найти разность фаз
![]() складываемых колебаний.
складываемых колебаний.
127. Определить
амплитуду
 и начальную фазу
и начальную фазу
![]() результирующего колебания, возникающего
при сложении двух колебаний одинаковых
направления и периода:
результирующего колебания, возникающего
при сложении двух колебаний одинаковых
направления и периода:
 и
и
 ,
где
,
где
![]() см;
см;
![]() с-1;
с-1;
 с.
Найти уравнение результирующего
колебания.
с.
Найти уравнение результирующего
колебания.
128. Складываются
два гармонических колебания одного
направления с одинаковыми периодами
![]() с
и амплитудами
с
и амплитудами
![]() см.
Начальные фазы колебаний
см.
Начальные фазы колебаний
 и
и
 .
Определить амплитуду
.
Определить амплитуду
 и начальную фазу
и начальную фазу
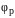 результирующего колебания. Найти его
уравнение.
результирующего колебания. Найти его
уравнение.
129. Максимальная
скорость
![]() точки, совершающей гармонические
колебания, равна 10 см/с, максимальное
ускорение
точки, совершающей гармонические
колебания, равна 10 см/с, максимальное
ускорение
 .
Найти угловую частоту
.
Найти угловую частоту
![]() колебаний, их период
колебаний, их период
![]() и амплитуду
и амплитуду
![]() .
Написать уравнение колебаний, приняв
начальную фазу равной нулю.
.
Написать уравнение колебаний, приняв
начальную фазу равной нулю.
130. Колебания
материальной точки массой
 г
происходят согласно уравнению
г
происходят согласно уравнению
 ,
где
,
где

 Определить
максимальные значения возвращающейся
силы
Определить
максимальные значения возвращающейся
силы
 и кинетической энергии
и кинетической энергии
 .
.
131. Найти
возвращающую силу
в момент
 и полную энергию
материальной точки, совершающей колебания
по закону
где
и полную энергию
материальной точки, совершающей колебания
по закону
где

 Масса
Масса
 материальной точки равна 10 г.
материальной точки равна 10 г.
132. Диск
радиусом
 колеблется около горизонтальной оси,
проходящей через середину одного из
радиусов перпендикулярно плоскости
диска. Определить приведённую длину
колеблется около горизонтальной оси,
проходящей через середину одного из
радиусов перпендикулярно плоскости
диска. Определить приведённую длину
 и период
колебаний такого маятника.
и период
колебаний такого маятника.
133. Математический
маятник длиной
 и физический маятник в виде тонкого
однородного стержня длиной
и физический маятник в виде тонкого
однородного стержня длиной
 синхронно колеблются около одной и той
же горизонтальной оси. Определить
расстояние
синхронно колеблются около одной и той
же горизонтальной оси. Определить
расстояние
 центра масс стержня от оси колебаний.
центра масс стержня от оси колебаний.
134. Физический
маятник представляет собой тонкий
однородный стержень массой
с укреплённым на нём маленьким шариком
массой
.
Маятник совершает колебания около
горизонтальной оси, проходящей через
точку О на стержне. Определить период
гармонических колебаний маятника для
случаев а, б, в, г, изображённых на рис.
6.8. Длина
 стержня равна 1 м. Шарик рассматривать
как материальную точку.
стержня равна 1 м. Шарик рассматривать
как материальную точку.
135. Начальная фаза гармонического колебания равна нулю. Через какую долю периода скорость точки будет равна половине её максимальной скорости.
136. Как изменится период вертикальных колебаний груза, висящего на двух одинаковых пружинах, если от последовательного соединения пружин перейти к параллельному их соединению.
137. Точка
участвует в двух колебаниях одинакового
периода с одинаковыми начальными фазами.
Амплитуда колебаний
 и
и
 Найти
амплитуду результирующего колебания,
если: 1) Колебания совершаются в одном
направлении, 2) Колебания взаимно
перпендикулярны.
Найти
амплитуду результирующего колебания,
если: 1) Колебания совершаются в одном
направлении, 2) Колебания взаимно
перпендикулярны.
138. Точка
участвует одновременно в двух
взаимно-перпендикулярных колебаниях
 и
и
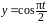 .
Найти траекторию результирующего
движения точки.
.
Найти траекторию результирующего
движения точки.
139. Материальная
точка совершает колебания по гармоническому
закону около положения равновесия.
Амплитуда колебаний
м,
период колебаний
с.
Найти максимальное значение скорости
![]() и
ускорение
и
ускорение
![]()
140. Начальная фаза гармонического колебания равна нулю. При смещении точки от положения равновесия, равном 2,4 см, скорость точки равна 3 см/сек, а при смещении,равном 2,8 см, скорость равна 2 см/сек. Найти амплитуду и период колебания.

 =45°
=45° рад/с,
рад/с,
 –
это первая
–
это первая

 , (6.1)
, (6.1) -
амплитуда колебаний;
-
циклическая частота;
-
начальная фаза.
-
амплитуда колебаний;
-
циклическая частота;
-
начальная фаза.
 =10
мДж
=10
мДж ?,
?
?,
?

 =
0,8 Дж.
=
0,8 Дж.


 –?
–?
 (6.11) (6.11)
(6.11) (6.11) (6.12) (6.12)
(6.12) (6.12)




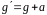 ,
если маятник поднимается вверх, и
,
если маятник поднимается вверх, и
 ,
когда маятник опускается вниз.
,
когда маятник опускается вниз.


