38.Созылуы және сығылу кезіндегі кернеуді анықтау және оның эпюрасын тұрғызыңыз.

КЕРНЕУ

Брус бетіне тік және көлденең бағытта түзулер жүргізейік (Ш.2, а-сурет). Өзара перпендпкуляр бұл түзулер, брусқа күш әсер еткеннен кейін де езара перпендикуляр күйінде қалады (III. 1, б-сурет).

Вертикаль түзулер ұзарады, ал горизонталь түзулер бастапқы орындарын ауыстырып қысқарады. Брустың деформацияға дейінгі жазық көлденең қималары деформациядан кейін де жазық көлденең күйінде қалады. Бұл жорамал Бернуллидің жазық кималар жорамалы деп аталады.

Жасалған тәжірибе, көлденең қималардағы тік кернеулер, қима аудандарында біркелкі жайылып таралып әсер ететінін дәлелдейді. Тік кернеудің шамасын табу үшін, брусты қима әдісі бойынша АВ жазықтығымен қиып, оның төменгі бөлігінің тепе-теңдік теңдеуін құрайық (III.2, в-сурет).

осыдан

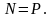
Қимадағы бойлық күш 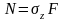болса,

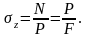III.01

Бойлык күш сияқты, созушы кернеудің таңбасы — оң, ал сығушы кернеудің таңбасы — теріс.

Кернеудің брус бойындағы өзгеру заңдылығын кескіндейтін эпюр ІІІ.2, г-суретте корсетілген.

39.Созылуы және сығылу кезіндегі бойлық және көлденең деформацияларды бағалаңыз (Гук заңы. Пуассон коэффициенті).

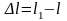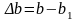Брусты бойлық осінің бойымен созғанда оның ұзындығы шамасына ұзарады (созылады), ал ені шамасына қысқарады (сығылады) (III.3-сурет). Брустың ұзындығының ұзару шамасын абсолюттік ұзару, ал енінің қысқару шамасын абсолюттік қысқару деп атаймыз.

Абсолюттік ұзару шамасының брустың бастапқы ұзындығына қатынасы бойлық салыстырмалы деформация

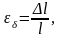
ал қатынасымен анықталатын шама, ендік салыстырмалы деформация делінеді. Салыстырмалы бойлық пен ендік деформациялар арасында мынадай қатынас болатындығы тәжірибе жүзінде дәлелденген

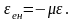III.02

Мұндағы μ— Пуассон немесе ендік деформация коэффициенті деп аталады, ол материалдың қасиетін сипаттайды. Пуассон коэффициентінің мәні әр түрлі материалдар үшін 0-ден 0,5-ке дейін

өзгереді. Тәжірибелердің көрсетулеріне қарағанда барлық серпімді конструкциялық материалдарда пайда болатын деформация кернеуге тура пропорционал

. III.03

Бұл заңдылық Гук заңы деп аталады. Мұндағы Е — материалдың бірінші текті серпімділік модулі, ол тәжірибе жүзінде анықталады. Серпімділік модулі, материал қасиетін сипаттайтын коэффициент; өлшем бірлігі — Н/м².

Енді, және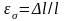 екендігін ескере отырып, (III.03) өрнегін түрлендірейік, сонда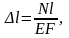 III.04

абсолюттік ұзару үшін Гук заңын аламыз. Мұндағы ЕҒ брустың созылғандағы немесе сығылғандағы қатаңдығы деп аталады.

40-сұрақ. Вектордың абсолют және салыстырмалы туындысы туралы Лемманы қорытыңыз.

Нүктенің күрделі қолғалысын әрі қарай қарастыру кезінде кез келген қозғалыстағы координаттар жүйесіне байланысты анықталған уақыт бойынша туынды алу мәселесі туындайды. Міне, осыған байланысты вектордың абсолют және салыстырмалы туындылары деген ұғымды пайдаланумыз қажет болады. Вектордың анықтамаларына дәне абсолют пен салыстырмалы туындылары арасындағы байланысты табу үшін қозғалмайтын координаттар жүйесі мен қатар, оған қарағанда, лездік бұрыштық жылдамдығы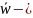 ға тең сфералы ққозғалыс жасайтын Оxyz қозғалмалы координаттар жүйесі дейік. Олардың бас нүктелері полюс О-да болсын. Қандай да уақыт t-ға тәуелді өзгеретін вектор 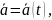қозғалмалы координаттар жүйесіне қатысты алынған вектор болсын. Демек, бұл вектор өзінің қозғалмалы өстердегі проекциялары арқылы жіктелген:

(1)

Мұндағы -векторларын тұрақты векторлар деп алынған туынды (1)-теңдікпен берілген, 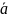векторынан уақыт бойынша алынған туындыны ,векторды ңсалыстырмалы туындысы дейміз. Салыстырмалы туындыны символымен белгілейміз. Сонда бұл анықтаманы өрнектейтін мынадай теңдік аламыз:

(2)

Бұ л формула веторының Оxyz қозғалмалы координаттар жүйесіне қатысты өзгеру тездігін көрсетеді. векторының толық туындысы вектордың абсолют координаттар жүйесіне салыстырып алғандағы өзгеру тездігін анықтайды. Демек, абсолют туындыны есептеу кезінде векторының (1) түрінде берілген жіктелудегі векторының уақыт t-ға тәуелді вектор болып келетіні ескеріледі.

Сонымен (1) теңдікті ңекі жағынан (2)-теңдікті ескере отырып уақыт бойынша туынды аламыз:

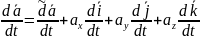(3)

Мұндағы бірлік векторлардан уақыт бойынша алынған туындыларды дене кинематикасында анықталған Эйлер формуласының көмегімен түрлендіреміз:

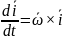
(4)

(4) теңдәктерін(3) теңдігіндегі орындарына қоямыз:

Сонымен, соңғы теңдіктен вектордың абсолюттік туындысы мен салыстырмалы туындысын байланыстыратын мынадай формула аламыз:

(5) (5)-формуланы кинематиканың, вектордың салыстырмалы туындысы жөніндегі леммасы деп атайық. Мұндағы 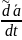вектор -ның салыстырмалы туындысы,ал 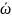- қозғалмалы координаттар жүйесіедегі Оxyz-тің полюс О нүктесі арқылы өтетін өстен айналудың жылдамдығы.

Лемма. Вектордың уақыт бойынша алынған абсолют туындысы сол вектордың салыстырмалы туындысына бұрыштық жылдамдық пен вектордың өзін векторлық түрде көбейтіп алып қосқанға тең (5).

Ескерту. Кинематиканың салыстырмалы туындысы туралы леммасы (1)-теңдік түрдегі жіктелуімен берілген вектордар үшін қолданылады.

41-сұрақ. Созылу және сығылу кезіндегі сырық өсіндегі көлбеу қималардың кернеулерін бағалаңыз.

42-сұрақ. Пластикалық және морт материалдардың созылу диаграммаларын бағалаңыз

Созу диаграммалары

Сан алуан сынау тәсілдерінің ішінде кең тарағаны — материал үлгілерін созуға сынау. Өйткені, созуға сынау нәтижесіңде алынатын механикалық шамалар, материалдардың сыртқы күшке қарсыласу қабілетін, деформациялануын немесе қирау ерекшеліктерін айтарлықтай толық сипаттайды.

Төменгі суретте созу деформациясына сынауға арналған цилиндр пішінді және көлденең қимасы тік төртбұрышты үлгілер көрсетілген (III.6-сурет). Стандарт бойынша цилиндр пішінді үлгілердің есептеу ұзындығы l₀=10d₀, жеке жағдайларда l₀ =5d₀ (III.6, б-сурет). Көлденең қималары тік төртбұрышты үлгілердің есептеу ұзындығы немесе 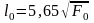(III.6, б-сурет); мұндағы Ғ₀— көлденең қимасының ауданы. Созу деформациясына арналған үлгінің жұмысшы ұзындығы l_ж есептеу ұзындығынан l₀ біршама артық болады. Мысалы, цилиндр пішінді үлгі үшін немесе 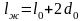жазық үлгі үшін 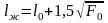немесе

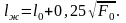
Үлгілер арнайы үзгіш сынау машиналарында сыналады. Бұл машиналар күш пен үлгі деформациясын өлшей алатын аспаптармен қамтамасыз етілген. Сынау кезінде аспаптармен жазылып алынған, күш пен үлгі деформациясының арасыңдағы тәуелділік созу диаграммасы деп аталады.

III.7-суретте аз көміртекті болаттың созу диаграммасы көрсетілген. Диаграмманың абсцисса осіңде үлгінің деформациясы — абсолют созылу шамасы, ал ордината осінде деформацияны тудырушы күш өрнектелген.

Алынған диаграмма P, ∆l координаттары арқылы тұрғызылғандықтан, үлгінің өлшемдеріне тәуелді. Неғүрлым үлгінің диаметрі үлкен болса, оны үзуші күштің шамасы да соғұрлым жоғары болады. Үлгінің есептеу ұзындығы үлкен болған сайын абсолют деформациясының шамасы да үлкен. Бұл тәуелділіктен құтылу үшін ордината осін 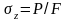арқылы, ал абсцисса осін 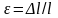арқылы өрнектейді (Ш.8-сурет). Диаграмманың ОА ара-лығының жоғарғы А нүктесіне сәйкес келетін кернеу, материалдың пропорционалдық шегі деп аталып, келесі формуламен анықталады

III.06

Бұл аралықта кернеу мен деформация өзара тура пропорционал, яғни Гук заңына бағынышты.

Қалдық немесе пластикалық деформация тудырмайтын кернеудің ең үлкен шамасы (В нүктесіне сәйкес) серпімділік шегі деп аталып, келесі формуламен анықталады

III.07

Диаграмманың ОА аралығында материал серпімді деформацияланып, деформация кернеуге тура пропорционал өзгерсе, А нүктесі мен В нүктесінің арасында материал серпімді деформацияланғанымен кернеу мен деформацияның арасындағы тура пропорционалдық тәуелділік сақталмайды. Күш әсері В нүктесіне дейін жойылса, серпімді деформация да жойылып, дене, бастапқы қалпына қайта келеді Материалда қалдық деформациясын тудыратын кернеудің ең аз шамасы аққыштық шегі деп аталып, келесі формуламен анықталады

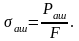III.08

Кернеу шамасы аққыштық шегіне тең болғанда материал пластикалық (қалдық) деформацияға ұшырайды (СD — диаграммаиың аққыштық аралығы). Оның температурасы артып, ток өткізгіштік тағы сол сияқты физикалық қасиеттері өзгереді, үлгінің тегіс бетінде бірқалыпты таралған, бойлық осіне 45° бұрыш жасай өтетін қалың сызықшалар пайда болады. Чернов — Людерс сызықшалары деп аталатын бұл сызықшалар ең үлкен жанама кернеулер әсер ететін жазықтықтарда жатқан кристалдардың өзара ығысу нәтижелері (ІІІ.9, а-сурет), Материал біршама пластикалық деформацияланғаннан кейін, қайтадан сыртқы күш әсеріне қарсыласу қабілетіне ие болып, беріктенеді (DЕ аралығы). Диаграмманың ең жоғаргы нүктесіне сәйкес келетін кернеу беріктік шегі деп аталып, келесі формуламен анықталады

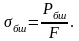III.09

Материалдың беріктік шегін уақытша қарсыласу шегі деп те атайды.

Кернеу шамасы беріктік шегіне жеткенше үлгі өне бойына бірқалыпты созылып, ал жеткеннен кейін оның бойында (қайсыбір жерінде) қылта мойын пайда болады, яғни жіңішкереді (III.9, б-сурет). Әсер етуші сыртқы күштің шамасы төмендей бастайды. Қылта мойын пайда болған аралықта көлденең қима ауданының кішіреюіне байланысты кернеу шамасы өсіп, үлгі үзілуге тақайды.

Үзілу мезетіне сәйкес келетін кернеу шамасы қирау шегі деп аталып, келесі формуламен анықталадм

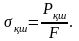III.10

Қарастырылған диаграмма шартты созу диаграммасы деп аталады. Өйткені, бұл диаграммадан алынған материалдың серпімділік, беріктік сипаттамалары σ_пш, σ_сш, σ_аш үлгінің сынауға дейінгі бастапқы қима ауданы Ғ₀ арқылы анықталған. Бірқатар конструкциялық материалдардың механикалық сипаттамалары кітаптың соңындағы 2-кестеде берілген.

Енді_, үлгі үзілгенде, күшті бір-екі рет жойып қайта өсіргендегі созу диаграммасының өзгеру заңдылығын қарастырайық. Әсер етуші сыртқы күш пен үлгіде пайда болған абсолют созылу деформациясының арасыңдағы тәуелділік диаграмманың серпімділік шегіне жетпейтін ОN сызығымен кескінделсін (III.7-сурет). Сыртқы күшті N нүктесіне жеткеннен кейін жойсақ, жою процесінкескіндейтін (азаюшы күш пен деформация арасындағы тәуелділік) сызық, ON сызығымен толық сәйкес келеді. Күш толық жойылғанда үлгідегі деформация да толық жойылады. Күшті, қайта әсер еткізсек, күш пен жаңа деформацияның арасындағы тәуелділік, қатаң түрде созу диаграммасының бастапқы ОN сызығының бойымен өтіп, ары жалғасады.

Ал енді, әсер етуші сыртқы күштің өсуін диаграмманың М нүктесіне жеткен соң тоқтатып, нөлге дейін азайтайық. Азаю кезіндегі күш пен деформацияның арасындағы тәуелділік ОАСВDМ қисық сызығымен кескінделмей, диаграммасының ОА пропорцио-налдық аралығына параллель, МК түзу сызығымен кескіңделеді (III.7-сурет). Диаграмманың М нүктесіне сәйкес келетін, үлгінің толық абсолют созылу деформациясы серпімді созылу мен пластикалық созылу деформацияларының қосындысына тең

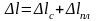немесе

Сыртқы күш толық жойылғанда деформацияның серпімді бөлігі жойылып, үлгіде тек пластикалық (қалдық) деформация қалады. Бұл үлгіге қайтадан сыртқы күш әсер етсе, күш пен деформацияның арасындағы тәуелділік К нүктесінен М нүктесіне дейін пропорционалды түрде өзгеріп, ал одан кейін созу диаграммасының МЕҒ қисық сызығының өзгеру заңдылығымен сәйкес келеді.

Сонымен, қайтадан деформацияланған үлгінің пропорционалдық шегі алдыңғы әсер еткен Р_мкүшінің шамасына дейін өсіп, беріктік қасиеті артады, ал пластикалық қасиеті кемиді. Бұл құбылыс "Материалдар кедергісі" ғылымында беріктену деп аталады. Машина жасау өндірісінде материалдарды беріктендіріп пластикалық қасиетін төмендету үшін, оларды алдын ала деформациялап шынықтыру әдісі кеңінен қолданылады.

Материалдың пластикалық қасиеті оның қалдық салыстырмалы созылуымен немесе жіңішкеруімен сипатталады.

Қалдық салыстырмалы созылу

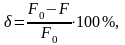III.11

мұндағы l₀, l — үлгінің сынауға дейінгі және сынаудан кейінгі ұзындықтары.

Қалдық салыстырмалы жіңішкеру

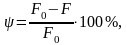
мұндағы F₀, F — үлгінің көлденең қимасының деформацияға дейінгі және үзілгеннен кейінгі ең кіші аудандары.

Созу диаграммасындағы аққыштық аралық (СD) тек пластикалық материалдарға тән. Пластикалық материалдарға, қирау мезетіне сәйкес келетін деформациясы 15—20%-тен кем емес аз көміртекті болаттар, мыс, алюмииний сияқты металдар, олардың ерітпе түрлері жатады. Кейбір пластикалық материалдардың диаграммаларында аққыштық аралық байқалмайды.

Қирау мезетінде деформация шамасы 2—5%-тен аспайтын жоғары көміртекті болаттар, шойын, тас, бетон, шыны сияқты т. б. материалдар морт материалдар деп ажыратылады. III.10-суретте шойынның созу диаграммасы көрсетілген. Диаграммаға қарап, барлық морт материалдарға тән, кернеу мен деформацияның арасындағы тәуелділік тура пропорционал емес қисық сызықты екенін байқауға болады. Диаграммадан алынатын сипаттама біреу-ақ — ең жоғарғы нүктесіне сәйкес келетін беріктік шегі (уақытша қарсыласу шегі).

Сырттан әсер етуші күшті беріктік шегіне жеткізбей жойса, онда материалда пайда болған деформация да толығымен жойылып кетеді, яғни морт материалдар серпімді деформацияланады. Көп жағдайларда қисық сызықты созу диаграммасы түзу сызықпен алмастырылады (III.10-сурет).

Морт материалдарды қатаңдыққа немесе беріктікке есептегенде, кернеу мен деформация арасындағы байланыс Гук заңына бағынышты деп қарастырылады. Өзара бірдей, морт материалдан жасалынған үлгілердің беріктік шектері өзара бірдей болмауы мүмкін. Ал пішіндері мен өлшемдері бірдей емес үлгілердің беріктік шектерінің әр түрлі болуы күмәнсыз. Мысалы, өлшемдері үлкен үлгінің беріктік шегі өлшемдері кіші үлгінің беріктік шегінен кіші. Яғни құрылым ерекшеліктеріне байланысты, морт материалдарға масштаб факторы айтарлықтай әсерін тигізеді.