
- •10. Қатты дененің қозғалмайтын өс төңірегіндегі айналмалы қозғалысына анықтама беріңіз және оны зерттеу әдісін түсіндіріңіз.
- •11.Қатты дененің жазық параллель қозғалысының заңы, оны анықтау тәсілдері қандай?
- •38.Созылуы және сығылу кезіндегі кернеуді анықтау және оның эпюрасын тұрғызыңыз.
- •39.Созылуы және сығылу кезіндегі бойлық және көлденең деформацияларды бағалаңыз (Гук заңы. Пуассон коэффициенті).
- •43.Созылу және сығылу кезіндегі потенциалдық энергия. Мүмкіндік кернеу. Беріктіктің қор коэфициентін бағалаңыз.
- •53.Қималардың инерция моменттері және оларды анықтау.
-
№
Сұрақ
Блок
1
Нүкте кинематикасыда қаралатын мәселелер. Кеңістік, уақыт және санақ жүйесіне түсінік беріңіз.
1
2
Векторлық тәсілмен берілген нүкте қозғалысының координаталық тәсілден ерекшелігі және осы тәсілмен нүктенің кинематикалық параметрлерін анықтаңыз.
1
3
Координаталық тәсілмен берілген нүкте қозғалысының табиғи тәсілден ерекшелігі және осы тәсілмен нүктенің кинематикалық параметрлерін анықтаңыз.
1
4
Табиғи тәсілмен берілген нүкте қозғалысының векторлық тәсілден ерекшелігі және осы тәсілмен нүктенің кинематикалық параметрлерін анықтаңыз.
1
5
Үдеу векторларын табиғи өстерге жіктеуді түсіндіріңіз.
1
6
Нүкте қозғалысының кейбір жеке түрлерін толық сипаттаңыз.
1
7
Нүктенің шеңбер бойымен қозғалысындағы толық үдеуін қорытыңыз.
1
8
Жылдамдықтарды қосу туралы теореманы тұжырымдаңыз және оның қажеттілігін түсіндіріңіз .
1
9
Қатты дененің ілгерілемелі қозғалысын түсіндіріңіз және оған мысал келтіріңіз.
1
10
Қатты дененің қозғалмайтын өс төңірегіндегі айналмалы қозғалысына анықтама беріңіз және оны зерттеу әдісін түсіндіріңіз.
1
11
Қатты дененің жазық параллель қозғалысының заңы, оны анықтау
тәсілдері қандай?
1
12
Қатты дененің қозғалмайтын нүкте төңірегіндегі қозғалысына сипаттама беріңіз. Эйлер бұрыштарының мағынасын түсіндіріңіз.
1
13
Еркін қатты дене қозғалы. Эйлер-Шаль теоремасының мағынасын түсіндріңіз.
1
14
Нүктенің күрделі (абсолют) қозғалысын түсіндіріңіз және оның теңдеулері қандай? Күрделі қозғалыстағы нүктенің кинематикалық парметрлерін анықтаңыз.
1
15
Статика мәселелері мен оның негізгі аксиомалары қандай? Күш және масса ұғымын түсіндіріңіз.
1
16
Байланыстар. Байланыстар реакцияларын түсіндіріңіз.
1
17
Күштің нүктеге қатысты моменттерінің скалярлық және векторлық анықтамаларын беріңіз.
1
18
Күштің өске қатысты моменттері. Күштің нүктеге және өске қатысты моменттерін координаттық әдіспен есептеу.
1
19
Бір нүктеге түсірілген күштер жүйесі және олардың тең әсер етушісін анықтау тәсілдері.
1
20
Жинақталушы күштер жүйесі. Жинақталушы күштер жүйесінің тепе-теңдік шарты мен теңдеулерін жазыңыз.
1
21
Өзара паралель емес үш күштер туралы теорема және оның мағынасын сипаттаңыз.
2
22
Қос күштер туралы түсінік. Қос күштер моменті. Қос күштер жүйесінің тепе теңдік шарттарын сипаттаңыз.
2
23
Динамиканың мәселелері, негізгі түсініктері мен ұғымдары. Нүкте қозғалысының дифференциал теңдеулерiн сипаттаңыз (барлық түрлері).
2
24
Материалық нүкте динамикасының жалпы теоремаларын сипаттаңыз.
2
25
Полярлық координаталардағы нүкте үдеуін қорытыңыз.
2
26
Тороидтық координаталардағы нүкте үдеуін қорытыңыз.
2
27
Цилиндрлік кординаталардағы нүкте үдеуін қорытыңыз.
2
28
Нүктенің қозғалу заңы
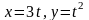 теңдеулерімен
берілген. Екі секундтан кейін нүкте
координаталар жүйесінің бас нүктесінен
қандай қашықтықта болады?
теңдеулерімен
берілген. Екі секундтан кейін нүкте
координаталар жүйесінің бас нүктесінен
қандай қашықтықта болады?2
29
Нүктенің қозғалу заңы
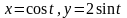 теңдеулерімен
берілген. t
=2,5 с
болған сәтте нүкте координаталар
жүйесінің бас нүктесінен қандай
қашықтықта болады?
теңдеулерімен
берілген. t
=2,5 с
болған сәтте нүкте координаталар
жүйесінің бас нүктесінен қандай
қашықтықта болады?
2
30
Нүктенің қозғалу заңы
 теңдеулерімен
берілген. Қанша уақыттан кейін нүкте
координаталар жүйесінің бас нүктесінен
10
м
қашықтықта болады?
теңдеулерімен
берілген. Қанша уақыттан кейін нүкте
координаталар жүйесінің бас нүктесінен
10
м
қашықтықта болады?2
31
Автомобильдің жылдамдығы 12 с ішінде нольден 60 км/сағ-қа дейін бірқалыпты өседі. Автомобильдің үдеуін анықтаңыз.
2
32
Сфералық координаталардағы нүкте жылдамдығын қорытыңыз.
2
33
Тороидтық координаталардағы нүкте үдеуін қорытыңыз.
2
34
Сыртқы күштер және олардың түрлерін сипаттаңыз
2
35
Қималар әдісін және оның қажеттілігін түсіндіріп, сипаттаңыз.
2
36
Деформация және кернеу ұғымын түсіндіріңіз. Олардың теңдеулерін сипаттаңыз.
2
37
Тік білеудің созылуы және сығылуы. Созылуы және сығылу кезіндегі бойлық күшті анықтау және оның эпюрасын тұрғызыңыз.
2
38
Созылуы және сығылу кезіндегі кернеуді анықтау және оның эпюрасын тұрғызыңыз.
2
39
Созылуы және сығылу кезіндегі бойлық және көлденең деформацияларды бағалаңыз (Гук заңы. Пуассон коэффициенті).
2
40
Вектордың абсолют және салыстырмалы туындысы туралы Лемманы қорытыңыз.
2
41
Созылу және сығылу кезіндегі сырық өсіндегі көлбеу қималардың кернеулерін бағалаңыз.
3
42
Пластикалық және морт материалдардың созылу диаграммаларын бағалаңыз.
3
43
Созылу және сығылу кезіндегі потенциалдық энергия. Мүмкіндік кернеу. Беріктіктің қор коэфициентін бағалаңыз.
3
44
Созылған және сығылған білеуді беріктікке есептеу түрлері.
3
45
Нүктедегі кернеулі күй және оның түрлері. Жанама кернеулердің жұптық заңын бағалаңыз.
3
46
Кариолис теоремасын қорытыңыз.
3
47
Еркін қатты дене үшін үдеудің құраушыларын қозғалмалы координат жүйесі үшін қорытып беріңіз
3
48
Сыртқы және ішкі күштердің жұмысы. Созу (сығу) деформациясының потенциалдық энергиясын бағалаңыз.
3
49
Ығысу. Ішкі күштер. Таза ығысу кезіндегі Гук заңын түсіндіріңіз.
3
50
Еркін қатты дене үшін үдеудің құраушыларын қозғалмайтын координат жүйесі үшін қорытып беріңіз
3
51
Бұралу бұрышын анықтау. Бұралған біліктерді беріктік пен қатаңдыққа есептеу.
3
52
Қималардың геометриялық сипаттамалары. Қималардың статикалық моменттерін бағалаңыз.
3
53
Қималардың инерция моменттері және оларды анықтау.
3
54
Арқалықтың иілуі туралы түсінік. Жанама күш пен июші моментті сипаттаңыз.
3
55
Таза иілу. Иілу кезіндегі кернеулерді анықтаңыз.
3
56
Суретте көрсетілген болат сырыққа
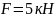 ,
,
 ,
,
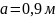 ,
,
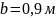
 ,
,
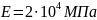 жүктемелер әсер етеді. Осы жүктемелердің
әсерінен пайда болатын бойлық күштің,
тік кернеудің эпюрасын тұрғызыңыз.
жүктемелер әсер етеді. Осы жүктемелердің
әсерінен пайда болатын бойлық күштің,
тік кернеудің эпюрасын тұрғызыңыз.
2
57
Суретте көрсетілген болат сырыққа
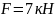 ,
,
 ,
,
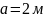 ,
,
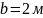 ,
жүктемелер әсер етеді. Осы жүктемелердің
әсерінен пайда болатын бойлық күштің,
тік кернеудің және абсолюттік орын
ауыстырудың эпюрасын тұрғызыңыз.
,
жүктемелер әсер етеді. Осы жүктемелердің
әсерінен пайда болатын бойлық күштің,
тік кернеудің және абсолюттік орын
ауыстырудың эпюрасын тұрғызыңыз.
2
58
Суретте көрсетілген болат сырыққа
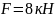 ,
,
 ,
,
,
,
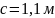 ,
жүктемелер әсер етеді. Осы жүктемелердің
әсерінен пайда болатын бойлық күштің,
тік кернеудің және абсолюттік орын
ауыстырудың эпюрасын тұрғызыңыз.
,
жүктемелер әсер етеді. Осы жүктемелердің
әсерінен пайда болатын бойлық күштің,
тік кернеудің және абсолюттік орын
ауыстырудың эпюрасын тұрғызыңыз.
2
59
Суретте көрсетілген болат сырыққа
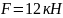 ,
,
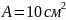 ,
,
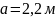 ,
,
 ,
,
жүктемелер әсер етеді. Осы жүктемелердің
әсерінен пайда болатын бойлық күштің,
тік кернеудің және абсолюттік орын
ауыстырудың эпюрасын тұрғызыңыз.
,
,
жүктемелер әсер етеді. Осы жүктемелердің
әсерінен пайда болатын бойлық күштің,
тік кернеудің және абсолюттік орын
ауыстырудың эпюрасын тұрғызыңыз.
2
60
Суретте көрсетілген болат сырыққа
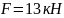 ,
,
,
,
 ,
,
 ,
,
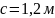 ,
жүктемелер әсер етеді. Осы жүктемелердің
әсерінен пайда болатын бойлық күштің,
тік кернеудің және абсолюттік орын
ауыстырудың эпюрасын тұрғызыңыз.
,
жүктемелер әсер етеді. Осы жүктемелердің
әсерінен пайда болатын бойлық күштің,
тік кернеудің және абсолюттік орын
ауыстырудың эпюрасын тұрғызыңыз.
2
1-сұрақ. Нүкте кинематикасыда қаралатын мәселелер. Кеңістік, уақыт және санақ жүйесіне түсінік беріңіз.
Жалпы алғанда механикалық денелердің қозғалысы өте күрделі,өйткені ол қарастырып отырған денелердің формасына,өлшеміне және тағы басқа қасиеттеріне байланысты.Осы себептен денелер қозғалысын қарастырған кезде сол денелердің кейбір қасиеттерін ескермеуге болатындай жорамал жасалады,басқаша айтқанда механикалық денелердің моделін енгізу керек.Оларға мыналар жатады:
Материалдық нүкте-қарастырып отырған есептің шартына байланысты өлшемдерін ескермеуге болатын дене.Мысалы:күнді айналып жүрген жерді материалдық нүкте ретінде есептеуге болады,себебі траекторияның радиусы жердің радиусынан өте үлкен.
Материалдық нүктелер жүйесі-механикалық денелер жиынтығын материалдық нүктелер жүйесі деп атауға болады,егер әр бір денені материалдық нүкте деп қарастыруға болады.
Материалдық нүктелер жүйесі механикалық жүйе деп қарастыруға болады,егер әрбір нүктенің қозғалысы басқа қалған нүктелерге тәуелді болса.
Механикалық жүйені абсолюттік қатты дене деп атаймыз,егер кез келген екі нүктенің ара қашықтығы қозғалыс кезінде өзгермейтін болса.
Тұтас орта-газдар,сұйықтықтар.
Кеңістік пен уақыт ұғымдары
Классикалық механикада денелердің баяу қозғалысы қарастырылатындықтан,тәжірибелердің нәтижелерін салыстыра отырып,кеңістік пен уақыт ұғымдарын анықтама бере аламыз.
Кеңістік- үздіксіз,біртекті және изотропты,ал оның өлшемдері эвклид геометриясының аксиомаларымен сипатталады.
Уақыт- кеңістіктің кез келген бөліктеріне біркелкі таралады да,үздіксіз және біртекті.
Денелердің механикалық қасиеттері кеңістіктің кез келген бөлігінде және кез келген уақыт мезетінде өзгермейтін болса,ондай кеңістікті және уақытты біртекті деп атаймыз.
Санақ жүйесі
Кез келген материалдық нүктенің қозғалысын анықтау үшін басқа бір дене таңдап алып осы денеге қатысты,қарастырып отырған нүктенің қозғалысын сипаттау керек. Осындай денемен байланысқан тік бұрышты үшбұрышты координаттар жүйесімен,уақытты есептеу үшін керекті сағаттан тұратын жүйені санақ жүйесі дейміз.
Классикалық механикада қозғалыс заңдарын қарастырған кезде мынадай 3 постулатты негізігі алады:
1.Механикалық қозғалысты сипаттайтын кез келген физикалық шамаларды бір уақыт мезетінде өлшеуге болады.Басқаша айтқанда өлшеуіш приборлардың өлшенетін физикалық шамаға тигізетін әсерін ескермеуге болады.
2.Белгілі бір механикалық процестің өтетін уақыты кез келген қозғалыстағы санақ жүйелерінде бірдей болады,яғни t2-t1=t2-t1 мұндағы (t2-t1), (t2-t1) екі санақ жүйесіне қатысты процестің өту уақыты.
3.Кез келген қозғалыстағы санақ жүйелерінде механикалық денелердің ара қашықтығы бірдей болады,r͞₁₂=r͞₁₂.
Бұдан кез келген екі нүктенің ара қашықтығы,кез келген санақ жүйесіне қатысты өзгермейтінін көреміз
(dr)²=(dx)²+(dy)²+(dz)²= тұр
Осы постулаттың 3-де тек классикалық механикада орындалады.
2-cұрақ. Векторлық тәсілмен берілген нүкте қозғалысының координаталық тәсілден ерекшелігі және осы тәсілмен нүктенің кинематикалық параметрлерін анықтаңыз.
Қозғалып бара жатқан нүктенің кеңістікте қалдыратынізі траектория депаталады. Траектория түзуден тұратын болса, түзу сызықты қозғалыс, қисық сызықтан тұратын болса, қисық сызықты қозғалыс делінеді. Егер таңдалған санақ жүйесіне қатысты нүктенің орнын анықтау тәсілі көрсетілген болса, нүкте қозғалысы берілген деп есептелінеді.
Материялық нүктеқозғалысы 4 тәсілменберіледі:
1) векторлық; 2) координаталық; 3) табиғи; 4) полярлық. Бізнегізіндеүштәсілментанысамыз.

1.
Векторлықтәсіл. Айталық, М
нүктеОхуzкординаттаржүйесінеқатысты
АВ траектория бойыменқозғалыстаболсын.
О және М нүктелердібіріктіретін
вектор![]() =
=![]() нүктенің
радиус-векторы делінеді (8.1сурет).
нүктенің
радиус-векторы делінеді (8.1сурет).
8.1сурет
Уақыт өтуімен М нүктенің алған орны өзгеріп отырады. Нәтижеде оның радиус-векторының ұзындығы мен бағыты өзгереді. Егер М нүктенің радиус-векторы уақыттың функциясы ретінде берілген болса, нүктенің кеңістіктегі орны кез-келген уақыт үшін анықталған болады, яғни
![]()
 (8.1)
(8.1)
Демек (1.1) нүкте қозғалысының вектор тәсілінде берілгендегі теңдеуі.
3-сұрақ. Координаталық тәсілмен берілген нүкте қозғалысының табиғи тәсілден ерекшелігі және осы тәсілмен нүктенің кинематикалық параметрлерін анықтаңыз.
Координаталық тәсіл. Сызба геометриядан және математикадан белгілі болған нәрсе, ол қозғалып бара жатқан М нүктесінің кез-келген уақыттағы алатын орнын х, у, z Декарт координаттары арқылы анықтау мүмкіндігі. Нүкте қозғалғанда координаттар уақыт өтуімен өзгереді, яғни олар уақыттың бір мәнді функциясы болады:
x=x(t), y=y(t), z=z(t) (8.2)
Бізге (8.2) өрнегі белгілі болса, онда нүктенің кеңістіктегі алған орнын кезкелген уақытта анықтау мүмкін.
Олай болса (8.2) теңдеуі нүкте қозғалысының координат тәсіліндегі берілуін анықтайды.
Егер (8.2) өрнектен уақытты жойсақ, нүктенің траектория теңдеуі келіп шығады. М нүктеқозғалысыжазықтықтаорыналса, (8.2) төмендегідейболады:
x=x(t), y=y(t) (8.3)
Нүкте қозғалысы түзу сызықты болса, онда қозғалыс бағытын Ох өсіменбағыттасдеп, (8.2) өрнекті
x=x(t) (8.4)
түрінде жазуға болады.
Егер Охуz координат
жүйесі өстерінің бірлік бағыттаушы
векторларын сәйкес түрде  десек, М нүктенің
радиус-векторын төмендегідей жазу
мүмкін (8.1 сурет):
десек, М нүктенің
радиус-векторын төмендегідей жазу
мүмкін (8.1 сурет):
![]()
 (8.5)
(8.5)
Анықталған (8.5) теңдеуі нүкте қозғалысының вектор тәсілінде берілуімен нүкте координаттары арасындағы қатынасты өрнектейді.
4-сұрақ. Табиғи тәсілмен берілген нүкте қозғалысының векторлық тәсілден ерекшелігі және осы тәсілмен нүктенің кинематикалық параметрлерін анықтаңыз.
Табиғи тәсіл. Айталық, М нүкте АВ траектория бойымен қозғалыста болсын (8.2 сурет). Траекториядағы кезкелген О нүктені санақ орталығы (центрі) деп, оң және теріс бағыттарды белгілеп аламыз. Онда нүктенің траекториядағы орны S қисық сызықты координатпен анықталады, яғни
![]()
 (8.6)
(8.6)

8.2 сурет
Демек (8.6) теңдеуі М нүктенің траектория бойымен жылжығандағы қозғалыс заңын немесе табиғи тәсілде оның берілуі болады.
Сонымен, М нүктенің қозғалысын табиғи тәсілде анықтау үшін 1) траектория; 2) траекториядағы санақ центрі; 3) қозғалыс бағыты; 4) таректория бойымен қозғалыс заңы берілуі керек. Көрініп тұрғандай, траектория белгілі болса, қойылған мәселені шешкен кезде осы тәсілден пайдалану керек.
5-сұрақ. Үдеу векторларын табиғи өстерге жіктеуді түсіндіріңіз.
1.
Табиғи
үш жақ.Табиғи өстер.Траекторияның
бір-біріне шексіз жақын орналасқан үш
нүктесі арқылы өтетін жазықтық , оның
ортаңғы нүктесіне жүргізілген , жанаспа
жазықтық деп аталады. Жанамаға
перпендикуляр , М нүктесі арқылы өтетін
, N- жазықтығы траекторияның осы нүктедегі
нормаль жазықтығы деп аталады.Траекторияның
М нүктесіндегі жанама арқылы өтетін
нормаль және жанаспа жазықтықтарға
перпендикуляр үшінші жазықтық
траекторияның сол нүктедегі түзулеуші
жазықтыңы деп аталады.(1-сурет)-Жанаспа
жазықтықта жатқан нормаль , қисықтың
М-нүктесіндегі бас нормаль деп, ал
жанаспа жазықтыққа осы нүктеде жүргізілген
перпендикуляр бинормаль деп
аталады
.Бас нүктесі координаттар жүйесі М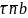 табиғи
координаттар жүйесі
деп , немесе табиғи
үш жақ деп аталады .Координаттар
жазықтары екі-екіден алынған бірлік
векторларымен анықталады.(
табиғи
координаттар жүйесі
деп , немесе табиғи
үш жақ деп аталады .Координаттар
жазықтары екі-екіден алынған бірлік
векторларымен анықталады.( ,
,
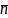 )-жанаспа
жазықтық.
(
)-жанаспа
жазықтық.
( b)-нормаль жазықтық .(
b)-нормаль жазықтық .(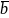 ,
)-түзулеуші
жазықтық.
,
)-түзулеуші
жазықтық.
2.Қисық сызық қисықтығы . Нүктенің траекториясын жалпы жағдайда кеңістіктегі қисық сызық деп санаймыз. Нүкте траекториясының М нүктесі берілсін .Траекторияның осы нүктесінде
Және
оған жақын орналасқан екінші нүктесі
 арқылы
және
1
жанама
бірлік векторын жүргізейік(2-сурет).М1нүктесі
берілген М нүктесінен ΔS қашықтықта
болсын,
1
векторын М-нүктесіне параллель көшірейік.М
нүктесіндегі
және
1екі
бірлік векторлар арасындағы бұрышты
Δθ деп белгілейік .Бұл бұрыштың ΔS доға
бұрышына қатынасын алайық:
арқылы
және
1
жанама
бірлік векторын жүргізейік(2-сурет).М1нүктесі
берілген М нүктесінен ΔS қашықтықта
болсын,
1
векторын М-нүктесіне параллель көшірейік.М
нүктесіндегі
және
1екі
бірлік векторлар арасындағы бұрышты
Δθ деп белгілейік .Бұл бұрыштың ΔS доға
бұрышына қатынасын алайық:
 =kорт
(1)
=kорт
(1)
(1)қатынасын траекторияның ММ1 доғасының орташа қисықтығы дейміз.
Қисықтың берілген М нүктесіндегі қисықтығы деп орташа қисықтықтың ΔS нөлге ұмтылғандағы шегіне тең шаманы айтады:
 орт
=k
(2)
орт
=k
(2)
Орташа қисықтың өрнегі (1)арқылы (2)теңдігін мына түрде жазайық;
 =k
(3)
=k
(3)
K= (4)
(4)
формула қисық сызықтың берілген М
нүктесіндегі қисықтығын аныктайды .Ол
былай айтылады .Траекторияның берілген
нүктесіндегі қисықтығы элементар
сыбайластық бұрыштың доға элементіне
қатынасына тең шама.
3. Қисықтың
берілген нүктедегі қисықтық
радиусы.
Қисықтың М нүктесі берілсін,
оның осы М нүктесіндегі қисықтық радиусы
деп осы нүктедегі k-ға кері шаманы
айтады.Қисықтың берілген М нүктесіндегі
қисықтық радиусы p десек , онда ол осы
айтылған анықтама бойынша мынаған тең;
(4)
(4)
формула қисық сызықтың берілген М
нүктесіндегі қисықтығын аныктайды .Ол
былай айтылады .Траекторияның берілген
нүктесіндегі қисықтығы элементар
сыбайластық бұрыштың доға элементіне
қатынасына тең шама.
3. Қисықтың
берілген нүктедегі қисықтық
радиусы.
Қисықтың М нүктесі берілсін,
оның осы М нүктесіндегі қисықтық радиусы
деп осы нүктедегі k-ға кері шаманы
айтады.Қисықтың берілген М нүктесіндегі
қисықтық радиусы p десек , онда ол осы
айтылған анықтама бойынша мынаған тең;
P=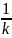 (5)
4.Үдеу
векторының жанама және нормаль
құраушылары.
Кеңістікте бойымен М
нүктесі қозғалатын қисық берілсін.
Нүктенің траектория бойындағы М орнына
S=O1M
доғасына сәйкес келеді (4-сурет).Бұл
доғаның t-уақытқа тәуелділігі берілсін;
S=f(t) (6)
Қозғалыс
заңы (6)теңдігі түрінде берілген М
нүктесінің үдеуінің векторы
(5)
4.Үдеу
векторының жанама және нормаль
құраушылары.
Кеңістікте бойымен М
нүктесі қозғалатын қисық берілсін.
Нүктенің траектория бойындағы М орнына
S=O1M
доғасына сәйкес келеді (4-сурет).Бұл
доғаның t-уақытқа тәуелділігі берілсін;
S=f(t) (6)
Қозғалыс
заңы (6)теңдігі түрінде берілген М
нүктесінің үдеуінің векторы
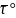 арқылы
өрнектейік:
арқылы
өрнектейік:
 =v
ₒ
=v
ₒ
6-сұрақ. Нүкте қозғалысының кейбір жеке түрлерін толық сипаттаңыз
Траекторияның түріне қарай нүкте қозғалысы екі топқа бөлінеді. Қозғалыс кезінде түзу сызық сызатын нүктені түзу сызықты қозғалыс жасайды дейміз, траекториясы қисық сызық түрінде болып келетін нүктені екінші топқа жатқызамыз. Нүкте жылдамдығының өзгеруіне қарап бұл екі топтағы нүкте қозға-лыстарының әрқайсысын әр түрге бөліп атаймыз. Алдымен нүктенің түзу сызықты қозғалысына жеке тоқтап өтейік.
1.
Түзу сызықты
бірқалыпты қозғалыс.
Түзудің
қисық-тық радиусы
![]() болғандықтан түзу сызықты қозғалыс-тағы
нүктенің нормаль үдеуі нөлге тең болады
да, оның толық үдеуі жанама құраушысына
тең болады:
болғандықтан түзу сызықты қозғалыс-тағы
нүктенің нормаль үдеуі нөлге тең болады
да, оның толық үдеуі жанама құраушысына
тең болады:
 .
(2.50)
.
(2.50)
Нүктенің жылдамдығы тұрақты, түзу сызықты қозғалысы – түзу сызықты бірқалыпты қозғалыс деп аталады. Мұндай қозғалыстың (2.50) – формула бойынша үдеуі нөлге тең болады да, қозғалыс кезіндегі уақыттардың бәрінде жылдамдық векто-ры модулін өзгертпей сақтайды.
Түзу сызықты, бірқалыпты қозғалысты сипаттайтын формулалар мынадай:
![]()
![]()
![]() .
(2.51)
.
(2.51)
2. Түзу сызықты бірқалыпты айнымалы қозғалыс. Үдеуі тұрақты нүктенің түзу сызықты қозғалысы – бірқалыпты айнымалы қозғалысы деп аталады, мұндай қозғалысты сипаттай-тын формулалар элементар физикадан белгілі:
![]()
![]()
 .
(2.52)
.
(2.52)
3.
Қисық
сызықты бірқалыпты қозғалыс.
Нүктенің
қисық сызықты қозғалысында
![]() болса, онда ол бірқалыпты
қисық сызықты
қозғалыс деп
аталады. Демек, бірқалыпты қисық сызықты
қозғалыс кезінде нүктенің жанама үдеуі
нөлге тең болады да, толық үдеуі өзінің
нормаль құраушысына тең болып келеді.
Қисық сызықты бірқалыпты қозғалысты
сипаттайтын формулалар мына түрде
жазылады:
болса, онда ол бірқалыпты
қисық сызықты
қозғалыс деп
аталады. Демек, бірқалыпты қисық сызықты
қозғалыс кезінде нүктенің жанама үдеуі
нөлге тең болады да, толық үдеуі өзінің
нормаль құраушысына тең болып келеді.
Қисық сызықты бірқалыпты қозғалысты
сипаттайтын формулалар мына түрде
жазылады:
![]() ,
,
 .
(2.53)
.
(2.53)
Нүкте жылдамдығын өрнектейтін теңдеуді интегралдау арқылы бірқалыпты қисық сызықты қозғалыс заңын табамыз:
![]() .
(2.54)
.
(2.54)
4. Қисық сызықты бірқалыпты айнымалы қозғалыс. Нүктенің жанама үдеуі қозғалыс кезінде үнемі тұрақты, яғни:
![]() ,
(2.50)
,
(2.50)
болса, онда қисық сызықты қозғалыс бірқалыпты айнымалы қозғалыс деп аталады. Мына теңдікті түрлендіре отырып оны мына түрде жазайық:
![]() .
(2.55)
.
(2.55)
Осы теңдеуді интегралдау арқылы қозғалыс жылдамды-ғының өзгеру заңын табамыз:
![]() ,
(2.56)
,
(2.56)
мұндағы, ν0 нүктенің t0=0 болған кездегі бастапқы жылдамдығы. Қисық сызықты бірқалыпты айнымалы қозғалыс заңын:
![]() .
(2.57)
.
(2.57)
Теңдеуін интегралдау арқылы мына түрде аламыз:
 ,
(2.58)
,
(2.58)
мұндағы, S0 – бастапқы қашықтық.
5.
Қисық сызықты қозғалыстың жалпы жағдайы.
Үдеу
векторы жылдамдық векторының өзгеру
тездігін анықтайды. Ол жалпы жағдайда
жанама және нормаль құраушыларға
жікте-леді. Жанама үдеу жылдамдық
векторының сан мәнінің өзге-руін, ал
нормаль үдеу жылдамдық бағытының
өзгеруін сипат-тайды. Жалпы жағдайда,
жылдамдықтың өзгеруі толығынан
қарастырылатындықтан
![]() ,
,
![]() болып келеді.
болып келеді.
Жалпы
жағдайдағы қисық сызықты қозғалыс
үдемелі және кемімелі деген екі түрге
бөлінеді. Үдемелі қозғалыс кезінде
![]() және
және
![]() шамаларының таңбалары бірдей, ал кемімелі
қозғалыс кезінде бұлардың таңбалары
қарама-қарсы болып келеді. Басқаша
айтқанда, үдемелі қозғалыс кезінде
жанама үдеу векторы жылдамдық векторымен
бірдей бір жаққа қарай бағытталады, ал
кемімелі қозғалыс кезінде ол жылдамдық
векторына қарама-қарсы бағытта болады.
шамаларының таңбалары бірдей, ал кемімелі
қозғалыс кезінде бұлардың таңбалары
қарама-қарсы болып келеді. Басқаша
айтқанда, үдемелі қозғалыс кезінде
жанама үдеу векторы жылдамдық векторымен
бірдей бір жаққа қарай бағытталады, ал
кемімелі қозғалыс кезінде ол жылдамдық
векторына қарама-қарсы бағытта болады.
 оң
шама болғандықтан нормаль үдеу бас
нормальмен бірдей бағытталады. Нормаль
үдеу траекторияның қисықтық центріне
қарай бағытталуына байланысты, ол кейде
центрге ұмтылғыш үдеу деп те аталынады.
Осыдан, бұрын айтылған үдеу векторының
үнемі траекторияның ойыс жағына қарай
бағытталатындығын, нормаль үдеу туралы
берілген осы түсінік, оны айқындай
түседі.
оң
шама болғандықтан нормаль үдеу бас
нормальмен бірдей бағытталады. Нормаль
үдеу траекторияның қисықтық центріне
қарай бағытталуына байланысты, ол кейде
центрге ұмтылғыш үдеу деп те аталынады.
Осыдан, бұрын айтылған үдеу векторының
үнемі траекторияның ойыс жағына қарай
бағытталатындығын, нормаль үдеу туралы
берілген осы түсінік, оны айқындай
түседі.
Бір қалыпты айналмалы және бір қалыпты айнымалы айналмалы қозғалыстар. Егер қозғалыс кезінде бұрыштық үдеу ε=0 болса, онда қозғалыс ω=const тұрақты бұрыштық жылдам-дықпен орындалады. Мұндай қозғалысты бір қалыпты айнал-малы қозғалыс деп атаймыз. Осындай қозғалыстың бұрыштық жылдамдығының анықтамасынан мынадай өрнек алынады:
![]() .
.
Егер t0 = 0 болғанда φ = φ0 десек, соңғы теңдіктен мынадай формула шығады:
![]() ,
(2.72)
,
(2.72)
мұндағы бастапқы φ0=0 болып келген жағдайда (2.72) –теңдіктен:
![]() және
және
 .
(2.73)
.
(2.73)
Дененің айналысы кезінде оның бұрыштық үдеуі ε т±рақ-ты болатын болса, онда мұндай айналмалы қозғалысты бір қалыпты айнымалы дейміз.
Бұрыштық үдеу анықтамасынан:
![]() .
.
Бұл теңдікті сәйкес алынған шектерде (t0=0 саналады) интег-ралдау арқылы, мынадай формула аламыз:
 .
(2.74)
.
(2.74)
Бұл формуламен ε=const болған жағдайдағы бұрыштық жылдамдық анықталады. (2.74)-тің екі жағында dt-ға көбейтіп интегралдау арқылы мынадай формула аламыз:
 .
(2.75)
.
(2.75)
7-сұрақ. Нүктенің шеңбер бойымен қозғалысындағы толық үдеуін қорытыңыз.
Шеңбер бойымен қозғалған нүктенің үдеуін екі құраушыға жіктейміз
a
= a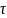 + an
(1)
+ an
(1)
М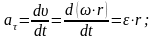 ұнда
жанама үдеудің анықтамасын қолданамыз:
ұнда
жанама үдеудің анықтамасын қолданамыз:
(2)
(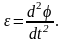
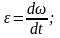 2)
дегі ᶓ шамасын өрнектейтін формуланы
көрсетейік:
2)
дегі ᶓ шамасын өрнектейтін формуланы
көрсетейік:
Немесе (3)
(3) формуламен анықталатын ᶓ шеңбер радиусының айналуының бұрыштық үдеуі д.а. (2) формуланы сөзбен былай айтуға болады:
Шеңбер бойымен қозғалған нүкте үдеуінің жанама құраушысы немесе оның жанама үдеуі бұрыштық үдеу мен радиустың көбейтіндісіне тең болады.
Ү деудің
нормаль құраушысы мынаған тең:
деудің
нормаль құраушысы мынаған тең:
(4)
(2) және (4) формулаларды ескере отырып, толық үдеу векторы a-ны былай жазамыз:
a=ᶓr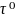 + w²rn⁰
(5)
+ w²rn⁰
(5)
шеңбер боымен қозғалатын нүктенің үдеуінің модулі:
a=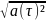 +an²
= r
+an²
= r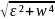 (6)
(6)
толық
үдеу векторы w-нің радиус r мен жасайтын
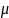 бұрышы мына өрнекпен анықталады:
бұрышы мына өрнекпен анықталады:
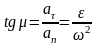

8–сұрақ. Жылдамдықтарды қосу туралы теореманы тұжырымдаңыз және оның қажеттілігін түсіндіріңіз .
Нүкте қозғалысы күрделі қозғалыс деп есептеледі, егер сол нүктенің қозғалысы кемінде екі координаттық жүйелерге қатысты қарастырылса, соңғылардың біреуі «қозғалмайтын» координаттық жүйе болуы қажет.
Нүкте М берілген ![]() координаттар
жүйесінде, ал ол жүйенің өзі басқа бір
«қозғалмайтын»
координаттар
жүйесінде, ал ол жүйенің өзі басқа бір
«қозғалмайтын» ![]() координаттық
жүйесінде қозғалатын болсын. Мұндай
жағдайда нүкте М
жүйсіне
қарағанда күрделі қозғалыста дейміз.
координаттық
жүйесінде қозғалатын болсын. Мұндай
жағдайда нүкте М
жүйсіне
қарағанда күрделі қозғалыста дейміз.
Анықтама. Нүктенің қозғалмалы жүйесіне қатысты қозғалысы оның салыстырмалы қозғалысы деп, жүйесінің негізгі жүйесінде қозғалуын салдарынан болған қозғалысын онын тасымал қозғалысы деп, негізгі жүйесіне қатысты қозғалысы оның абсолют қозғалысы деп атайды.
Нүктенің әрбір қозғалыстағы кинематикалық сипаттамалары сол қозғалыстарға сәйкес аталады.
Жылдамдықтарды қосу туралы
Айталық,
кез келген ![]() уақыт
кезеңіндегі күрделі қозғалыстағы нүкте
кеңістіктің М нүктесінде
болсын (3.1 - сурет).
уақыт
кезеңіндегі күрделі қозғалыстағы нүкте
кеңістіктің М нүктесінде
болсын (3.1 - сурет).
Осы нүктенің абсолют жылдамдығын анықтауын мына теорема мүмкіншілік береді.
Теорема. Күрделі қозғалыстағы нүктенің абсолют жылдамдығы оның салыстырмалы және тасымал жылдамдықтарының геометриялық қосындысына тең.
Дәлелдеу. Шынында, кез келген уақыт кезеңіндегі қозғалушы нүктенің кеңістіктегі орны
 (3.1)
(3.1)
радиус – вектормен анықталады (3.1 - суретті қара).

Бұл
теңдіктің еркін қатты дененің
қозғалысындағы сәйкес теңдіктен
айырлымашылығы мұнда ![]() -
радиус–векторы қозғалыс кезінде бағыты
мен қоса шамасын да өзгертеді.
-
радиус–векторы қозғалыс кезінде бағыты
мен қоса шамасын да өзгертеді.
Қозғалмайтын деп есептейтің жүйесіне қатысты М нүктесінің қозғалысы әдеттегі тұрақты кеңістіктегі нүктенің қарапайым қозғалысы болады. Демек радиус-векторынын «қозғалмайтын» жүйесіне қатысты өзгеруі М нүктенің салыстырмалы қозғалысын сипаттайды, яғни нүктенің салыстырмалы жылдамдығы
![]() ,
(3.2)
,
(3.2)
болады.
Мұнда ![]() -
бірлік векторлар, әрине (3.2)
шамасы
-
бірлік векторлар, әрине (3.2)
шамасы ![]() радиус-векторының,
қозғалыс кезіндегі толық өзгеруі емес,
өйткені
радиус-векторы
жүйесінің О нүктесін
айнала қозғалуынан да өзгереді.
радиус-векторының,
қозғалыс кезіндегі толық өзгеруі емес,
өйткені
радиус-векторы
жүйесінің О нүктесін
айнала қозғалуынан да өзгереді.
Сондықтан, М нүктенің салыстырмалы қозғалысының жылдамдығы радиус-векторының уақыт бойынша жүйесіне қатысты локальдык немесесалыстырмалы туындысы деп аталады:
 (3.3)
(3.3)
(3.1) векторлық теңдеудің екі жағынан да уақыт бойынша туынды алайық:
 (3.4)
(3.4)
мұнда ![]() М нүктесінің
абсолют жылдамдығы;
М нүктесінің
абсолют жылдамдығы;  - О нүктесінің
жылдамдығы.
- О нүктесінің
жылдамдығы.
Бурдың формуласы бойынша
 (3.5)
(3.5)
Мұнда  -
локальдық туынды М нүктесінің
салыстырмалы жылдамдығы болып табылады.
-
локальдық туынды М нүктесінің
салыстырмалы жылдамдығы болып табылады.
Сондықтан,
 (3.6)
(3.6)
Бірақ, ![]() - М
нүктесінің тасымал жылдамдығы
болғандықтан, соңғы теңдікті былай жаза
аламыз:
- М
нүктесінің тасымал жылдамдығы
болғандықтан, соңғы теңдікті былай жаза
аламыз:
 . (3.7)
. (3.7)
Сонымен теорема дәлелденді.
Абсолют жылдамдығының модулі проекциялар әдісі арқылы санақ жүйесі өстеріне проекциялау керек:
![]() (3.8)
(3.8)
және
![]() .
.
9-сұрақ. Қатты дененің ілгерілемелі қозғалысын түсіндіріңіз және оған мысал келтіріңіз.
Дене қозғалысы кезінде онда алынған кез келген кесінді өзіне-өзі параллель көшсе, мұндай қозғалыс ілгерілемелі қозғалыс деп аталады ( сурет). Мысалы: велосипед педаліның қозғалысы, түзу участкіде жылжып бара жатқан автомобиль бортының қозғалысы ілгерілемелі қозғалыстан тұрады. Жалпы ілгерілемелі қозғалыстағы дене нүктесінің траекториясы қисық сызықтан тұрады. Дене ілгерілемелі қозғалысының ерекшелігін төмендегі теоремамен беру мүмкін.

Теорема: Ілгерілемелі қозғалыстағы дененің нүктелері бірдей траекториямен қозғалып, олардың әр кездегі жылдамдықтары және үдеулері бірдей болады.
Дәлелдеу: Дене Oxyz
жылжымайтын
Декарт координаттар жүйесіне қатысты
ілгерілемелі қозғалыста болсын (сурет).
Абсолют қатты дене және ілгерілемелі
қозғалыс анықтамасына сәйкес дененің
кезкелген С нүктесінен М нүктесіне
қарай бағытталған вектор![]() тұрақты
және де
тұрақты
және де ![]() болады
(сурет).
болады
(сурет).
Нәтижеде С нүкте
қандай траектория сызса, ![]() үстіндегі
нүктелерде осындай траектория сызады.
С және М нүктелердің
радиус-векторларын сәйкесінше
үстіндегі
нүктелерде осындай траектория сызады.
С және М нүктелердің
радиус-векторларын сәйкесінше ![]() десек:
десек:
![]() .
(1)
.
(1)
М нүкте жылдамдығын табу үшін (1) ден уақыт бойынша туынды аламыз:

![]() болғандығы
үшін:
болғандығы
үшін:
 ;
;  немесе
немесе ![]() =
=![]() (2)
(2)
(9.2) ден уақыт бойынша туынды алсақ, үдеу табылады:
 =
= немесе
немесе ![]() =
=![]() (3)
(3)
(2) ілгерілемелі қозғалыстағы дене нүктелерінің жылдамдықтары бірдейлігін, ал (3) үдеулердің бірдейлігін көрсетеді. Сонымен, теорема толық дәлелденді.
Демек, дененің ілгерілемелі қозғалысы, оның кезкелген нүктесінің қозғалысымен анықталады, яғни
 (4)
(4)
Анықталған (4) теңдеуі дененің ілгерілемелі қозғалысы кезіндегі қозғалыс заңын береді.
10. Қатты дененің қозғалмайтын өс төңірегіндегі айналмалы қозғалысына анықтама беріңіз және оны зерттеу әдісін түсіндіріңіз.
Қатты дененiң тұрақты осьтi айнала қозғалысы
Денемен өзгермейтiндей боп бекiтiлген, айналу осi деп аталатын бір ғана түзудiң барлық нүктелерi тыныштық қалпын сақтайтын қозғалысты қатты дененiң сол тұрақты осьтi айнала қозғалысы дейдi.

2.3-сурет 2.4-сурет
Берiлген
дененiң (2.4-сурет) қозғалмайтын 0А осiнен
айнала қозғалысын зерттеу үшiн қозғалмайтын
 оң координаталар системасын таңдап
алалық. Айналу осiн екi нүктеде, мысалы
О және А нүктелерiнде, бекiтсек болғаны
оның барлық нүктелерi де қозғалмайды.
Тұрақты Оζ осiн осы тузудiң бойымен оның
оң бағытынан қараған бақылаушы дене
айналуын сағат тiлiнiң қозғалысына қарсы
бағытта көретiндей етiп бағыттайық.
оң координаталар системасын таңдап
алалық. Айналу осiн екi нүктеде, мысалы
О және А нүктелерiнде, бекiтсек болғаны
оның барлық нүктелерi де қозғалмайды.
Тұрақты Оζ осiн осы тузудiң бойымен оның
оң бағытынан қараған бақылаушы дене
айналуын сағат тiлiнiң қозғалысына қарсы
бағытта көретiндей етiп бағыттайық.
Сонда Оζ осi дененiң айналу осi болады. Жалпы жағдайда Оζ осiнiң айналу осiмен бiрiгiп келуi шарт емес. Тек бұл жағдайда зерттеу жеңiлденедi.
Айналу
осi арқылы
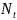 жазықтығын денемен бiрге бекiтейiк.
Бастапқы кезеңде (t=0 болғанда) ол
жазықтықты
жазықтығын денемен бiрге бекiтейiк.
Бастапқы кезеңде (t=0 болғанда) ол
жазықтықты
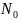 деп белгiлейiк және ол Оζ осi арқылы
өтетiн болсын дейiк. Кез келген t уақыт
өткен соң ол жазықтық денемен бiрге
айнала отырып,
қалпына келедi.
деп белгiлейiк және ол Оζ осi арқылы
өтетiн болсын дейiк. Кез келген t уақыт
өткен соң ол жазықтық денемен бiрге
айнала отырып,
қалпына келедi.
Осы және жазықтықтарының арасындағы екi жақты бұрыш φ қатты дененiң айналу бұрышы деп аталады. Бұл бұрыш берiлген дененiң кез келген уақыт кезеңіндегi кеңiстiктегi орнын бiр мәндi анықтайды, демек, тұрақты осьтi айнала қозғалатын қатты дененің бiр ғана еркiндiк дарежесi болады.
Уақыттың функцясы ретiнде берiлген айналу бұрышы
φ=φ(t)
қатты дененiң айналу заңы немесе айналу теңдеуi деп аталады. Бұл айналушы тұтас қатты дененiң негiзгi кинематикалық характеристикасы болып табылады Дененің бұрыштық жылдамдығы
ω (t) = φ (t)
бұрыштық үдеуi
ε (t) = ω = φ (t)
айналмалы қозғалыстың туынды кинематикалық характеристикалары болады. Бұл шамалар тұтас қатты денеге тән.
Бұрыштық жылдамдықтың болуы айналу осiмен тығыз байланысты болғандықтан оны айналу осiнің бойында жатқан вектор деп қарауға болады. Оның бағытын және айналу осi бойындағы орнын таңдау бiздің өз еркiмiзде, сондықтан да ол сырғымалы вектор болғаны.
Айналу кезiнде қатты дененің барлық нүктелерi жазықтықтары айналу осiне перпендикуляр ал центрлерi айналу осiнде жататын шеңберлер сызады. Нүктенiң шеңбер бойымен қозғалысының кинематикалық характеристикаларын анықтауды бiз жақсы бiлемiз. Айналмалы қозғалыстағы қатты дененің кез келген М нүктесiнің алгебралық жылдамдығы мынадай болады:
v = hφ = hω (2.9)
яғни
дененің бұрыштық жылдамдығы мен нүктенiң
айналу осiнен қашықтығының көбейтiндiсiне
тең өйткенi берiлген М нүктесi үшiн оның
айналу радиусы деп аталатын бұл қашықтық
h = |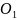 М|
=const, яғни дене абсолют қатты дене. Сонымен
кез келген уақыт кезеңiндегi дене
нүктелерiнің жылдамдықтары олардың
айналу радиустарына тура пропорционал.
Нүкте жылдамдығының бағыты айналу осi
және сол нүкте арқылы өтетiн жазықтыққа
перпендикуляр,
М|
=const, яғни дене абсолют қатты дене. Сонымен
кез келген уақыт кезеңiндегi дене
нүктелерiнің жылдамдықтары олардың
айналу радиустарына тура пропорционал.
Нүкте жылдамдығының бағыты айналу осi
және сол нүкте арқылы өтетiн жазықтыққа
перпендикуляр,
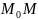 шеңберiне жанаманың бойымен дененің
айналу бағытына қарай бағытталады Олай
болса М нүктесiнiң жылдамдқ векторы v
дененiң ω бұрыштық жылдамдық векторына
және нүктенің r =OМ радиус-векторына
перпендикуляр болады, ал (2.9) өрнегiмен
анықталатын оның шамасы
шеңберiне жанаманың бойымен дененің
айналу бағытына қарай бағытталады Олай
болса М нүктесiнiң жылдамдқ векторы v
дененiң ω бұрыштық жылдамдық векторына
және нүктенің r =OМ радиус-векторына
перпендикуляр болады, ал (2.9) өрнегiмен
анықталатын оның шамасы
v = ω r sin α (2.10)
Мұнда α бұрышы —ω және r векторларының арасындағы бұрыш, яғни
α=(ω, r ). Бұрыштық жылдамдық векторының оң бағытын түрлiше етiп таңдап алу қозғалыстың кинематикалық характеристикаларын өзгертпейдi. Бiрак бiр таңдап алынған бағыт барлық есептеулерде сақталуы қажет. Әдетте бұл бағыт оң винт ережесi бойынша, яғни Оζ осiъмен бағыттас етiлiп алынады. Сонымен бұрыштық жылдамдық векторын айналу осiнiң бойымен кез келген орынға жылжытуға болады.
Бұрыштық жылдамдық уақыт етуiмен байланысты тек шамасын ғана өзгертетiн болғандықтан бұрыштық үдеу векторы ε да айналу осiнiң бойында орналасады. Мұны аналитикалық жолмен де дәлелдеуте болады Бұрыштық жылдамдық векторын былай жазайық:
ω
= ω*
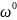 (2.11)
(2.11)
Айналу осі қозғалмайтын болғандықтан оның бірлік векторы тұрақты, яғни
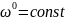
Сондықтан (2.11) теңдігінің екі жағынан да уақыт бойынша туынды аламыз:
ε = ε
Егер ε > 0 болса, онда айналу үдемелi, яғни ω және ε векторлары бағыттас болғанын, ал ε < 0 болса, айналу кемiмелi болады да, ω және ε векторлары бiр-бiрiне қарама—карсы бағытталады.
Жоғарыда М нүктесiнiц жылдамдығының шамасы (2.10) және бағыты туралы айтылғандарды ескерсек,
M = ω x r (2.12)
екенiн көру қиын емес. Бұл формула Эйлер формуласы деп аталып, айналмалы қозғалыстары қатты дененiң кез келген нүктесi үшiн орындалады. Денемен бiрге айналатын кез келген Охуz қозғалмалы координаталар системасы осьтерiнiң бiрлiк векторлары үшiн жааылған бұл формула
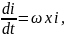

 (2.12`)
(2.12`)
Пуассон формулалары деп аталады.
Эйлер формуласын мына түрде басқаша жазсақ:
M = MO X ω
онда айналмалы қозғалыстағы қатты дененiң кез келген нүктесiнiң жылдамдығы дененiң бұрыштық жылдамдығының сол нүкте арқылы алынған моментiне тең болады.
Жалпы жағдайда жылдамдык векторының қозғалмайтын координаталар осьтерiне проекциялары төмендегiдей болады:
 ,
,
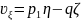 ,
,
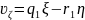 .
.
Қозғалмалы координаталар системасында
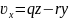 ,
,
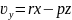 ,
,
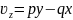
болады.
Мұндағы
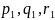 бұрыштық жылдамдық векторының
қозғалмайтын,ал p, q, r - қозғалмалы
кординаталар осьтеріне проекциялары.
бұрыштық жылдамдық векторының
қозғалмайтын,ал p, q, r - қозғалмалы
кординаталар осьтеріне проекциялары.
Жеке
жағдайда Оζ
айналу осі болса,онда
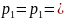 0,
0,
 ω
болады
да
ω
болады
да
 =
0
=
0
Бұл тендiктерде ζ = η = 0 десек, онда айналу осiнде жатқан нүктлердiң қозғалмайтынын көремiз.
Дене нүктелерiнiң үдеулерiн табу үшiн (2.12) өрнегiнен уақыт бойынша туынды алып, r= ωекiнiн ескерсек, онда М нүктесiнiң үдеуi
W = ε X r + ω X r (2.13)
болады.
Оң
бұрғы ережесi бойынша бұл теңдiктiң оң
жағындағы қосылғыштардың бiрiншiсi
нүктенiң жылдамдық векторымен бағыттас,
екiншiсi М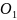 түзуiнің бойымен
центріне қарай айналу осiне перпендикуляр
бағытталады (сондықтан ол оське тартқыш
үдеу делiнедi).
түзуiнің бойымен
центріне қарай айналу осiне перпендикуляр
бағытталады (сондықтан ол оське тартқыш
үдеу делiнедi).
