6.Формула Бейеса.

Формула Бейеса используется для оценки (переоценки) уже произошедшего события (его гипотез).

Теорема гипотез (Бейеса): Пусть события В_i образуют полную группу событий. Тогда условная вероятность события В_i при условии, что событие А произошло вычисляется по формуле:

.

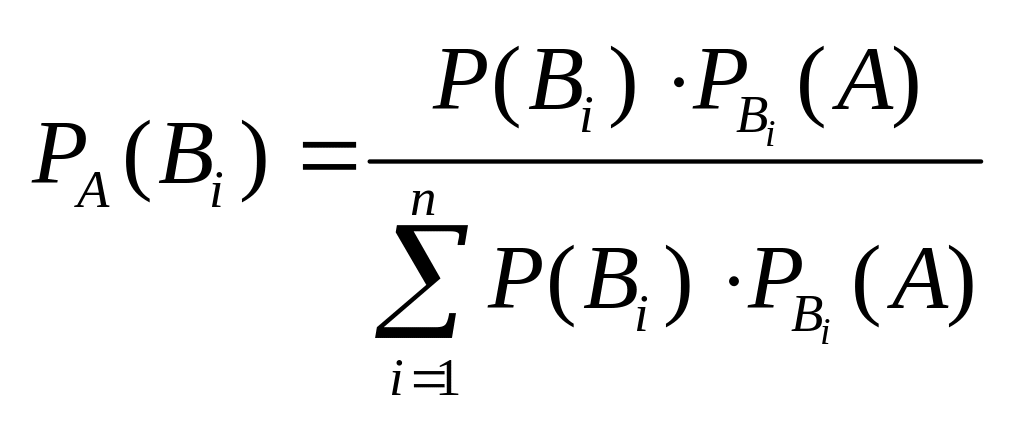Д-во: Согласно определению условной вероятности: 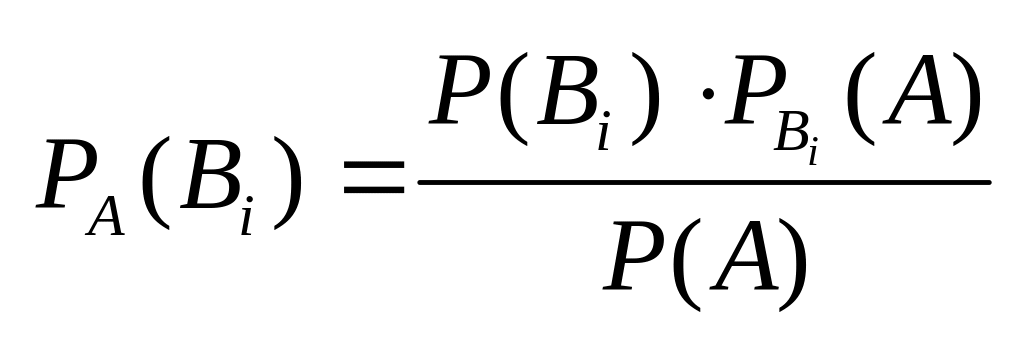, , где Т.Д.

Пр.: 2 ящика подвергаются проверке на стандартность. Вероятность этого для 1-го ящика – 0,3, для 2-го – 0,7. Вероятность того, что болт будет признан стандартным из 1-го ящика – 0,96, из 2-го – 0,82. Болт оказался стандартным. Найти вероятность того, что этот болт из 1-го ящика. Реш.: Пусть А– болт стандартный, В1– 1-ый ящик проверяют, В2– 2-ой ящик проверяют, Р(В₁)=0,3, Р(В₂)=0,7, Р_В1(А)=0,96, Р_В2(А)=0,82, Р_А(В₁)= Р(В₁) ·Р_В1(А)/( Р(В₁) ·Р_В1(А)+ Р(В₂) ·Р_В2(А))=0,3·0,96/(0,3·0,96+0,7·0,82)=0,334.

7.Интегральная функция распределения вероятности и её свойства.

Ф-цией распределения (интегральной ф-цией) наз. ф-ция F(х), определяющая вероятность того, что СВ Х в результате испытаний примет значение меньше х, F(х)=P(X<x).

Свойства:

1. , т.е. F(x)– ограничена. Д-во следует из определения интегральной ф-ции.

2.F(x)-функция неубывающая, х₁<х₂, следовательно . Д-во: т.к. х₁<х₂, найдем , , следовательно -большему значению аргумента соответствует большее значение функции.

Следствие1: Вероятность того, что СВ Х примет значение в интервале (a,b) равна приращению ф-ции на этом интервале:

Следствие2: Вероятность того, что непрерывная СВ Х примет одно определенное значение равна 0.

3. , если на (a,b) и F(x)=1, если на (a,b). Д-во: Если возможное значение СВ принадлежит (a,b), то F(x)=0, при ,т.к. это событие невозможное (вероятность невозможного события равна 0). F(x)=1,при .т.к. это событие достоверное (вероятность достоверного события равна 1)

Пр.: Дискретная СВ задана таблицей:

xi	2	2	5
pi	0,1	0,7	0,2

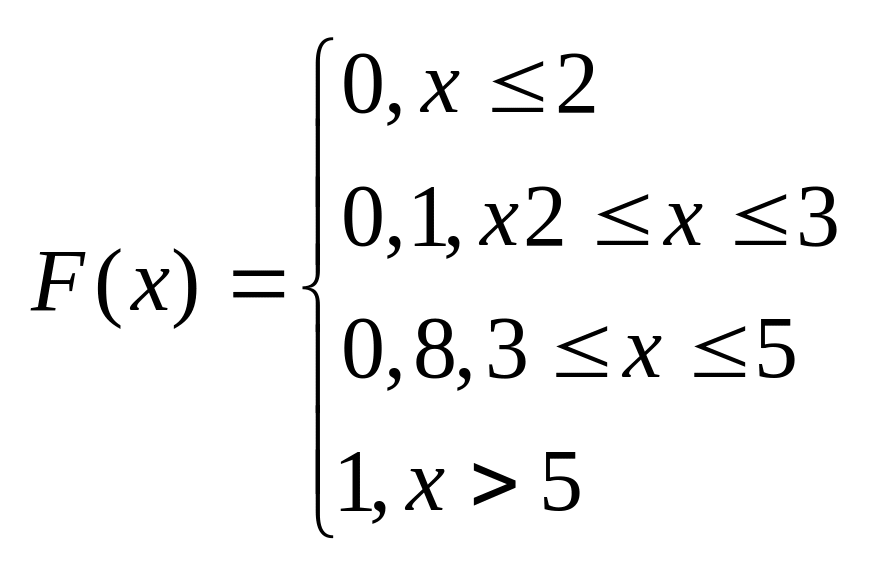
8.Плотность распределения вероятностей и её свойства.

Плотностью распределения (сущ. только для непрерывных СВ) наз. первая производная от ф-ции распределения.

Свойства:

1.Плотность f(x) неотрицательная ф-ция, т.к. ее ф-ция распределения F(x) неотрицательна, след. производная от нее тоже неотрицательна.

2.Несобственный интеграл от плотности распределения в интервале от -∞ до +∞ равен1. . Д-во: Несобственный интеграл равен 1, выражает вероятность события того, что СВ примет значение, принадлежащее интервалу (-∞;∞), такое событие достоверно. Геом. смысл: площадь криволинейной трапеции, кот. ограничена осью 0Х и кривой 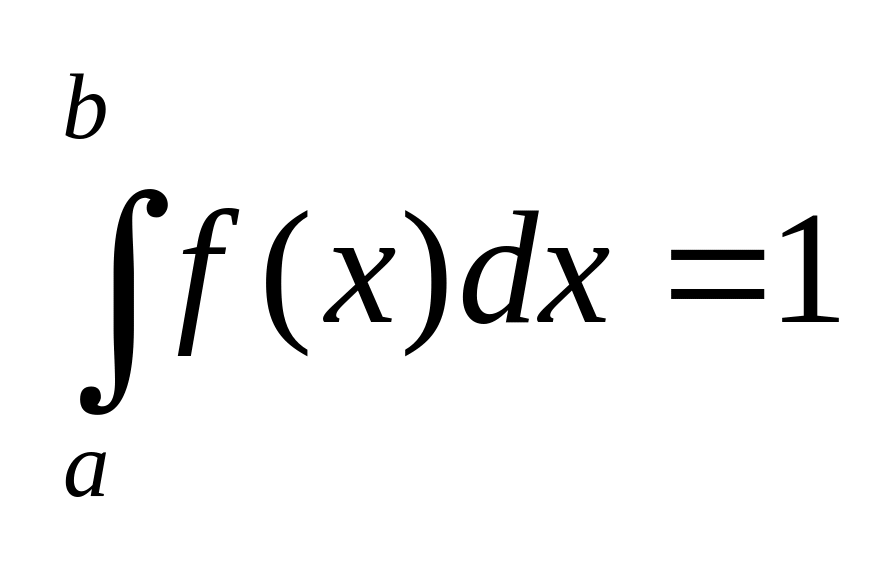равна 1.

Теорема: Вероятность того, что непрерывная СВ примет значение заключенное в (a,b) равна определенному интегралу от плотности распределения в пределах от a до b.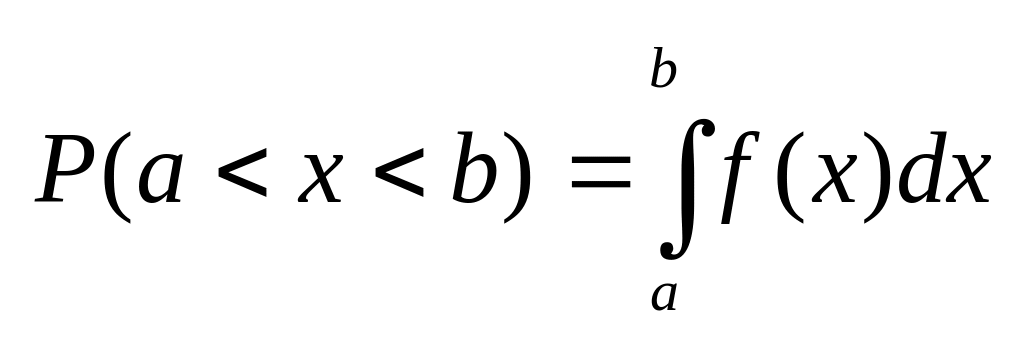 , где

Д-во: Используя свойство ф-ции распределения Р(a<x<b)=F(b)-F(a), по формуле Ньютона-Лейбница Т.Д.

Замечание: Вероятность того, что непрерывная СВ примет значение, заключенное в (a,b) равна площади криволинейной трапеции, кот. Ограничена осью 0Х и кривой f(x) и прямыми x=a и x=b.

Теорема: Если f(x)– плотность распределения некоторой СВ, то

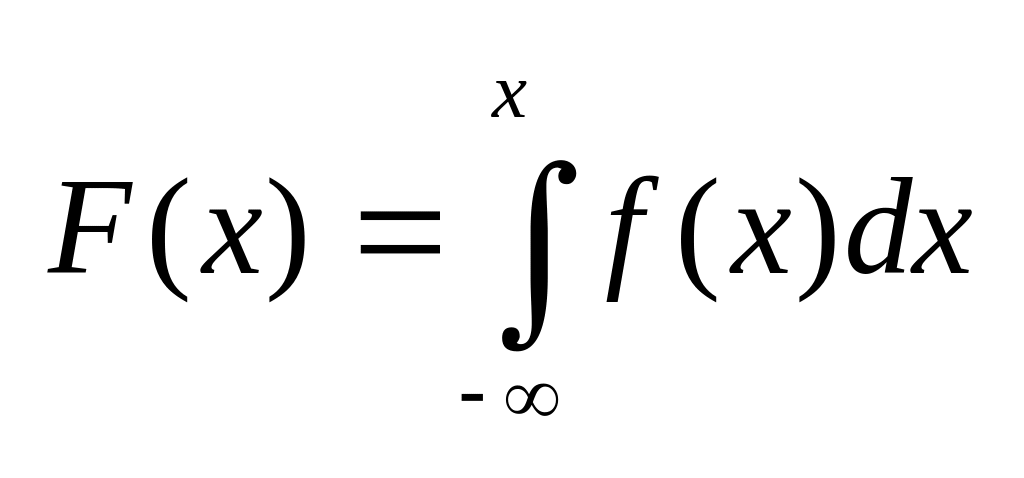
Д-во: . Пусть a=-∞, b=x, тогда .Т.Д.