1.3 Расчет теплового баланса токоведущей шины.

Для единицы длины токопровода уравнение теплового баланса будет иметь вид:

(1.15)

где dQ_l - количество тепла, выделяющееся в единице длины проводника;

dQ₂ - количество тепла, затрачиваемое на нагрев проводника;

dQ₃ - количество тепла, отводимое с боковой поверхности проводника.

Составляющие данного уравнения определяются следующими выражениями:

(1.16)

(1.17)

(1.18)

где в представленных выражениях:

I - величина токовой нагрузки проводника;

к_д - коэффициент дополнительных потерь;

ϑ - температура проводника;

ϑ₀ - температура окружающей среды;

q - поперечное сечение проводника;

Физические параметры материала проводника:

ρ_о - удельное электрическое сопротивление при 0 °С;

α - температурный коэффициент сопротивления;

с - удельная теплоемкость;

γ- плотность материала;

r_ТΣ - суммарное тепловое сопротивление между поверхностью проводника и окружающей средой на единицу длины.

Таким образом, уравнение теплового баланса будет иметь следующий вид:

(1.19)

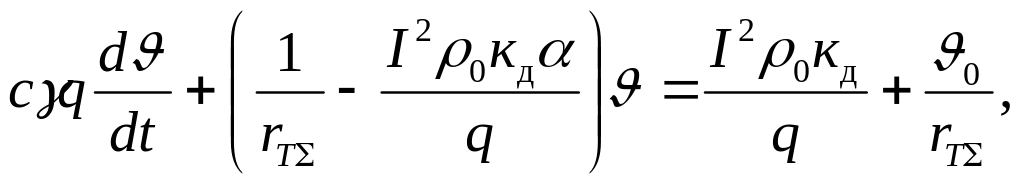(1.20)

Так как у нас продолжительный режим и температура не меняется со временем, получаем:

(1.21)

Сначала определим коэффициент дополнительных потерь соответственно

(1.22)

где К_ПЭ - коэффициент поверхностного эффекта;

К_Б- коэффициент близости.

Откуда видно, что коэффициент поверхностного эффекта это функция которая отвечает

(1.23)

где ψ - сама функция;

ƒ - частота, равная = 50 (Гц); [ 8 ]

R₁₀₀ - тепловое сопротивление для 100м.

Рассчитаем для нашего токопровода, т.е.

(1.24)

где ρ₀=10·10^-8(Ом·м) - удельное электрическое сопротивление. Для стали:

- температурный коэффициент сопротивления.

Поперечное сечение равно

Согласно к формуле (1.24)

Соответственно формуле (1.23)

Рисунок 1.3 - Зависимость коэффициента поверхностного эффекта для трубчатых проводников из немагнитного материала с разными соотношениями δ/d от параметра , где δ - толщина стенки трубы, м; ƒ - частота переменного тока, Гц; R₁₀₀- активное сопротивление постоянного тока трубчатого проводника длиной

[ 9 ]

Значение К_ПЭ определяем по графику (рис. 1.3)

,

Тогда коэффициент дополнительных потерь по уравнению (1.22)

Из уравнения (1.20) выразим площадь поперечного сечения q:

(1.25)

Исходя из этого, можем рассчитать действительное значение диаметра шинопровода:

(1.26)

Рассчитаем плотность тока по указанной формуле

(1.27)

.

2. Проверочный тепловой расчет токопровода

1. Окончательное определение источников тепла в токопроводе и расчет их суммарной тепловой мощности с учетом дополнительных потерь и потерь в не токопроводящих элементах.

Рабочую температуру шины примем равной допустимой температуре нагрева.

Определим тепловую мощность слоя воздуха между токоведущей шиной и стальной оболочкой

(2.1)

где ϑ_доп, ϑ₁ - допустимая температура токоведущей шины и внутренняя температура оболочки соответственно;

R_Т1 - тепловое сопротивление воздушной прослойки.

Итак:

Определим тепловую мощность для оболочки

(2.2)

Суммарная тепловая мощность определяется по формуле:

(2.3)

Соответственно, к формуле (2.3)