Експертиза економетричної моделі

Після визначення рівняння регресії доцільно провести оцінку адекватності отриманої залежності та достовірності результатів.

Для цього можна використати величину коефіцієнта де­термінації R². Достатньо близьке до 1 значення R² підтверджує, що варіація результуючої змінної значною мірою визначається варіацією факторних змінних. Чим більше вибіркові значення наближаються до лінії регресії, тим більше коефіцієнт детермінації наближається до 1.

Для оцінювання статистичної значущості коефіцєнта детермінації, як правило, застосовують критерій Фішера. Для цього можна використати величини F і df у вихідних даних функції LINEST та знайти ймовірності отримання найбільшого значення F, порівнюючи величину F з критичними значеннями в опублікованих таблицях F-розподілу.

Для перевірки невипадковості високого значення R2 застосовується також стандартна функція FDIST. Для цього необхідно задати параметри функції таким чином:

FDIST(x, Deg_freedom1, Deg_freedom2 ),

де x – розрахункове значення F–статистики;

Deg_freedom1 – кількість незалежних змінних у рівнянні регресії;

Deg_freedom2 – розраховане число ступенів свободи.

Дана функція повертає значення , яке показує імовірність помилкового висновку щодо сильного впливу незалежних змінних на результуючу, відповідно (1-) – імовірність того, що такий вплив існує.

Оцінка достовірності значень коефіцієнтів рівняння регресії здійснюється з використанням стандартної функції TDIST, яка має такий синтаксис:

TDIST(x, Deg_freedom, Tails),

де x – – фактичні значення статистик для і-го коефіцієнта в рівнянні регресії;

Deg_freedom – число ступенів свободи;

Tails – 1 (ознака використання одностепеневого розподілу Стьюдента).

Функція TDIST повертає значення , яке є ймовірністю того, що значення i-го коефіцієнта в рівнянні регресії є недостовірним. Відповідно величина 1- є ймовірністю того, що значення i-го коефіцієнта достовірне.

Виходячи з результатів 2–4 етапів моделювання, дослідник приймає рішення про адекватність моделі та форму зв'язку між показни­ками. З певною мірою довіри обрана модель може використовуватись для прогнозування значень залежного показника.

Приклад побудови рівняння лінійної регресії в середовищі ms excel

Розглянемо приклад побудови рівняння лінійної регресії на основі статистичних даних, наведених у додатку. Допускаючи, що існує залежність величини валового регіонального продукту від прямих іноземних інвестицій в регіони, проілюструємо етапи побудови економетричної моделі на основі цих даних в середовищі MS Excel. Для даного прикладу приймемо такі позначення:

x – прямі іноземні інвестиції в регіони (факторна змінна);

у – валовий регіональний продукт (результуюча змінна).

На робочому аркуші електронної таблиці MS Excel побудуємо табли­цю вхідної інформації, як показано на рис.1 (блок клітинок A1:D28), де в діапа­зоні клітинок D2:D28 – значення змінної х; а в діапазоні С2:С28 – значення змінної у.

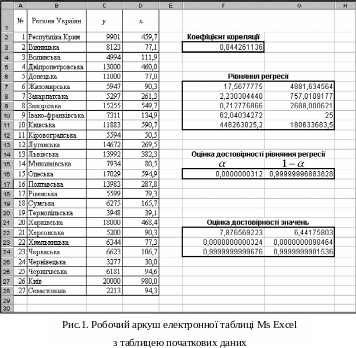
Д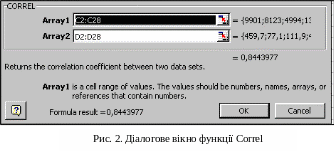 ля того, щоб визначити тісноту зв'язку між змінними x та y, обчислимо коефіцієнт кореляції за допомогою стандартної функції CORREL. Для цього необхідно:

1. Активізувати деяку клітинку, на рис.2 – це F3;

2. За допомогою команди InsertFunction або шляхом натиснення на кноп­­ку f_x на стандартній панелі інструментів викликати стандартну функцію Correl.

3. Ввести параметри функції, як показано на рис. 2.

Функція повертає значення: 0,8443977 >0,7 , отже, існує тісний зв'язок між змінними та є сенс будувати модель.

Припустивши, що лінійна залежність досить добре апроксимує емпіричні дані, побудуємо лінійне рівнняння регресії. Для цього необхідно:

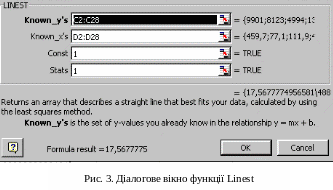
1. Виділити деякий блок клітинок, на рис.2 – це блок F7:G11, в якому рядків – 5, а стовпців – n+1=1+1=2, де n – кількість факторних змінних.

2. З а допомогою команди InsertFunction або шляхом натиснення на кноп­ку f_x на стандартній панелі інструментів викликати стандартну функцію Linest. У діалоговому вікні функції Linest ввести параметри функції, як показано на рис.3.

3. Натиснути на комбінацію клавіш: <Shift> <Ctrl> <Enter>.

У результаті цих дій блок клітинок F7:G11 буде заповнено результатами обчислень:

17,5677775	4881,634564
2,230384448	757,8109177
0,712776866	2688,000621
62,04034272	25
448263025,2	180633683,5

Рядки цього блоку містять:

• перший рядок – коефіцієнти рівняння регресії:

a₁ = 17,5677774956581; a₀ = 4881,63456387435;

• другий рядок – стандартні похибки оцінок параметрів моделі: 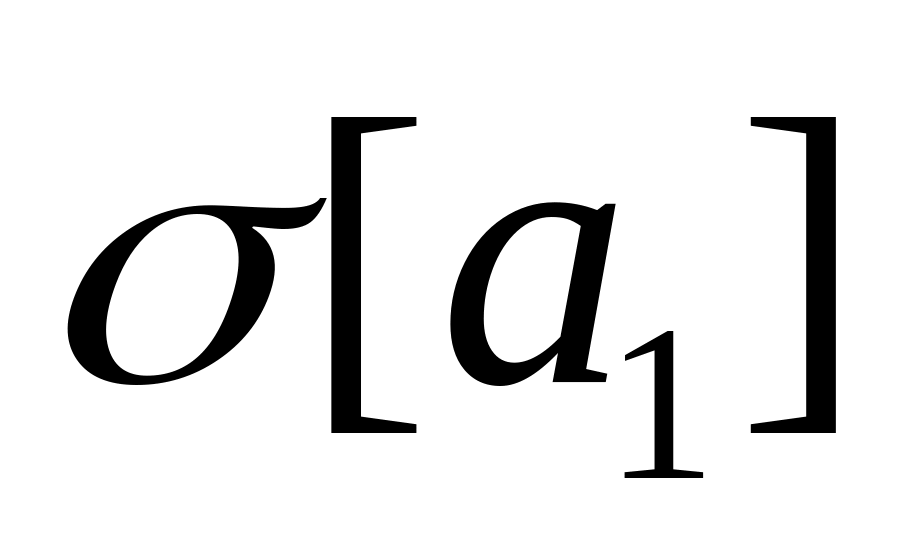=2,23038444766962; =757,810917655815;

• третій рядок – коефіцієнт детер­мінації =0,712776866243426 та серед­ньо-квадратичне відхилення цього показника 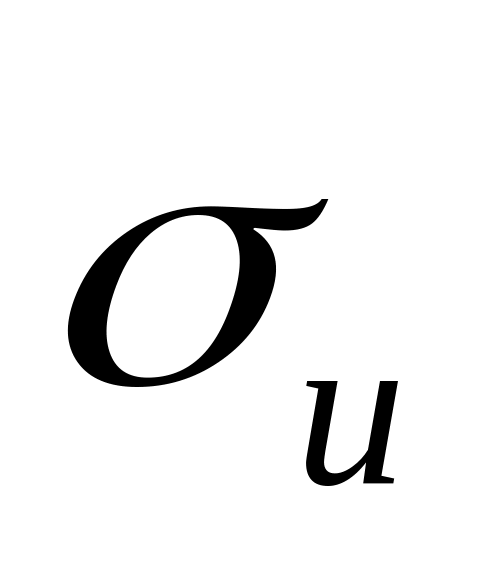=2688,0006212329;

• четвертий рядок: у першій клітинці – розрахункове значення F–статистики F_розр, =62,0403427224907, а у другій клітинці – число ступенів свободи df =25;

• п’ятий рядок: в першій клітинці – сума квадратів відхилень розрахункових зна­чень результуючої змінної від їхнього середнього значення ( =448263025,24703), а в другій клітинці – сума квадратів залишків ( 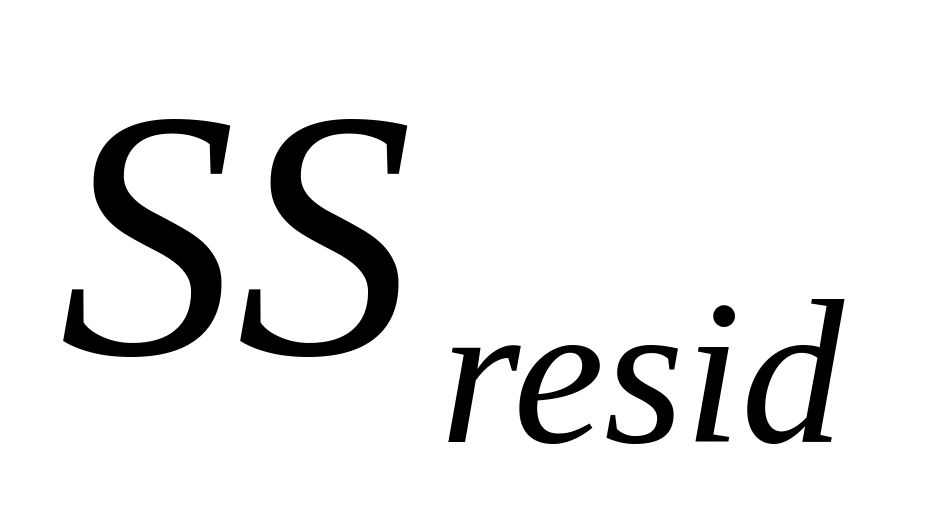=180633683,493711).

Проаналізувавши отримані значення, можна зробити висновок, що

1. Рівняння регресії має вигляд:

.

2. Значення коефіцієнта детермінації , яке міститься в клітинці F9, досить високе і дорівнює 0,712776866, отже, регресійна функція досить добре апроксимує емпіричні дані.

Проілюструємо наступний етап моделювання – оцінку адекватності моделі експериментальним даним. Для цього можна використати стандартну функцію FDIST таким чином:

1. Курсор помістити в деяку клітинку – F16.

2. Викликати функцію FDIST.

3. У діалоговому вікні функції FDIST ввести параметри (рис. 4).

4. Ввести в клітинку G16 формулу: = 1- F16.

Отримане в клітинці G16 значення 0,99999996883828 показує імовірність того, що коефіцієнт детермінації є статистично значущим, отже, факторна змінна x достатньо пояснює стохастичну залежність показника y.

Д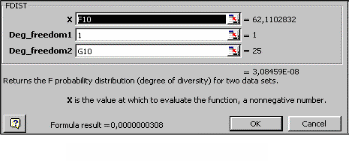 ля оцінки достовірності значень коефіцієнтів регресії використаємо стандартну функцію TDIST.

Для цього визначаємо фактичні значення статистик для коефіцієнтів рівняння регресії :

1. Вводимо формулу у клітинку F22: = F7/F8.

2. Копіюємо дану формулу в клітинку G22: = G7/G8.

В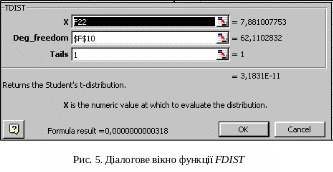 изначаємо імовірність  того, що коефіцієнти рівняння регресії недостовірні. Фіксуємо курсор в клітинці F23 та викликаємо стандартну функцію TDIST: На екрані з'явиться діалогове вікно функції, в якому необхідно ввести параметри, як показано на рис. 5:

В якості параметра Ded_freedon (число ступенів свободи – df) використовується значення, яке міститься в блоці результатів функції LINEST (клітинка $F$10).

Параметр Tabs набуває значення 1, що означає: використовується одностепеневе розподілення Стюдента.

Функція TDIST повертає значення: 0,0000000000324.

Копіюємо формулу, введену в клітинку F23, у клітинку G23: =TDIST(G22;$F$10;1). У клітинці G23 отримано значення: 0,0000000098464.

Визначаємо (1-) – ймовірність того, що значення a_i достовірні:

1. У клітинку F24 вводимо формулу: = 1- F23.

2. Копіюємо дану формулу в клітинку G24: = 1- G23.

У результаті в клітинці F24 отримано значення: 0,9999999999682; в клітинці G24 – значення: 0,9999999903354.

Отже, можна стверджувати що коефіцієнти рівняння регресії достовірні.

Таким чином, побудована модель з високим ступенем надійності адекватна еспериментальним даним і може бути використана для прогнозних оцінок регіонального валового продукту. Формули, застосовані для розрахунків, наведені в електронній таблиці на рис. 6.