ПРИМЕР.
Расставить пределы интегрирования в сферической системе координат.
,
где
- ограниченная поверхность.
;
,
т.к.
.
;
.
§ .. Геометрические и механические приложения кратных интегралов.
Мера множества (площадь, объем).
Пусть
,
- измеримое
(доказательство смотри раньше, приняв
):
при n=2
;
при n=3
.
Для определенного интеграла:
а) Пусть - каноническая область I-го типа (смотри ранее).
.
Аналогично для - каноническая область II-го типа:
.
б
)
Пусть
- криволинейный сектор
.
Тогда:
.
Если область охватывает начало координат:
.
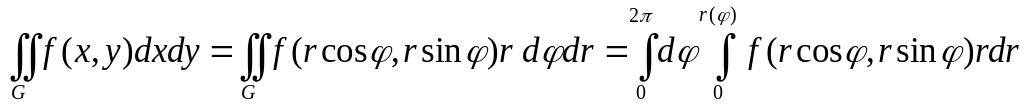б’) Объем цилиндрического тела.
и однозначна.
в) Если
и имеет непрерывные частные производные
в области
,
то
:
1)
,
где
- проекция на
плоскость XOY.
2)
:
,
-
проекция на плоскость XOZ.
3)
:
,
- проекция на плоскость YOZ.
4)
Случай
неявного задания поверхности:
.
Площадь
,
заданной уравнением
выражается интегралом:
5) Случай параметрического задания поверхности.
Если уравнение поверхности задано параметрически:
,
где
,
- ограниченная область, в которой функции
непрерывно-дифференцируемы, то:
где
и
.
ЗАМЕЧАНИЕ.
Площадь поверхности в полярных координатах:
.
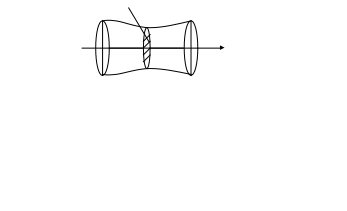
6)
Пусть
- тело с заданной площадью поперечного
сечения.
.
7
)
Пусть
- тело, полученное вращением криволинейной
трапеции вокруг оси OX.
.
Из 6
следует, что
.
8) Объем - цилиндроида (см. ранее).
.
Механические приложения.
Масса пластинки (тела).
Пусть
.
В
определена функция
- плотность (поверхностная или объемная),
т.е.
- материальное тело.
●
Пусть
:
- масса
.
Положим по df:
.
Тогда:
,
n=2
-
пластинка.
,
n=3
– тело.