3. Привидение системы к астатизму

Система статическая, т.к. коэффициент астатизма равен нулю, значит, в системе будет статистическая ошибка. Что бы избежать этого, необходимо в систему поставить регулятор. Целесообразно поставить пропорционально – интегральный - дифференциальный регулятор (ПИД - регулятор).

Передаточная функция ПИД – регулятора[2]:

(5.6)

где: T₁²=k_д/k_и – первая постоянная времени регулятора,

Т₂= k_п/k_и – вторая постоянная времени регулятора,

k_п - коэффициент усиления пропорционального канала регулятора,

k_и - коэффициент усиления интегрального канала регулятора.

k_д - коэффициент усиления дифференциального канала регулятора.

Система становится астатической и статистическая ошибка с ПИД – регулятором равна нулю.

ПИД – регулятор обладает свойствами форсирующего звена второго порядка. При управлении от ПИД – регулятора колебательным объектом второго порядка регулятор может компенсировать колебательные свойства объекта управления и обеспечить плавные апериодические процессы в системе.

Логарифмическая характеристика системы представлена на чертеже

КР-2068.998-26-03-00.00.000.Д лист 1.

После добавления в систему данного регулятора, передаточная функция замкнутой системы будет выглядеть следующим образом:

Ф(p)=(5.7)

4. Исследование влияния параметров на устойчивость системы.

Исследование проводится методом D – разбиений, и область устойчивости строится в плоскости двух задаваемых параметров системы: постоянная времени объекта управления T_о и коэффициент усиления объекта k_о. Для выполнения исследования необходимо найти характеристический комплекс системы. Для этой цели характеристический полином системы (5.8) преобразуется таким образом, что вместо числовых значений исследуемых параметров в него бы вошли их буквенные обозначения (5.9):

С(p) = (T_оp+1)p + k_о·k_им·k_д· k_р (5.8)

C(p) = (T_оp+1)p + k_о·31,6 (5.9)

Преобразуем характеристический полином в характеристический комплекс подстановкой p=jω [1]:

G(jω) = (T_оjω+1) jω + k_о·31,6 (5.10)

Запишем условия для граничной устойчивости системы:

(5.11)

Решив систему уравнений граничной устойчивости найдем параметрические уравнения границы области устойчивости.

(5.12)

При ω=0: K=0, T=∞

Используем условия устойчивости:

с₀=0 и с₂=0, что дает T_о=0 и k_о=0.

Область устойчивости в соответствии с полученными выражениями показана на рис.9.

Рис. 9. Область устойчивости

Область допустимых значений - K_o > 0 и T_o > 0.

Правило штриховки. Для его применения найдем определитель[1]:

(12.1)

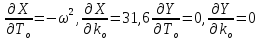(12.2)

Таким образом,

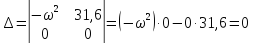
Следовательно, определитель положителен для положительных частот и штриховка должна вестись от кривой при движении по ней в сторону возрастания частот.

Для проверки построений на графике нанесем точку (k_о,Т_о) (зависящие от ω). Примем точку А с координатами (0,13;0,54), принадлежащую данной области устойчивости. Подставим координаты в выражение характеристического полинома и проверим на устойчивость по критерию Гурвица.

G(p) = 10p² + p + 5,6

Первое условие: с₀ = 10> 0; с₁ = 1> 0; c₂ = 5,6 > 0;

Второе условие:

∆ = = с₁·с₂-(с₃·с₀) =5,6·1-10·0= 5,6> 0.

Критерий устойчивости Гурвица подтверждает устойчивость полученной системы с выбранной точкой А, точка попадает в построенную область устойчивости, следовательно область устойчивости построена верно.