
ОТУ2
.doc|
1. Принципы регулирования. 1. Принцип отклонения регулируемых величин от заданного значения (принцип отклонения). 2. Принцип регулирования по возмущению (по нагрузке). 3. Принцип комбинированного управления. В качестве примера системы, работающей по принципу отклонения рассмотрим систему стабилизации скорости вращения двигателя постоянного тока, упрощенная принципиальная схема которого имеет вид (рис1), где ЭУ – электронный усилитель, Д – двигатель постоянного тока (ротор), ОВД – обмотка возбуждения двигателя, ω – угловая скорость двигателя, ТГ – тахогенератор (эл. машина, сигнал на выходе которой пропорционален угловой скорости (рис2) Uтг=kтгω, kтг=tgα – коэффициент), ОВТГ – обмотка возбуждения тахогенератора, МН – момент нагрузки на валу двигателя, ПЗ – потенциометр задания (переменный резистор, шкала которого проградуирована в единицах угловой скорости), ∆U – сигнал ошибки, Uз – напряжение задания, с помощью которого задается заданная скорость вращения двигателя. Механическая характеристика двигателя (рис3). От системы стабилизации требуется, чтобы ω=const при изменении МН. Система может работать в 2-х режимах: 1. Режим задания угловой скорости с помощью ПЗ, устанавливающего заданную скорость вращения. Uз усиливается ЭУ и прикладывается к двигателю, который начинает вращаться и одновременно вращает ТГ, на выходе которого появляется напряжение Uтг. Два источника напряжения Uтг и Uз соединены встречно, в результате чего сигнал ∆U=Uз-Uтг, Uтг≈Uз, ∆U≈0. Устанавливается заданная скорость вращения. ТГ выполняет роль отрицательной обратной связи и служит для формирования сигнала ошибки ∆U. Графически этот процесс изменения во времени можно представить в виде (рис4). Т. к. двигатель обладает инерционностью и мгновенно разогнаться не может, то разгон происходит постепенно и в точке 1 Uтг≈Uз, ∆U≈0. В результате чего Uтг>Uз и возникает ошибка другого знака. При этом усилитель уменьшает напряжение, прикладываемое к двигателю, обороты уменьшаются, спустя некоторое время устанавливается заданная скорость вращения ω=ω(t). Зависимость называется кривой переходного процесса, по которой судят о качестве функционирования системы. Математически это есть решение дифф. уравнения, связывающего переменные Uз и ω. Поэтому, чтобы получить это решение, необходимо для каждого элемента системы управления составить мат. модели и, исключая промежуточные переменные, найти связь м/у Uз и ω. 2. Режим стабилизации при изменении нагрузки на валу двигателя, например, при ее увеличении обороты двигателя уменьшаются и ошибка системы ∆U увеличивается, а, следовательно, увеличивается напряжение, прикладываемое к двигателю, обороты возрастают. В системе возникают колебания и, спустя некоторое время, ∆U≈0 и обороты вернуться к прежнему значению. Графически (рис5 и рис6). ω=ω(t) называется кривой переходного процесса и представляет собой решение дифф. уравнения, связывающего переменные ω и МН. Практически любую САУ можно представить состоящей из объекта регулирования и регулятора, причем это деление условно, т. е. часть элементов можно отнести к регулятору и наоборот, поэтому рассматриваемую систему в общем случае можно представить в виде (рис7), где g(t) – управляющее воздействие, g(t)=Uз (для нашего примера), x(t) – ошибка системы (сигнал рассогласования), x(t)=∆U (для нашего примера). Регулятор – устройство для выработки регулирующего воздействия z(t), регулятор – усилитель (для нашего примера), z(t)=Uд, f(t) – внешнее возмущающее воздействие, f(t)=МН, y(t) – регулируемая величина, y(t)=ω (для нашего примера). Алгоритм регулирования по принципу отклонения: z(t)=φ(x). Для повышения качества функционирования этот алгоритм усложняют и вводят в закон регулирования производные и интегралы от ошибок, тогда z(t)=φ(x, x|, x||,…, ∫x(t)dt,…). Функциональная схема САУ, работающая по принципу регулирования по возмущению (нагрузке) имеет вид (рис8). При таком способе регулирования изменяется возмущающее воздействие f(t). Преображается в усилительно-преображающем устройстве (УПУ) и вводится внутрь канала регулирования. При этом не формируется сигнал ошибки, что является недостатком этого принципа. Кроме того можно измерять f(t). Поэтому этот принцип получил ограниченное распространение. Наибольшее распространение получил принцип комбинированного управления, который сочетает в себе 2 предыдущих принципа, и по которому строятся современные системы управления. |
2. Типовая функциональная схема САУ и назначение основных элементов. На структурных и функциональных схемах сравнение сигналов условно для наглядности изображается в виде (рис1). Эти элементы являются фиктивными и используются лишь для наглядности, т.к. в действительности сравнение сигналов осуществляется на выходах усилителей и специальных схем сравнения сигналов. В общем случае система управления должна состоять из следующих элементов (рис2). 1 – преобразовательный элемент, служащий для преобразования управляющего воздействия φ(t) в вид энергии, необходимый для дальнейшего использования (пример: переменный резистор). 2-5 – элементы сравнения. 3 – модель. 4 – последовательное корректирующее устройство, служащее для придания системе определенных динамических свойств. 6 – усилитель мощности. 8 – исполнительное устройство (различные двигатели, заслонки, электрические магниты и т.д.). 7 – местная отрицательная обратная связь, служит для придания системе определенных динамических свойств. 9 – объект регулирования. 10 – главная отрицательная обратная связь.
|
3. Преобразования Лапласа. При исследовании и проектировании САУ широкое распространение получило преобразование Лапласа, которое позволило заменить дифф. уравнение алгебраическим
P=σ+jω - комплексное число, σ и ω – вещественные числа. Преобразование Лапласа преобразовывает функцию вещественного переменного f(t) в функцию комплексного переменного F(P), называемую изображением функции f(t). F(P)=L {f(t)} 1.Свойства линейности
Пусть система управления описывается линейным неоднородным дифф. уравнением n-порядка
В теории управления дифф. уравнение принято записывать так, чтобы в левой части находилась выходная переменная с своими n-производными, а в правой части входная переменная со своими m-производными. Такая форма записи называется стандартной. Найдем изображение по Лапласу этого дифф. уравнения, для чего умножим левую и правую части на e-pt и проинтегрируем от 0 до ∞
или в сокращенной форме записи
Обычно САУ рассчитывают при нулевых начальных условиях, т.е. последующее воздействие прикладывается к системе после обработки ей предыдущего воздействия, поэтому все члены, зависящие от начальных условий будут равны 0
xвх(p) и xвых(p) – изображения входных и выходных сигналов Уравнение (2) является алгебраическим, из которого можно найти отношение
R(P), Q(P) – многочлены степени P, W(P) – передаточная функция Передаточная функция – отношение преобразования по Лапласу выходной переменной к преобразованию по Лапласу входной переменной при нулевых начальных условиях. Отношение выходного сигнала к входному, если их размерности одинаковы, называется коэффициентом усиления, а если размерности различны, то коэффициентом передачи. После нахождения передаточной функции звена или системы ее математическую модель на структурных схемах представляют в виде (рис1) xвых=W(P)xвх Формально уравнение (2) можно получить из уравнения (1), если последним обозначить
После замены передаточная функция будет равна
Тогда математическая модель (рис2) Пусть система или звено описано дифф. уравнением
Чтобы найти передаточную функцию, заменим
|
4. Составление уравнений пассивных корректирующих устройств. Наибольшее распространение получили пассивные корректирующие устройства в виде четырехполюсника вида (рис1), где Z1(P) и Z2(P) – комплексные сопротивления. Обычно такие четырехполюсники строятся на элементах R, L, C. Для резистора Z(P)=R, для конденсатора Z(P)=1/CP, для индуктивности Z(P)=LP. Найдем передаточную функцию четырехполюсника:
Найдем передаточную функцию и запишем дифф. уравнение корректирующего фильтра вида (рис2)
T=RC, С – постоянная времени фильтра. (рис3) Зная передаточную функцию легко записать дифф. уравнение элемента:
(рис5). Найти передаточную функцию и записать дифф. уравнение корректирующего фильтра (рис6).
Обозначим
|
|
5. Передаточная функция операционного усилителя. Виды операционных усилителей: 1. Масштабные.(рис)
к- коэффициент усиления обратной связи. Т.е. в этом виде усилитель осуществляет матем. Операцию умножеиня на постоянное число. 2. Суммирующие (рис)
UВЫХ=-(K1U1+K2U2+…+KnUn) Kn=R0/Ri i=1…n Обычно коэффициеты к бывают известны, либо изменяются в САУ, поэтому зодавась номиналом коэф-том обр. св. R0=1мОмрассчитываем R 3. Интегрирующие (рис)
4. Интегральный суммирующий (рис)
|
6. Составление уравнения активного корректирующего устройства. Активные коррект. Устр-ва обладают большими возможностямми, чем пассивные. Во многих случаях они строятся на базе усилителей постоянного тока. Схема такого кор устр имеет вид (рис): Z1(p) - комплексное входное сопротивление, Z2(p) – компл сопротивление цепи обратной связи Iвх – входной ток ∆U – сигнал ошибки на входе УПТ (УПТ будем считать идеальным). УПТ с обратной связью работает как система автоматического управления, по принципу отклонения => сигнал ошибки ∆U≈0), поэтому потенциал (.)а равен потенциалу (.)b W(p)=-Z2(p)/Z1(p). Активный фильтр: (УПТ имеет два входа)
знак (-) показывает, что происходит инвентирование. Включая различные Z(p)на входах и в цепь обр св. УПТ можно получить сотни активных типов активных коррект. Устроиств. |
7. Пример составления уравнений для переходного режима В качестве примера - Следящая система множительно -делительного устройства. ЭУ – электр усилитель. D – двигатель пост тока W - угловая скорость двигателя. ОВД – обмотка возбуждающего двигателя Р – понижающий редуктор. α – угол поворота выходного вала редуктора. ПР1 и ПР2 – сдвоенный переменный резистор. UK – напряжение конденсации, т.е. гл отр обратная связь, служащая для формирования сигнала ошибки ∆U. Для облегчения составления уравнения сложной системы ее разделяют на простые элементы и составляют уравнения для каждого из них по отдельности. 1. Уравнение ЭУ: Ug=KY∆U=KY(U1-UK) Ky – коэффициент усиления ЭУ. W(p)=Ky 2. Уравнение двигателя постоянного тока: TЭТМР2W+ TЭРW+W=KgUg W(p)=Kg/(TЭТМР2+ TЭР+1) TЭ – электромагнитная постоянная тока (с),ТМ – электромеханическая пост времени (с), Кg – коэффициент передачи двигателя. 3. Уравнение редуктора: WP=KPW WP – угловая скорость на выходе редуктора. КР – коэффициент передачи редуктора. WP=dα/dt=Pα Pα =KPW W(p)=KP/P 4. Уравнение ПР1: UK=IRX=U2RX/Rn, т.к. резисторы линейные, то для них сравнивается отношение RX/RM=α/αMAX, где αMAX – макс угол поворота двигателя ПР1 UK=αU2/αMAX=Kn α Kn=U2/αMAX Kn- коэффициент передачи. W(P)=Kn По опр передаточной ф-ции имеем UK=KnKP(U1-UK)/(Р(T2P+1)(T1P+1)), приводим это уравнение к стандартной форме: [Р(T2P+1)(T1P+1)+К]UK=KU1 K=KY Kg Kn KP
|
8. Функциональное назначение операционных усилителей. Операционный усилитель осуществляет математическую операцию умножения на постоянный коэффициент. Т.к. в усилителе выполняются некоторые математические операции, то они получили название операционные усилители. Для наглядности и упрощения схем моделирования, принято на схемах не указывать земляной провод, не показывать источники питания, а коэффициент усиления писать внутри резистора. Виды операционных усилителей: 1. Масштабные. 2. Суммирующие 3. Интегрирующие 4. Интегральный суммирующий (подробнее в вопросе №5)
|
|
9.Моделир-еСАУпо диф.ур-ию.Составим схему для реш-я диф.ур-я,описывающего динамику следящей с-мы множительно-делит-ного устр-ва.Было получено ур-е: T1T2(d^3 Uk(t)/dt^3)+(T1+T2)(d^2 Uk (t)/dt^2)+(dUk(t)/dt)+KUk(t)=KU1(t).Алгоритм составления схемы для реш-я этого ур-я:1.Пишем ур-е в операторной форме,т.е.вместо p^n/dt^n пишем p^n.Получим: T1T2p^3 Uk+(T1+T2)p^2 Uk+ pUk+Kuk=KU1.2.Разрешим это ур-е отн-но старшей производной,т.е.найдём p^3 Uk: p^3 Uk=(KU1/T1T2)- ((T1+T2)p^2 Uk/T1T2)-(pUk/T1T2)-(KUk/T1T2)=K1U1- K2p^2 Uk-K3pUk-K4Uk.3.Пусть нам известна правая часть ур-я.Т.к.U1 нужно умножить на К1,то это можно сделать с пом.масштабного операц.усил-ля. –p^2 Uk нужно умножить на К2,что можно сделать с пом.масштабного операц.усил-ля и т.д.. Просуммировав полученные величины с пом. суммирующего операц.усил-ля,на его выходе получим сигнал.Если совместить операцию суммир –я с оперцией интегрир-я,то на выходе получим сигнал –р^2 Uk.Затем продолжаем интегрир-е до тех пор,пока не получим выходной сигнал Uk. Отсюда схема для реш-я ур-я имеет вид:(рис и график).На практике моделир-е САУ по диф.ур-ю почти не использ-ся,т.к.имеет недостатки: теряется наглядность структур.схем; нельзя измерить сигнал на выходе какого-л.из эл-тов САУ; трудно учесть нелин.статические хар-ки,присущие отдельным эл-там САУ. |
10.Модель инерционного звена.W(p)=K/(Tp+1); (X2/X1)=K/(Tp+1); TpX2+X2=KX1; pX2=(KX1/T)-(X2/T )=K1X1-K2X2.Считая известной правую часть, составляем схему для моделир-я: (рис).Эту схему изображаем в виде: (рис).W(p)=(-Z2(p)/Z1(p))=((-R2/ Cp)/(R2/Cp/R1))=-(R2/R1)(1/(R2Cp+1))=-K/(Tp+1); K=(R2/R1); T=R2C. Если известны K,T,то,задавая R2=1мОм,рассчитываем R1,C. |
11. Модель колебательного звена. W(p)=K/(T^2 p^2 +2ξTp+1); (X2/X1)=W(p); T^2 p^2 X2+2ξTpX2+X2=K X1; p^2 X2=(KX1/T^2)-(2ξTpX2/T^2)-(X2/T^2)=K1X1- K2pX2-K3X2.Считая известной правую часть ур-я, строим модель колебат.звена: (рис) |
12.Модель реального диф-щего звена.W(p)=(ĩ p/(Tp +1); (X2/X1)=W(p); TpX2+X2= ĩ pX1; pX1=(dX1/dt). Т.к. идеальных диф-аторов нет,то получить такой сигнал нельзя,=>,нельзя построить модель такого звена.Разделим ур-е на р: TX2+(X2/p)= ĩ X1; X2=( ĩ X1/T)-(X2/Tp)=K1X1-(K2X2/p).(рис). Все модели типовых звеньев можно реализовать при пом. одного операц.усил-ля.но на практике такие схемы не использ-ся,т.к.сущ-ет сложная зависимость м/у коэф-тами модели и коэф-тами передат.ф-ии,что требует больших вычислений.Исключение составляет модель реал.диф.звена: (рис). W(p)=- (Z2(p)/Z1(p))=-(R2/(R1+(1/Cp)))=-(R2Cp/(R1Cp+1))= - ( ĩ p/(Tp+1)). |
|
13. Структурный метод моделирования. (описывается по домашнему заданию) Все модели в тип. схемах можно реализ. при пом. одного операц. усилит., но на практ. такие схемы не исп-ся, т.к. сущ. сложн. зависимость между коэфф-ми модели и коэфф-ми передат. устройств, что требует больших вычисл. искл. – модель реального дифф-его звена. (рис1) Пользуясь структурн. методом моделирования, сост. схему моделирования следящей сист. множит.-делит. Устройства (рис2) Моделирование нелинейных САУ Реальн. элементы САУ имеют нелин. статич. хар-ки, в результате чего сист. Описывается нелин. диф.ур-ем, арифметич. решение кот. возможно лишь в простых случаях (Ур-е 1-ого и 2-ого порядка). Использование моделирования на ЭВМ позв. избеж. этих трудностей. Статич хар-ки реальн. элементов имеют вид: 1) хар-ки типа ограничения (рис3) 2) хар-ки типа нечувств-ти (рис4) 3) хар-ки зоны нечувст-ти с ограничением (рис5) 4) релейная зависимость (рис6) 5) несимметричн. хар-ки (рис7) 6) хар-ка типа люфт (зазор в кинематич. передаче) (рис8) Разработаны электронные модели нелин. статич. хар-к. Для хар-ки типа ограничения эл. модель имеет вид (рис9) Модель типа люфт (рис10) Если в следящ. сист учесть огранич. в электронном усил. и люфт в редукторе, то сх. для моделирования нелин. САУ (рис11) В нелинейных системах возможен новый вид установившегося режима – автоколебания. (рис12) а – амплитуда. Если а мала, то сист. Практически работоспособна, а если велика, то за счёт выбора параметров системы и автокорректирующих устр-в, необходимо учитывать автоколебания. |
14. Преобразование структурных схем. Позволяет существенно упростить нахожд-е передат. ф-ций W(p), Ф(р), Wx(p). Различают: посл-ое соед. звеньев, паралл-е, уст-ва обратной связи. посл соед. зв-ев.: (рис1) Хвых=Wn(p)…W2 (p)W1 (p)Хвых Wпосл(р)=Хвых/Хвх=W1 (p)W2 (p)…Wn(p) (рис2) При паралл. соед. звеньев имеем (рис3) Хвых=Х1+Х2+…+Хn=W1 (p)Хвх+ W2 (p)Хвх+… Wn(p)Хвх Wпар(p)=Хвых/Хвх=W1 (р)+ W2 (р)+… Wn (р) (рис4) Звено, охваченное отриц. связью. (рис5) Передаточн. ф-ция звена обр. связи Хвых=W(p)Х=W(p)(Хвх-Хос)=W(p)Хвх- W(p) Wос(p)Хвых [1+W(p)Wос(р)]Хвых=W(p)Хвх Wохв(p)=Хвых/Хвх=W(p)/ [1±W(p)Wос(р)] Найдём передаточн. ф-цию разомкн. сист. W(p) и замкнутой Ф(р), если структурная система САУ имеет вид (рис6) W(p)=W1 (p) W1 0 (p) W3 (p) W11 (p) W8 (p) Ф(р)=W(p)/(1+W(p) W9 (p)) После приведения к общему заменателю:
Дифференциальное уравнение получится при перемножении числителя первой дроби на знаменатель второй, приравненной к произведению знаменателя первой на числитель второй. Подставляем:
|
15. Связь между различными передаточными функциями. W(Р) – передаточная функция разомкнутой системы. Wp(P) - передаточная функция разомкнутой системы без учета обратной связи. Ф(Р) - передаточная функция замкнутой системы. Wf(P) - передаточная функция по возмещению воздействия. Wx(P) - передаточная функция ошибки. g(t) – входной сигнал, y(t) – выходной, f(t) –сигнал обратной связи. W(P)=Wp(P)Wo(P)
Ошибка системы равна: x(t)=g(t)-y(t)
|
16. Частотные характеристики (общие понятия и определения). Частотные характеристики (ЧХ) определяют динамические свойства звена или системы. Если на вход разомкнутой системы подать гармонический сигнал XBX=XBXSIN(ωt). При прохождении гармонического сигнала ч/з лин сис происходят амплитудные и фазовые искажения, которые можно определить при помощи ЧХ. ХВЫХ=XBЫX SIN(ωt+φ). (рис1) Заменим вх и вых сигналы на их изображение в виде комплексных чисел: XBX=XBXеJ(ωt) ХВЫХ=XBЫX eJ(ωt+φ) W(Jω) – комплексная частотная ф-ция (аналогия передаточной ф-ции), которая получила название амплитудно-фазовой ЧХ (АФК). W(Jω)=A(ω)eJφ(ω) A(ω) – амплитудная ЧХ (АЧХ), φ(ω) – фазовая частотная х-ка (ФЧХ). W(Jω) представляет собой комплексное число, в ней можно выделить вещественную и линейную часть - W(Jω)=U(ω)+JV(ω). U(ω) – вещественная ЧХ (ВЧХ), V(ω) – линейная ЧХ (ЛЧХ). Тогда:
Прологарифмируем W(Jω)=A(ω)eJφ(ω) => lnW(Jω)=lnA(ω)+Jφ(ω) – логарифмическая ЧХ LnA(ω) – логарифм амплитудная х-ка (ЛАХ), φ(ω) – логарифмическая фазовая х-ка. ЧХ позволяют опр источник сигнала, оценивать качество переходного процесса, опр точность САУ, осуществлять синтез корректирующего устройства. |
|
17. Временные характеристики. (общие понятия и определения) Временные характеристики (ВХ) определяют динамические свойства системы. К ВХ относятся – переходная ф-ция h(t) и ф-ция веса W(t). h(t) – это реакция звена или системы на единичный входной ступенчатый сигнал. Такой сигнал явл типовым входным сигналим при исследовании и проектирование САУ. Т.к. характеризует собой наиболее тяжелый режим работы системы. Математически h(t) – это решение дифура звена или системы при единичном ступенчатом сигнале. Если входной сигнал ≠1 и равен XBX=N 1(t), то в линейных системах реакция изменения во столько N раз и будет равна XВЫХ=Nh(t). W(t)
– это реакция звена или системы на δ
– импульс (δ(t)).
δ – импульс – это ∞ тонкий и ∞ высокий
импульс единичной площади. Этот импульс
широко используется при исследовании
и проектировании дискретных систем
управления с ЭВМ в контуре управления.
|
18. Частотные х-ки идеального интегрирующего звена. 1.
Амплит фазовые х-ки: W(P)=K/P
P=Jω
2.
Амплитудные частотные характеристики:
3.
фазовая частотная характеристики:
4.
Логарифм амплит х-ки: (рис)
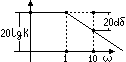
L(ω)=20lgA(ω)=20lg(K/ω)=20lgK-20lgω L(ω=1)=20lgK. Приращение ординаты при изменении частоты на одну декаду: L(10ω)-L(ω)=20lgK-20lg10-20lgω-20lgK+20lgω=20dδ
|
19. Частотные х-ки идеального дифференцирующего звена. 1. Амплит фазовые х-ки: W(P)=KP P=Jω W(Jω)=JKω U(ω)=0 V(ω)=Kω 2. Амплитудные частотные характеристики:
3. фазовая частотная характеристики:
4.
Логарифм амплит х-ки: (рис)
L(ω)=20lgA(ω)=20lgKω=20lgK+20lgω L(ω=1)=20lgK. Приращение ординаты при изменении частоты на одну декаду: L(10ω)-L(ω)=20lgK+20lg10+20lgω-20lgK-20lgω=20dδ
|
20. Частотные х-ки инерционного звена. 1. Амплит фазовые х-ки:
2. Амплитудные частотные хар-ки:
3. фазовая частотная характеристики:
4.Лог ампл х-ки: (рис)
Приращение
ординаты при изменении
частоты на одну декаду (ω=1/Т):
|
|
21. Построение ЛАХ и ЛФК разомкнутой системы (РС). Наиболее простые системы получаются если передаточную функцию РС можно привести к виду (А - кол-во интегрирующих звеньев W(P)=1/P, P=Jω):
Правило построения ЛАХ РС. На низких частотах пренебрегают всеми постоянными времени и рассматривают передаточную функцию W(P)=K/PA. Для построения ЛАХ этого звена из (.), где ω=1, восстанавливаем перпендикуляр = 20 lgK и ч/з получившуюся (.) проводим прямую с наклоном -20Adδ/дек. Эту асимптоту проводим до первой сопрягающей частоты ωi=1/Тi ωJ=1/ТJ , если эта сопрягающая частота соответствует постоянной времени находящийся в знаменателе (что соответствует интегрирующему звену 1/(ТР+1), наклон ЛАХ которого равен -20 dδ/дек). То ЛАХ опускается вниз и проводится до следующей сопрягающей частоты. Если эта сопрягающая частота соотв постоянной времени находящийся в числителе (что соответствует дифференцирующему звену ТР+1, наклон ЛАХ которого равен +20 dδ/дек). То ЛАХ поднимается вверх до следующей сопрягающей частоты и т.д. ЛФК
строится по перемножению, т.к. при
перемножении комплексных чисел
аргументы складываются:
|
22. Необходимое и достаточное условие устойчивости. Устойчивость-устанавливает факт восхожд. или затух. колеб. в сист., при этом не известно о времени перех. процесса, числе колеб. за время перех. процесса… Сист. будет устойчива если при t->∞, xперех.(t)->0, т.е. процесс затухает. Следоват-но устойчивость определяется только общим решением ур-ия (a0dnxвых(t))/dtn+…+anxвых(t)= (b0dnxвх(t))/dtn+…+bnxвх(t), т.е его левой части и не зависит от вх. сигнала. Составл. харак. ур-ие вида: а0рn+a1pn-1+…+an=0; Все корни харак. ур-ия должны нах-ся в левой чпсти комплексной полуплоскости Р, при изменении параметров сист. изменяются значения корней и корни мигрируют на комплексную плоскость. В рез-те чего один или неск-ко корней могут перейти в правую полупоскость и сист. будет неустойчивой.(есть рис.) Для сист. высокого порядка находить корни хар-го ур-ия сложно, поэтому разработаны спец. правила. для систем 1-го и 2-го порядков необх. и достат.чтоб коэф-ты хар-го ур-ия были положительными. для сист. 3-го порядка чтобы произведение средних коэф-ов хар-го ур-ия было больше произведения крайних.(критерий Вышеградского) |
23. Критерий устойчивости Гурвица. Критерий разработан в 1895г. Пусть
определено характеристическое
уравнение замкнутой системы:
Составим главный определитель Гурвица по следующему правилу: по главной диагонали записываются коэффициенты уравнения, начиная со второго по последний, столбцы вверх от диагонали заполняются коэффициентами с возрастающими индексами, а столбцы вниз от диагонали - коэффициентами с убывающими индексами. Остальные места заполняются нулями. В случае отсутствия в уравнении какого-либо коэффициента и вместо коэффициентов с индексами меньше 0 и больше n пишут нуль. Системы первого и второго порядка устойчивы, если все коэффициенты характеристического уравнения больше нуля. Система находится на грани устойчивости, если ∆n=0 и все диагональные миноры положительны: в этом случае an=0 (апериодическая граница устойчивости). Если ∆n-1=0, а an≠0 и все остальные диагональные миноры положительны, то система на границе устойчивости (колебательная граница устойчивости). Для устойчивости системы необходимо и достаточно, чтобы при положительном коэффициенте характеристического уравнения a0 главный определитель Гурвица и все его диагонали миноры были положительны. Если хотя бы один из коэффициентов или один из определителей отрицательны, то система устойчива. Если один из коэффициентов либо один из определителей равны нулю, то система на грани устойчивости. Критерий Гурвица удобен для исследования устойчивости систем третьего и четвертого порядков, когда известны параметры системы. |
24. Пример исследования устойчивости по критерию Гурвица. (рис1) Структурная схема множительно-делительного устройства Передат. ф-я разомк. сист.равна:W(p)=(kykgkpkn)/((T1p+1) (T2p+1)p)=k/((T1p+1) (T2p+1)p) Передат. ф-я замкн. сист. Ф(р)=W(p)/(W(p)+1)=k/((T1p+1) (T2p+1)p+k) Тогда харак. ур-ие: Т1Т2р3+( Т1 +Т2)р2+р+к=0 Или для получения харак. ур-я достаточно сложить числитель и знаменатель передат. ф-ции разомкн. сист. и приравнять к нулю. Так как сист. имеет характ. ур-е 3 порядка, то для исследования устойчивости воспольз. Критерием вышнеградского Т1+Т2Т1Т2К 1/Т1+1/Т2К Если Ккр=1/Т1+1/Т2, то сист. будет находиться на границе устойчивости и в ней возникают незатухающие гармонические колебания. Коэффициенты, при кот. Сист. находится на гр. устойчивости – критические. Практич. Использование критерия Гурвица ограничивается уравнениями 4 порядка, т.к. при дальнейшем повышении порядка условия устойчивости по Гурвицу настолько сложны, что трудно определить, какой коэффициент и насколько надо изменить, чтобы система стала устойчивой. В этих случаях используются др. критерии устойчивости. |
|
25. Критерий устойчивости Михайлова. Устойчивость
замкнутой САУ определяется
характеристическим полиномом:
Согласно
принципу аргумента для устойчивой
системы
При
изменении
от
Можно
показать, что функция u()
четная, а ()
нечетная. Поэтому
Формулировка
критерия Михайлова.
Система устойчива, если при изменении
от 0 до
|
26. Пример исследования устойчивости по критерию Михайлова. (рис) Примером служат картинки, где кривая проходит \ не проходит через все квадраты по порядку. |
27. Критерий устойчивости Найквиста. Критерий базируется на частотных характеристиках разомкнутой цепи САУ, так как по виду частотных характеристик разомкнутой цепи можно судить об устойчивости замкнутой системы. Система, устойчивая в разомкнутом состоянии. Если разомкнутая цепь системы устойчива, то для устойчивости замкнутой системы необходимо и достаточно, чтобы амплитудно-фазовая частотная характеристика разомкнутой цепи не охватывала точку (-1, j0). Система, имеющая полюсы на мнимой оси в разомкнутом состоянии. Если разомкнутая цепь системы имеет нулевые и чисто мнимые полюсы, то для устойчивости замкнутой системы необходимо и достаточно, чтобы амплитудно-фазовая частотная характеристика разомкнутой системы с ее дополнением в бесконечности не охватывала точку (-1, j0). Система с неустойчивой разомкнутой цепью. Для устойчивости замкнутой системы требуется, чтобы амплитудно-фазовая характеристика разомкнутой цепи (с дополнением в бесконечности для нейтральных систем) охватывала точку (-1, j0) против часовой стрелки на угол m, где m - число полюсов с положительной вещественной частью в передаточной функции неустойчивой разомкнутой цепи системы. |
28.Исследование устойчивости при помощи ЛЧХ.Исследования критерия Найквеста осуществляются при помощи АЧХ\ФЧХ. (рис) Для
устойчивости системы n-ного
порядка необход и достат., чтобы для
всех частот, при которых ординаты
ЛАХ>0 , ЛФХ не пересекала линию - |
|
29. Понятие о качестве системы.Основным показателем, определяющем пригодность системы к эксплуатации является устойчивость. Но устойчивая система может иметь не достаточное быстродействие, большое число колебаний, недостаточную точность. Для каждого случая пригодность системы определяется точностью и характером переходного процесса. Точность САУ хар-ся величинами ошибок, в установившихся и вынужденных режимах, которые имеют место после окончания переходного процесса. Переходный процесс принято рассматривать как реакцию системы на единичный ступенчатый сигнал, характеризующий наиболее тяжелый режим работы системы. Основными качественными показателями переходного процесса явл время переходного процесса tn , перерегулирование δ(%), число колебаний за время переходного процесса m. Эти показатель легко определить по кривой переходного процесса(рис). tn - это время, по истечению которого выходная величина становится меньше заданной величины ∆ (обычно ∆=(5-10)% от входного сигнала). Для определение качественных показателей по кривой переходного процесса требует решения дифуров, а при выборе параметра требует решения нескольких дифуров, поэтому разработаны приближенные оценки кач-ва переходного пр, которые не требуют решения дифуров. |
30. Частотные оценки качества переходного процесса.Оценка качества по частотным хар-кам не рассматривает конкретного вида перех. процесса, а базируется на некоторых частотных св-вах сис-мы. Наиболее хорошо они разработаны в отношении оценки запасоустойчивости. Запас устойчивости предусматривает такое удаление расчётных параметров с-мы, от значений соотв. границы устойчивости, чтобы была обеспечена работоспособность реального образца, наиболее просто запас устойчивости определяется по АФХ разомкн. с-мы, при этом вводятся понятия: запас устойчивости по модулю (β) и по фазе (μ). Пусть АФХ разомкн. с-мы имеет вид (рис.). Аналитической связи между β,μ,δx,tn установить не удалось, но практикой эксплуат. реальных систем β=2÷10; μ=(30÷60)0, то в с-ме будут наблюдаться 1-1,5 колеб. То переходный процесс будет иметь вид (рис.) tn≈(1÷2)*2π/ωср.. Запасы устойчивости по модулю так же можно легко определить по ЛАХ и ЛФХ разомкнутой системы. (рис.) Существуют и др. оценки качества по частотным хар-кам. |
31. Интегральная оценка качества переходного процесса.Интегральн. оценки качества так же не рассматривают конкретного видопереходного процесса, а базируются на некоторых интегральных св-вах с-мы, т.е. они учитывают быстродействие и перерегулирование совместно без определения того или иного в отдельности. Простейшей интегр. оценкой явл. оценка вида: I1=∫∞0 x(t)dt, где x(t)- ошибка с-мы. x(t)=g(t)-y(t); (рис.) геометрически этот интеграл равен площади от кривой переходного процесса, построенного для ошибки. Поэтому параметры с-мы следует выбрать так, чтобы обеспечить минимум этой интегральной оценки, однако эта оценка даёт удовл. результаты только для не колебательных процессов, т.к. в колеб. процессах площади алгебраически складываются и минимум этой интегр. оценки будет соответствовать с-ме с большой колебательностью. (рис.)Поэтому разработаны др. интегральные оценки: I2=∫∞0 |x(t)|dt; (рис.) Параметры с-мы вибираются так, чтобы обеспечить минимум этой интегральной оценки. Но вычислить этот интеграл аналитически невозможно, но использование ЭВМ позволяет избежать этих трудностей. С-ма для нахожд интегр оценки имеет вид: (рис) 1 из возможных схем БМ имеет вид: (рис) С помощью этой сх необх построить зависимость I2=I2(A), где А-параметр, подлежащий выбору. Пусть А=К(коэф усиления разомкн с-мы). Предавая параметру А различные фиксированные значения, для каждого из них определяем величину интегральной оценки и по получ данным строим зависимость I2=I2(К), например вида: (рис). Чем больше К, тем больше колебательность, при малых К колебательность затянута. (рис) Если переходный процесс построенный при К близком к оптим, не будет соотв техн заданию, то в с-му необх ввести коректир устройства и выбрать параметры коректир устройства чтобы удовл коректир параметры техн заданию. Пусть Wку(p)=K(T1P+1)/P(T2P+1)2; Одной из интегр оценок явл квадратичная интегр оценка вида I1=∫∞0 [x(t)2]dt (рис)Параметры с-мы следует выбирать так, чтобы получить минимум этой инт оценки. Этот инт определяется теоретич по коэфиц передат ф-ции замкн с-мы. В ряде случаев с-мы параметры в которых выбраны с помощью этих интегр оценок, являются всё же слишком колебательными, поэтому разработаны улучш интегр оценки, которые учитывают даже скорость изменения ошибки. |
32. Точность САУ в типовых режимах (неподвижное состояние).Этот режим может сущ при постоянных управляющих и возмещающих воздействиях g(t)=g0=const; f(t)=f0=const; При отраб этих сигналов, появляется ошибка x(t), которая получила название статической, а так же все производные от постоянной величины=0, то P=d/dt=0; Системы, которые имеют остаточную ошибку получили название статических с-м. Найдём выражение для ошибки из обобщенной структурн схемы САУ, которая имеет вид (рис) WR-перд ф-я регулятора; WO-перд ф-я обьекта регулирования. Ошибка равна: x(t)=g(t)-y(t)=g(t)-W0(p)[f(t)+z(t)]=g(t)-W0(p)f(t)-W0(p)WR(p)x(t); x(t)=g(t)/(1+W(p))+W0(p)/(1+W(p))-f(t); Тогда статическая ошибка будет равна: xст=|1/(1+W(p))|g0+| W(p)/(1+W(p))|f0=xст1+xст2. При постоянных управл и возмущ воздействий возникают 2 сост статич ошибки. Рассмотрим первую составляющую стат ошибки. Первая ф-я разомкн с-мы имеет вид: W(p)=(b0pm+b1pm-1+…+bm-1p+bm)/(a0pn+a1pn-1+…+an-1p+an); Если m>n, то это говорит о физической нереализуемости системы, т.к в этом случае должны присутствовать идеальн конденсаторы с перед ф-ей W(p)=τp; W(p)=K*R(p)/Q(p). Если К впереди, то R(p) и Q(p)=1; Тогда W0=K; xст1=(1/(1+W0))g0=g0/(1+K); Для уменьш статич ошибки необх увелич коэф усиления разомкн с-мы. Но при этом мы приближаемся к Ккритич и с-ма может стать неустойчивой; (рис). Введём преждевременно в с-му интегр звено. (рис). Тогда статич ошибка1=0, но интегрир звено вносит дополнительный фазовый сдвиг -π/2, что приводит к уменьшению запаса устойчивости и с-ма может быть неустойчивой. С-мы, которые не имеют статич ошибки получили название статические, при наличае в с-ме n интегр звеньев, с-ма назыв астатической n-ого порядка. (рис). Рассмотрим 2-ю составл статич ошибки, при этом возможны следующие случаи: объект и регулятор – статические. Wp(p)=Kp*Rp(p)/Qp(p); W0(p)=K0*R0(p)/Q0(p); Тогда xст2=(K0/(1+KpR0))*f0=K0/(1+R)*f0; (рис). Введём преднамеренно в регулятор интегрирующие звено, тогда: Wp(p)=K*Rp(p)/p*Qp(p); xст2=0; (рис). |
|
33. Точность САУ в типовых режимах (движение с постоянной скоростью).Этот режим может существовать при изменении управляющего воздействия с постоянной скоростью.g(t)=vt, v=const. (рис1)Такой сигнал является типовым при исследовании и проектировании следящих систем. Ошибка системы в этом режиме называется скоростной x(t)=xск. V и xск задаются в ТехЗад на проектировании исходя из конкретного технологического процесса. Найдем диф.ур. для ошибки, используя передаточную ф-ию ошибки. Wx(p)=x(t)/g(t)=1/(1+W(p)). В общем случае: W(p)=kR(p)/[pQ(p)], где - кло-во интегрирующих звеньев или порядок астатизма. =0 – статич.с-ма, =1 – астатизм 1-го порядка. X(t)/g(t)=1/[1+kR(p)/(pQ(p))=Q(p)*p/(pQ(p)+kR(p)); [pQ(p)+kR(p)]x(t)=Q(p)*pg(t) (1); ДУ для ошибки:1) =1 тогда [pQ(p)+kR(p)]x(t)=Q(p)pg(t)= Q(p)*dg(t)/dt=Q(p)dvt/dt=Q(p)v=v (2) пусть x(t)=xск=v/k подставляем в (2): k*v/k=v, т.е. подобранное значение является частным решением ДУ. (рис2) 2. [p2Q(p)+k*R(p)]x(t)= Q(p)p2g(t)=Q(p)d2g(t)/dt=Q(p)d2vt/dt2=0 (3) т.к. у-е (3) является однородным, то отсутствует частное решение, а следовательно будет=0 скоростная ошибка, но второе интегрирующее звено вносит доп. фазовый сдвиг -/2, что приводит к уменьшению запаса устойчивости и с-ма может стать неустойчивой, т.е. существует противоречие между устойчивостью и точностью. (рис3) |
34. Коэффициенты ошибки Wx(p)=x(p)/C(p)=1/(1+W(p)), x(p)-изображение ошибки, C(p)-изображение управляющего воздействия. X(p)=[1/(1+W(p))]C(p); x(p)=(C0+C1p+C2p2/2!+…)C(p) (1)Переходя от изображений к оригиналам, получим выражение для установившейся ошибки xуст= C0g(t)+C1dg(t)/dt+C2d2g(t)/(2!dt2)+…; C0-статич.ошибка(для аститич.с-мы C0=0); C1-скорост.ошибка;C2-ошибка от ускорения и т.д. Коэффициенты ошибок легко получить путем деления перед. ф-ии на знаменатель и сравнении получ.ряда с рядом (1).Пример: W(p)=k/[(T1p+1)(T2p+1)p], тогда Wx(p)=1/[1+W(p)]+1/[1+k/((T1p+1)(T2p+1)p)]= [T2T1p3+(T2+T1)p2+p]/[ T2T1p3+(T2+T1)p2+p+k]; C0=0; C1=1/k; C2/2!=( T2+T1-1/k)1/k |
35. Повышение порядка астатизма.физически повышение порядка астатизма осуществляется за счет введения в с-му интегрирующих звеньев. При этом можно регулировать как статическую, так и скоростную ошибки. Введем преднамеренно в следящую с-му мду интегр. звено с перед. ф-ей Wи=kи/p=1/(Tиp), где Tи-постоянн. интегрирован. Тогда структурн.схема следящ.с-мы имеет вид (рис1) W(p)=(kуkрkиkдkп)/[(T1p+1)(T2p+1)p2] =z; при =2 и 2-м порядке астатизма будет ликвидироваться скоростн.ошибка. Характерист.уравн: T1T2p4+(T1+T2)p3+p2+k=0. С-ма неустойчива, т.к. не вып-ся необходимое, но не достаточное условие устойчивости (все коэф-ты характ-кого у-я замкн. с-мы должны быть >0). С-мы, в к-рых нельзя обеспечить устойчивость за счет изменения пар-ров с-мы наз-ся структурно неустойчивыми и для обеспечения их устойчивости необходимо изменить структуру САУ. В данном примере неустойчивость физически объясняется тем, что каждое интегрирующее звено вносит фазовый сдвиг -/2 или 2 звена вносят сдвиг -, в результате чего обратная связь из отрицательной превращается в положительную. Существует др.путь повышения порядка астатизма без заметного уменьшения запаса устойчивости. Этот путь состоит в применении изодромных устройств. При таком способе дополн.интегр.звено вкл.е последов,в параллельно. Структ.схема САУ в этом сл.будет иметь вид: (рис2) Wи(p)=1+kи/p=(p+kи)/p=k*(p/kи+1)/p= Tиp+1/Tиp; перед.ф-ия разомкн.с-мы будет равна: W(p)=[kуkиkрkпkд(Tиp+1)]/[(T1p+1)(T2p+1)p2]. Характ.у-е: (T1p+1)(T2p+1)p2+kTиp+k=0. Появился коэф-т при р. Можно обеспечить устойчивость за счет выбора параметров с-мы. Физически это объясняется тем, что изодромное устройство всегда имеет фазовый сдвиг, отличный от -/2 и обратная связь остается отрицательной. из=-/2-arctgTи. порядок астатизма остался=0. Для дальнейшего повышения порядка астатизма можно использовать несколько изодромных устройств. |
36. Регулирование по производным от ошибок.Структурн.схема САУ с введением производной: (рис1)ДУ- дифференцирующее устройство, например (рис2) (рис3)W(p)=p/Tp+1; T0;Сигнал ошибки будет=0 в точке А, но вследствие инерционности с-мы продолжается движение в прежнем напр-ии. Возникает ошибка другого знака и возн.колебания.Для сглаживания колебаний и повышения быстродействия САУ введем в с-му диф-ее звено, сигнал к-рого будет изменяться по закону (кривая.2). на участке возрастания ошибки x(t) сигналы x(t) и dx(t)/dt складываются, что увеличивает порцию сигнала от регулятора и с-ма начинает эффективнее отрабатывать ошибку. На участке уменьш.ошибки x(t) произв. изм. свой знак и вычитается из сигн.ошибки. в определенный момент x(t) будет=dx(t)/dt, а дальше движение идет по инерции (кривая 3, условно). Т.к. производная повышает запас устойчивости, то это позволяет увеличить коэфф-т усиления с-мы и тем самым повысить точность. Введение производных законов упр-я также позволяет из неустойчивой с-мы получить устойчивую. |
|
37.ПИД-закон регулир-ия. инт-ал повыш. точность сис-мы, но уменьш. запас уст. и сис-мя стан-ся колеб-ой. чтобы увел. запас уст-ти в з-н регул. вв. произв. от ош-ки, тогда САУ имеет вид:(рис.) зак-н рег-ия: z(t)=kpx(t)+gdx(t)/dt+1/Tux(t)dt. Регул. возд. пропорц. сигн. ош-ки, произв. от ош. и интегр. от ош., поэтому такой з-н рег-ия наз. пропорционално-интегрально-диф.(ПИД) Настройки рег-ра kp, g, Tu выбир-ся в зав-ти от придат. ф-ии объекта регул-ия.При этом если трудно сост-ть мат. модель, разработаны методы эксперим-ого опред-ия передат. ф-ии. Если отсутствуетдеференциатор имеем ПИ(пропорционально-интеграторный)-регулятор;ПД- и П-регуляторы. |
38.Коррекция сис-м упр-ия. (общие понятия и определения) Исп-ся не только для обеспечения заданной точн-ти, но и для обеспечения желаемого кач-ва перех. процесса. Различают: посл. коррект. устр-во; паралл. коррект. устр-во; устр-ва обратной связи. Послед. коррект. устр-во. Прим-ся в тех случаях,когда в сис-ме исп-ся сигнал в виде напр-ия пост. тока.Корректир.устройства реализуются с пом-ю простых RC-фильтров Жёсткие обратные связи.Обратная связь – устройство, передающ. возд. от какого-либо последующ. элемента на вход одного из предыдущ. звеньев и по методу присоединения делятся на положит. и отрицат. |
39.Послед. коррект. устр-во. Прим-ся в тех случаях,когда в сис-ме исп-ся сигнал в виде напр-ия пост. тока.Корректир.устройства реализуются с пом-ю простых RC-фильтров Сущ. сотни разл. типов коррект. уст-в, кот. с физ. точки зрения либо усил. вх. сигнал в опред. полосе частот, либо ослабл., внос. + или – фазов. сдвиг, что привод. к деформир. АФХ исх. сис-мы, и за счет выбора парам. коррект. устр-в добив-ся необх запаса уст-ти. Посл. дифференц. звено. (рис1) W(p)=z2(p)/(z1(p)+z2(p))=k0(T1p+1)/(T2p+1) Схема имеет вид (рис2) w(p)=k0k(T1p+1)/(T2p+1)(Tp+1) Пусть T1=T W(p)=k0k/(T2p+1) Можно умен. инерц. звена, что повыш. запас уст. и быстрод. сис-мы. Посл. интегро-дифф. звено. (рис3) W(p)=(T1p+1)(T3p+1)/(T2p+1)(T4p+1) На низк. и выс. част-ах звено не искаж. вх. сигнал, а на средн. част-ах происх. значит. ослабл. вх. сигнала.(рис4) |
40. Жёсткие обратные связи.Обратная связь – устройство, передающ. возд. от какого-либо последующ. элемента на вход одного из предыдущ. звеньев и по методу присоединения делятся на положит. и отрицат.Простая жёсткая обр. связь описывается уравн. Yoc=Koc+Xoc WKoc(p)=Koc Простая жесткая обратная связь: Пусть имеется усил-ль мощности с коэфф. усил-я 10 (рис1). Усил-ль с таким коэфф. усил-я можно получить, если ввести предварит. Усил-ль и охватить их жёстк. Обр. cв-ю. (рис2) В следствие старения элементов нестабильности источника питания и т.д. коэфф. усил-я мощности изм. В 2 раза и стал равен 5. А в усил-ле, охв. Обр. св., коэфф усил-я будет равн 9,9. За счёт обр. связи можно значит. снизить влияние нестабильности параметров охватываемого звена. Охватим инерц. Звено простой ЖОС (рис3)
За счёт выбора Кос можно существенно уменьш. инерц-ть охватываемого звена, что повышает запас устойчивости и быстродействия системы, но во столько же раз уменьшается коэфф. усил-я, что приведёт к понижению точности системы, а это недопустимо, потребуются дополнительные каскады усиления, это приведёт к повышению стоимости, габаритов, к уменьшению надёжности. |
|
41. Инерционные жёсткие обратные связи. Инерционная ЖОС описывается уравнением
|
42. Гибкие обратные связи. Гибкие
обратные связи – исчезающие, т.к. они
действуют только во время переходного
процесса.Охватим простое инерционное
интегрир звено простой гибкой обратной
связью (рис1)
При таком охвате тип звена не изменился, что очень важно, так как сохранился порядок астатизма, а за счёт выбора Кос можно существенно уменьшить инерционность звена, что позволяет повысить запас устойчивости и быстродействие системы, но при этом уменьшается коэффициент усиления системы, что недопустимо, поэтому потребуются дополнительные каскады усиления. Охватим
инерционное звено простой гибкой ОС
(рис2)
Увеличивается постоянная времени охватываемого звена, уменьшается запас устойчивости и быстродействия, поэтому не всякая ОС может дать положительный эффект. |
|
|



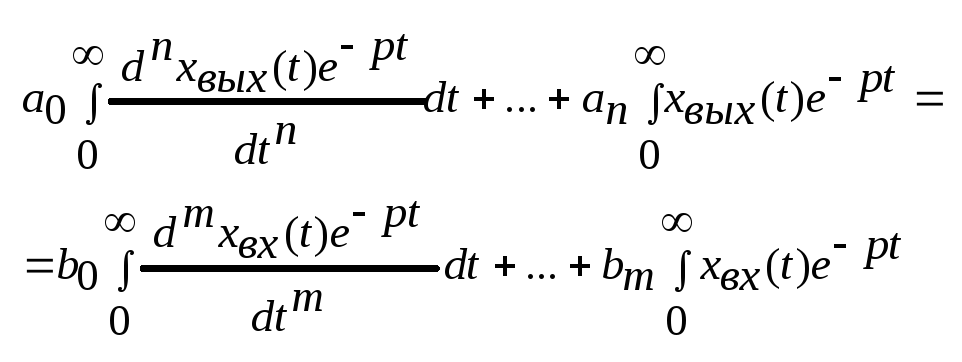



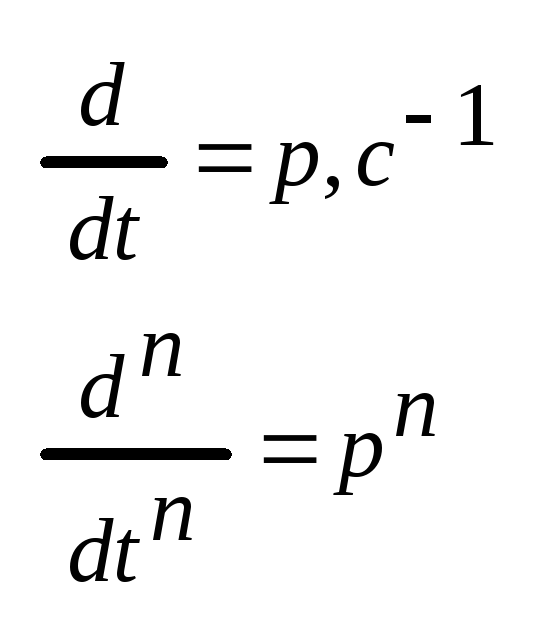 где
P
– символ или оператор дифференцирования.
где
P
– символ или оператор дифференцирования.





 U2=-U1/TP
Если задан коэфф. Усиления K,
то К=1/T=1/RC,
задаваясь R=1мОМ,находим
с,мкФ
U2=-U1/TP
Если задан коэфф. Усиления K,
то К=1/T=1/RC,
задаваясь R=1мОМ,находим
с,мкФ k=R2/R1
T=R2C
k=R2/R1
T=R2C

 20dδ/дек
20dδ/дек

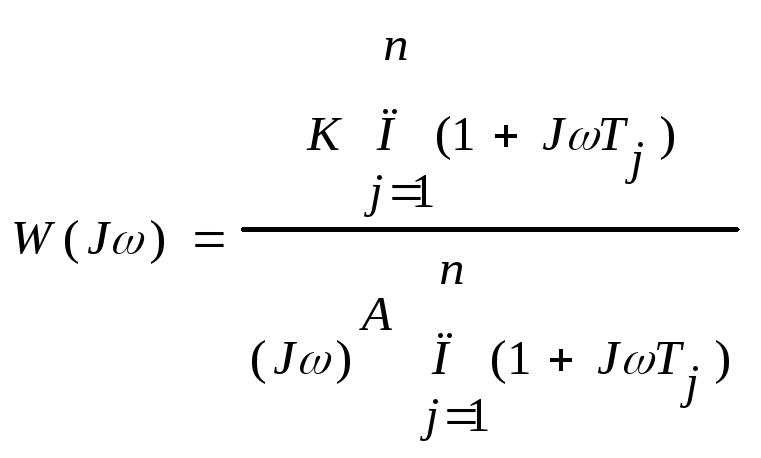 L(ω)дб=20lg|W(Jω)|
L(ω)дб=20lg|W(Jω)|

