2. Нагревательный элемент е104

Процессы, происходящие в резервуаре, описываются уравнением теплового баланса [1]:

(2.1)

С – теплоёмкость объекта,

А – теплоотдача объекта,

 – температура,

Q – подводимая к объекту тепловая энергия.

Процесс нагревания элемента описывается уравнением:

- Закон Джоуля-Ленца (2.2)

Преобразовав уравнение, запишем:

(2.3)

Подставим получившееся выражение в уравнение (2.1)

Cd + Adt=dt

Преобразуем в операторную форму (p=)

(Tp+1) (t) = kd

Получаем передаточную функцию нагревательного элемента

W_им(p)=k/ (Tp+1) (2.4)

Вычислим коэффициент усиления и постоянную времени

По справочным данным [3]:

C=307 ДЖ /(кг·К)

А=2950 ДЖ/( кг·К) ·с

По формуле (1.3) получаем : Т_им=0,1

По формуле (1.4) получаем: k_им=0,3

В итоге передаточная функция данного элемента будет иметь вид:

W_им(p)=0,3/ (0,1p+1) (2.5)

3. Датчик температуры на базе термопары дТпl 015

Для описания нагрева тела термопары используем уравнение теплового баланса[1]:

(3.1)

С - удельная теплоемкость термопары,

А - коэффициент теплоотдачи термопары,

- измеряемая температура,

–измеряемая температура.

Преобразование температуры в термоЭДС опишем приближенной зависимостью[1]:

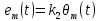(3.2)

На основе (3.1) и (3.2) запишем дифференциальное уравнение для термопары. Для этого из (3.2) выразим температуру тела термопары через э.д.с.:

И подставим в уравнение (3.1):

Преобразуем последнее уравнение, использую операторную форму записи:

(T_тp+1)e_т(t)=k_тθ(t) (3.3)

где - постоянная времени термопары;

–коэффициент преобразования термопары.

На основании (3.2) запишем передаточную функцию для термопары:

(3.4)

Термопара представлена типовым инерционным звеном.

Входным сигналом является температура в резервуаре, выходным - напряжение. Максимально допустимая температура по технической характеристике резервуара равна 90ºС, минимальная 12°С. Напряжение на выходе равно 24В. Коэффициент преобразования термопары:

По техническим характеристикам [3] определяем постоянную времени: T_т=10с.

Передаточная функция для термопары:

(3.5)

1.3.4 Описание регулятора

Передаточную функцию регулятора W_р(p) принимаем равное 1, так как регулятор в системе пока отсутствует, но будет добавлен при дальнейшем исследовании [1].

3. Структурная схема и передаточная функция системы

На основе функциональной блок-схемы (рис.5) и описание элементов передаточными функциями, составляем структурную схему исследуемой системы, изменив условные обозначения звеньев на конкретные выражения их передаточных функций. По структурной схеме (рис.6) определяем передаточную функцию разомкнутой системы и передаточную функцию замкнутой системы.

_{Рис. 6 – Структурная схема системы.}

Преобразуем полученную структурную схему к замкнутой системе с единичной обратной связью с целью получения передаточной функции замкнутой системы. Для этого перенесем сравнивающий элемент с выхода датчика на вход, при этом необходимо между переносимым задающим воздействием и сравнивающим элементом добавить фиктивное звено с передаточной функцией, обратной передаточной функции исходного звена, находившегося в обратной связи (рис.6). Из рисунка видно, что выходной сигнал фиктивного звена не оказывает на динамические свойства системы никакого влияния, так фиктивное звено расположено до сравнивающего элемента. Поэтому в дальнейшем можно не учитывать фиктивное звено при описании передаточной функции системы (рис. 8).

Рис. 7. Преобразованная структурная схема системы.

Рис. 8. Преобразованная структурная схема системы без фиктивного звена.

В соответствии с полученной структурной схемой, а так же правилами нахождения передаточной функции соединения звеньев[2], передаточная функция разомкнутой системы будет иметь вид:

W(p) = ∏Wi(p) (4.1)

или:

W(p) = W_д(p)·W_р(p)·W_им(p)·W_Об(p) (4.2)

Подставив значения передаточных функций звеньев, получим передаточную функцию разомкнутой системы:

W(p)=W_р·W_им·W_об·W_д (4.3)

где: k= 0.018-общий коэффициент передачи системы.

T_д= 10 ; T_им=0,1 ; T_об=0,54 – постоянные времени датчика, исполнительного механизма и объекта управления соответственно.

Значение W_р(p) примем равное 1, так как в системе регулятор пока отсутствует, но будет добавлен в дальнейшем.

Передаточная функция замкнутой системы определится по формуле [2]:

Ф(р)=W(p)/(W(p)+1) (4.5)

G(p) – характеристический полином системы