4.2. Построение модели дп

Общими рекомендациями при построении модели ДП являются следующие.

1. Выбираем способ деления процесса на шаги.

2. Вводим параметры состояния и переменные управления на каждом шаге .

3. Записываем уравнения состояний (зависимость конечного состояния -го шага от начального состояния -го шага и от управления на -м шаге )

.

4. Из ограничений задачи определяем для каждого -го шага множества допустимых управлений .

5. Вводим показатели эффективности каждого шага и суммарный показатель .

6. Вводим условные максимумы (минимумы) показателя эффективности на шагах от -го шага до конца процесса и условные оптимальные управления на -м шаге .

7. Записываем уравнения Беллмана:

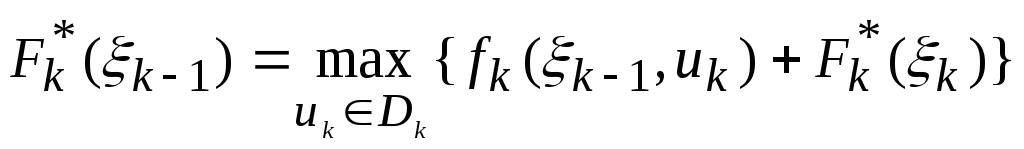, , (23)

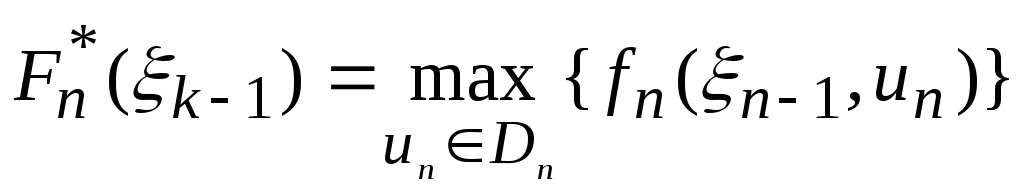, (24)

где - максимум показателя эффективности на шагах от -го шага до конца процесса при условии, что начальное состояние -го шага . Управления, на которых реализуются максимумы в (23), (24), обозначаем и называемусловными оптимальными управлениями на шагах .

4.3. Построение вычислительной схемы дп

Уравнения Беллмана (23),(24) лежат в основе алгоритма решения задачи ДП, который состоит из двух этапов [4,6].

Этап . Условная оптимизация (движение от конца к началу).

Последовательно вычисляем по уравнениям (22),(23) ; ;…; для всех допустимых на соответствующих шагах состояний . Причем

при определении значений учитывается найденная из предыдущей задачи (22), (23) функция

Этап . Безусловная оптимизация (движение от начала к концу).

Используя уравнения состояний и то, что начальное состояние фиксировано, находим последовательно безусловные оптимальные управления на каждом шаге :

4.4. Несколько замечаний к методу дп

Большим достоинством метода ДП является возможность анализа чувствительности к изменению исходных данных и . При изменении этих данных задача не решается заново, а делаются лишь некоторые добавления.

Так, если число шагов увеличивается на единицу, то достраиваем схему, снабдив новый шаг индексом 0, а начальное состояние этого шага будет . Суммарный максимум шагов равен.

Иногда вычислительный процесс условной оптимизации удобно строить от 1-го шага к -му. Это прямой ход вычислений, в отличие от рассмотренного выше - обратного хода. Уравнения состояний и уравнения Беллмана для прямого хода имеют вид:

,

, , .

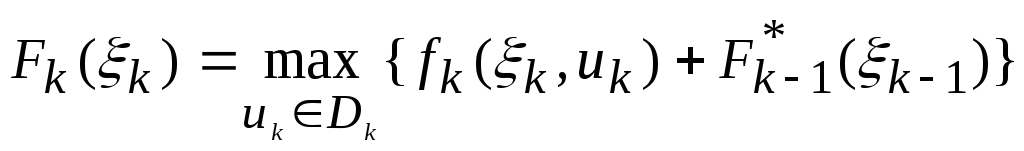Безусловное оптимальное управление определяется, начиная с .

С точки зрения объема вычислений обе схемы равноправны, но при некоторых дополнительных исследованиях предпочтительнее становится та или другая. Так, добавление новых шагов удобнее проводить при прямом ходе. Для исследования чувствительности задачи к начальному состоянию удобнее обратный ход, а для исследования чувствительности к конечному состоянию удобнее прямой ход.

4.5. Задачи распределения ресурсов

В общем виде эти задачи имеют следующую содержательную формулировку.

Имеется некоторое количество ресурсов (денежные средства, сырье, трудовые ресурсы, различные виды оборудования и т.п.). Эти ресурсы необходимо распределить между различными объектами их использования по отдельным промежуткам планового периода так, чтобы получить максимальную суммарную эффективность от выбранного способа распределения. Показателем эффективности может служить прибыль, товарная продукция, фондоотдача для задач максимизации или суммарные затраты, себестоимость, время выполнения для задач минимизации.

Рассмотрим одну конкретную задачу распределения ресурсов.

Планируется распределение начальной суммы средств между предприятиями . Выделение -му предприятию средствприносит доход,. Определить какое количество средств нужно выделить каждому предприятию, чтобы обеспечить максимальный суммарный доход.

Математическая модель задачи имеет вид:

,

, .

,

Построим модель ДП.

Распределение средств между предприятиями можно рассматривать как -шаговый процесс. Поэтому за номер -го шага процесса примем номер предприятия, которому выделяются средства . Очевидно, что переменные ,, можно рассматривать как управляющие переменные.Начальное состояние системы характеризуется начальной величиной средств . В конце первого шага состояние системы характеризуется остатком средств после выделения 1-му предприятию средств . Величины , характеризующие остаток средств после распределения на соответствующих шагах, рассматриваем как состояния системы.Уравнения состояний в данном случае имеют вид:

, .

Конечное состояние , т.е. все средства , оставшиеся к -му шаг, выделяются -му предприятию: .

Найдем допустимые управления на -м шаге. Предприятию можно выделить любое количество из имеющихся к началу шага средств.Поэтому допустимое управление удовлетворяет неравенствам .

Показателем эффективности каждого шага является доход , суммарным показателем - суммарный доход . Тогда условным максимумом будет максимальный суммарный доход на шагахпри начальном состоянии-го шага. Условное оптимальное управлениебудет определять оптимальное количество средств, выделяемых-му предприятию, если остаток средств для распределения предприятиямравен.

Запишем теперь уравнения Беллмана

, , (25)

, (так как ). (26)