Лабораторная работа № 6.21к

Изучение явления резонанса в последовательном колебательном контуре.

Цель работы: изучить зависимость напряжения на конденсаторе последовательного колебательного контура от частоты вынуждающей ЭДС; определить по результатам измерений параметры колебательного контура.

Работа выполняется на ЭВМ

Краткие теоретические сведения

Последовательный колебательный контур состоит из конденсатора емкостью С, катушки индуктивностью L, омического сопротивления R и источника переменной ЭДС , включенных между собой последовательно (рис.1).

Вынуждающая гармоническая ЭДС изменяется по закону  = _оSint, где  - частота переменной ЭДС. Составим дифференциальное уравнение, описывающее колебательный процесс в рассматриваемом контуре, использя второе правило Кирхгофа.

IR + U_c =  +_s , (1)

где U_c- напряжение на емкости, _s- ЭДС самоиндукции, возникающая в катушке индуктивности. Силу тока в цепи и напряжение на конденсаторе можно связать, рассматривая процесс изменения заряда конденсатора.

. (2)

Подставляя (2) в (1), получим

. (3)

Введем обозначения: R/2L=, 1/LC=_o² и _o/LC=E_o (_о- частота собственных колебаний контура, - коэффициент затухания). После подстановки в (3) получим неоднородное дифференциальное уравнение вынужденных колебаний

, (4)

решением которого является сумма частного решения неоднородного уравнения и общего решения соответствующего однородного уравнения, которым в установившемся режиме можно пренебречь. Частное решение уравнения (4) имеет вид:

U_c = U_c()sin(t +), (5)

где:

, (6)

. (7)

Uc()-амплитуда вынужденных колебаний напряжения на емкости,

- сдвиг фаз колебаний напряжения на емкости по отношению к колебаниям вынуждающей ЭДС. Вынужденные колебания происходят с частотой вынуждающей ЭДС. Исследование зависимости Uc от  показывает:

1. при   0 напряжение на емкости U_c _о;

2. функция U_c=U_c() обладает максимумом U_c^max при частоте генератора _р =(доказать самостоятельно);

3. при    напряжение на емкости U_c 0.

Зависимость напряжения на емкости от частоты вынуждающей ЭДС носит название резонансной кривой. Положение максимума резонансной кривой зависит от коэффициента затухания (рис.2).

Д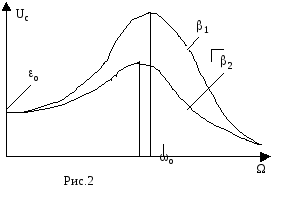ля колебательного контура вводится понятие добротности, которая определяется как

Q = U_o^max/_o. (8)

Или

Q = , (9)

где R_к – сопротивление источника тока и активное сопротивление катушки. Зная несколько сопротивлений R_i, включаемых в контур, можно определить величину R_к:

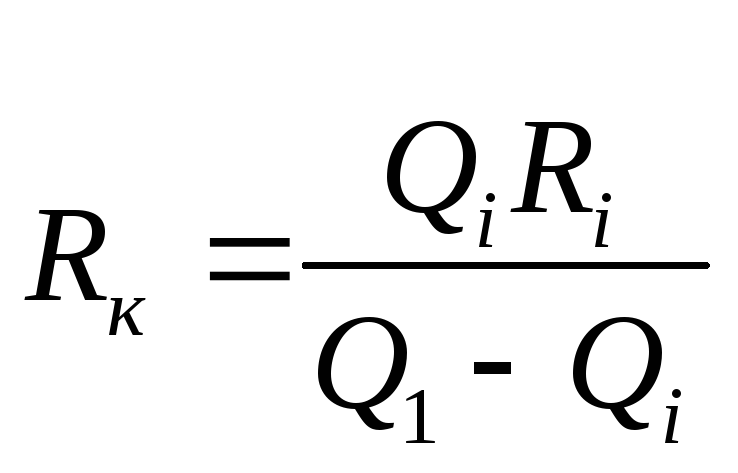. (10)

Если _о, резонансная частота _р_о и индуктивность контура может быть вычислена

L = 1/_o²C, _o_Ро=2_Ро. (11)

Зная величину индуктивности и сопротивление в контуре можно вычислить коэффициент затухания по соотношению

_i=(R_к + R_i)/2L. (12)

Порядок выполнения работы

1. Открыть диалоговое окно (щёлкнув дважды по «ярлык для резонанса» на рабочем столе), выбрать в меню «резонанс напряжения в RLC-контуре».

2. Установить значение емкости контура (по указанию преподавателя), занести значения С и _о в табл.1.

3. Получить изображения 4^х резонансных кривых, устанавливая значения R_м– 0, 100, 250, 500 Ом и активируя «мышкой» клавишу «строить».

4. Установить значение частот левой и правой границ в диапазоне примерно  10, 20 кГц от резонансной частоты, активируя режим масштабирования (кнопка с изображением увеличительного стекла). Занести значения U_c для 10 частот из диапазона масштабирования в табл.1.

5. Определить резонансные частоты _р, величины U_Cmax и занести в табл.1

6. Построить резонансные кривые U_c = U_c().

7. Вычислить величину добротности по формуле (8) и сопротивление контура R_к через добротности для различных сопротивлений R_м по (10). Результаты занести в табл.2

8. Вычислить индуктивность контура по резонансной частоте при Rм=0 и емкости конденсатора С (полагая  2o) по формуле (11).

9. Вычислить коэффициенты затухания _i по соотношению (12), записать результаты в табл.2 и сравнить со значениями резонансных частот _рез.

10. Сделать вывод о степени затухания колебаний в контуре.

Таблица 1.

	о=				С =
	Rм=0 Ом		Rм=100 Ом		Rм=250 Ом		Rм=500 Ом
	, кГц	Uc, В	, кГц	Uc, В	, кГц	Uc, В	, кГц	Uc, В
1
. . .
10
рез, кГц
Ucmax, В

Таблица 2.

Rм, Ом	Qi	RКi, Ом	Rк, Ом	DRк, Ом	, %	i	резi, с-1
0
100
250
500

Контрольные вопросы

1. Вынужденные колебания в контуре RLC-контуре, их возникновение, дифференциальное уравнение этих колебаний и его решение. Частота вынужденных колебаний.

2. Понятие электрического резонанса. Резонанс напряжения в контуре. Резонансная частота.

3. Добротность колебательного контура и определение добротности в данной работе.

4. Определение индуктивности контура в лабораторной работе. Определение сопротивления контура в лабораторной работе.

5. Определение контура коэффициента затухания в лабораторной работе.