Пз 1, 2, 3, 4. 4. Зразки розв’язування задач

4.1 . Побудова математичної моделі стохастичного експерименту.

Приклад 1. Експеримент – гральний кубик, на гранях якого вибито очки від 1 до 6, кидають один раз. Простір елементарних подій – множина чисел {1, 2, 3, 4, 5, 6}.

Приклад 2. Експеримент – гральний кубик, кидають два рази або кидають два гральні кубики. Простір елементарних подій множина чисел {1, 2, 3, 4, 5, 6} у другому – множина двозначних чисел { 11, 12, ... , 16, 21, 22, ... , 26, … , 61, 62, ... , 66 } – усього 36 елементарних подій (або наслідків).

Приклад 3. Нехай простір елементарних подій деякого ймовірносного експерименту . Тоді, наприклад, підмножина є подія, яка складається з елементарних подій і настає, якщо настає якась одна з цих елементарних подій. Про події кажуть, що вони утворюють подію А або сприяють події А.

Приклад 4. Гральний кубик кидають один раз. Подія – вірогідна, подія – неможлива, подія – випадкова.

Вірогідну подію позначають буквою Ω, неможливу символом (пуста множина), випадкові події позначають великими буквами латинського алфавіту А, В, С, ... .

Гральну кісточку кидають один раз. Події , – несумісні, а події А і – сумісні.

4.2. Алгебра подій.

Приклад 5. Гральний кубик кидають один раз. Подія А – випадало парне число очок і подія – однакові.

Приклад 6. Експеримент – гральний кубик кидають один раз. Якщо , то .

Зазначимо, що подія А і несумісні і, що , , .(Е інший вид запису Ω)

Приклад 7. Експеримент – точку кидають на площину. Нехай подія А полягає у влученні точки в область А, подія В – у влученні точки в область В, тоді подія полягає у влученні точки в заштриховану область ( див. рис. 1.1. ).

Рисунок 1.1

Наведені рисунки називаються діаграмами Венна ( зліва для несумісних, справа для сумісних подій ).

Діаграми Венна для добутку двох несумісних і сумісних подій мають вигляд:

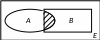
Рисунок 1.2

Для лівої діаграми .

Діаграми Венна для різниці двох несумісних і сумісних подій мають вигляд:

Е

Рисунок 1.3

Приклад 8. Події ( 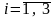), які полягають у влученні точки у відповідні області ( див. рис. 1.4 ), у сукупності несумісні, а парами сумісні.

Мають місце співвідношення ( закони або формули двоїстості де Моргана ):

і ,

або для n подій

і .

Рисунок 1.4

Довести ці рівності можна, наприклад, використовуючи таблиці, в яких перебрано всі можливі випадки настання (ненастання) задіяних у них подій. Так, для першої з них маємо

–	–	–	+	+	+	+
–	+	+	–	+	–	–
+	–	+	–	–	+	–
+	+	+	–	–	–	–

Тут «+» означає настання, «–» – ненастання події. Однаковість помічених стовпців і означає правильність рівності.

Приклад 9. Виконують один за одним три постріли з рушниці. Нехай ( ) – влучення в і – му пострілі. Необхідно складні події:

А – три влучення;

В – три промахи;

С – хоча б одне влучення,

виразити через елементарні події ( ).

Розв′язання:

– суміщення всіх трьох елементарних подій ( );

;

.

Приклад 10. Формула

D = C + A – C

еквівалентна формулі

,

де цифри задають порядок операцій над подіями.

Приклад 11. Спростити подію

Розв′язання.

.

Приклад 12. Зазначимо, що всі операції над подіями можна замінити лише двома операціями – заперечення і додавання, або заперечення і множення. Сказане випливає з формули де Моргана і співвідношень

і .

4.3. Комбінаторика.

Приклад 13. Маємо набір букв . З набору Е букву А можна вибрати 4 способами, В – 3 способами. Тому А або В можна вибрати способами, а впорядковану пару можна вибрати способами.

Приклад 14. Скільки тризначних чисел можна скласти з цифр 1, 2, 3, якщо кожна цифра входить у зображення числа лише один раз?

Розв’язання Кількість чисел

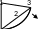
: 123, 231, 312, 132, 321, 213.

Приклад 15. Скільки двозначних чисел можна скласти з цифр 1,2,3, якщо кожна цифра входить у зображення числа лише один раз.

Розв’язання

.

Приклад 16. Скількома способами можна вибрати дві деталі з ящика, в якому три різні деталі (1, 2, 3)?

Розв’язання:

12, 23, 31 або 21, 32, 13

– тут вважається, що наслідками випробування є множина двозначних чисел.

Приклад Скільки чотиризначних чисел можна скласти з цифр {1, 1, 2, 2}?

Розв’язання:

– відрізняються одна від одної лише порядком елементів

Скільки двозначних чисел можна скласти з цифр 1, 2, 3?

Розв’язання Згідно із умовою задачі двозначні числа складаємо з цифр {1, 1, 2, 2, 3, 3} або з цифр {1, 1, … , 1, 2, 2, … , 2, 3, 3, … , 3}.

– відрізняються одна від одної або складом, або порядком елементів.

Приклад Скількома способами можна вибрати дві деталі з ящика, в якому три типи деталей?

Розв’язання Згідно із умови задачі в ящику l деталей типу 1; l деталей типу 2 і l деталей типу 3, . Вважаємо, що наслідками випробування є двозначні числа:

або

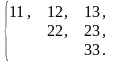
– відрізняються одна від одної лише складом елементів.

Приклад Скількома способами можна скласти трикутник:

1. З чотирьох відрізків з довжинами 4, 5, 6, 7 см?

2. З чотирьох типів відрізків з довжинами 4, 5, 6, 7 см?

Розв’язання:

1. .

2. .

Практичне заняття 5

КЛАСИЧНИЙ, СТАТИСТИЧНИЙ ТА ГЕОМЕТРИЧНИЙ ОЗНАЧЕННЯ ЙМОВІРНОСТЕЙ