Теорія ймовірностей

Практичні заняття 1, 2, 3, 4

ВИПАДКОВІ ПОДІЇ. АЛГЕБРА ПОДІЙ. ФОРМУЛИ КОМБІНАТОРИКИ

Теоретична довідка

Явища, перебіг яких при неодноразовому відтворенні одного і того ж досліду (експерименту) передбачити неможливо, називають випадковими. Та якщо провести велику кількість спостережень за випадковим явищем в одних і тих самих умовах, то можна помітити деякі закономірності.

Теорія ймовірностей – це математична наука, що вивчає об’єктивні закономірності масових випадкових явищ. Вона, як і будь-яка інша наука, виникла з практичної життєвої необхідності і є, на наш погляд, найбільш «експериментальною» з усіх математичних наук.

Мовою теорії експерименту є, безумовно, мова математичної статистики – математичної науки, яка вивчає методи збору та обробки результатів спостережень випадкових явищ для визначення їхніх закономірностей і характеристик.

Математична статистика, що опирається у своєму апараті на теорію ймовірностей, виникла і розвивалась паралельно з останньою. Предмет дослідження цих наук – випадкові явища або, як правило, випадкові величини – кількісні ознаки явищ. Водночас вихідні положення кожної науки істотно відрізняються. Так в теорії ймовірностей імовірнісна модель явища є відомою, і мова йде про прогнозування на її основі поводження цього явища в експерименті. На відміну від цього в математичній статистиці вихідними є дані спостережень досліджуваного явища, а кінцевим результатом – побудова його імовірнісної моделі.

Пз 1, 2, 3, 4. 1. Випадкові події, простір подій

Випробуванням (або дослідом, експериментом) називають здійснення певного комплексу умов або дій, що можуть бути відтворені будь-яке число разів. Наприклад: а) однократне підкидання монети і фіксування грані, яка буде верхньою після падіння; б) підкидання грального кубика та фіксування числа очок, що випали; в) хімічний експеримент; г) випробування сортів сталі на здатність до глибокого відпускання за методом Еріксона; д) вибір випадкової точки на відрізку тощо.

Кожна подія, що може відбутися в результаті випробування і не розкладається на простіші, називається елементарною подією або елементарним виходом ω. Множину всіх елементарних виходів позначають Ω і називають простором елементарних подій, а самі елементарні події – точками цього простору.

Елементарні події взаємно виключають одна одну, і в результаті експерименту обов’язково відбувається одна з них.

Випадкова подія A (або просто подія) – результат випробування, який при реалізації даного комплексу умов може відбутися чи не відбутися. Прикладами подій можуть бути: а) A - поява цифри при підкиданні монети; б) B - випадання трьох очок на верхній грані грального кубика; в) C - вибір точки 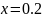, що належить відрізку .

Елементарні події, при яких дана подія A настає, називаються подіями, сприятливими цій події A. Таким чином, випадкова подія A визначається відповідним їй набором сприятливих елементарних подій і є підмножиною простору Ω (наприклад, ).

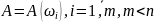Всякий мыслимый результат (неразложимый исход) эксперимента (испытания) будем называть элементарным случайным событием или элементарным событием, и обозначать .

Пр. 1 Монета подбрасывается два раза. Неразложимый исход эксперимента – возможные результаты двухкратного подбрасывания монеты (а не однократного, как может показаться на первый взгляд). Таким образом, неразложимый исход эксперимента зависит от условий поставленной задачи.

Пространством  элементарных событий будем называть совокупность элементарных событий , для которых

1. в результате реализации эксперимента всегда происходит одно из элементарных событий ;

2. все элементарные события  взаимно исключают друг друга.

Пространство элементарных событий считается заданным, если указаны все его элементы

или

.

Пр. 2 Монета подбрасывается два раза. Построить пространство элементарных событий.

Решение. Будем считать, что при однократном подбрасывании монеты возможно выпадение одной из ее сторон: либо «герб», либо «решетка» (ребро не учитываем). Рассмотрим всевозможные исходы реализации эксперимента, который состоит в подбрасывании монеты дважды:

₁ – выпадение «герба» два раза;

₂ – выпадение «герба» и «решетки»;

₃ - выпадение «решетки» и «герба»;

₄ – выпадение «решетки» два раза.

Других мыслимых результатов эксперимента нет. Таким образом, пространство элементарных событий состоит из четырех элементарных событий

.

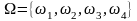Замечание. Почему события и следует считать различными? Искать логического объяснения, пожалуй, не стоит. Десятки и даже сотни тысяч экспериментов с монетой, да и не только с ней, показали, что в подавляющем большинстве случаев, если не оговорено противное, разумно учитывать порядок, в котором появляется то или иное событие.

Любое подмножество пространства элементарных событий будем называть случайным событием или просто событием и обозначать буквами A, B, C, … . Событие A происходит, если произошло какое – то одно из элементарных событий его составляющих.

Элементарные события, составляющие некоторое событие A, называются элементарными событиями, благоприятствующими появлению события A.

Пр. 3 Событие A состоит в появлении не более 3-х очков при однократном подбрасывании игральной кости. Построить пространство элементарных событий и описать событие A.

Решение. В данном случае, пространство элементарных событий состоит из 6 элементарных событий , где – выпадение i очков (числа i) при однократном подбрасывании игральной кости, 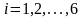. Поскольку появление не более 3-х очков при подбрасывании игральной кости равносильно появлению одной из 3-х граней кости с цифрами 1, 2 или 3, то будем считать, что событие A состоит из трех элементарных событий

.

Опр. Событие, которое всегда происходит, называется достоверным.

Достоверное событие содержит все элементарные события пространства . Пространство элементарных событий  является достоверным событием, поэтому часто для обозначения достоверного события используется символ .

Опр. Событие, которое никогда не происходит, называется невозможным.

Невозможное событие не содержит ни одного элементарного события из . Не нарушая общности, можно считать, что невозможное событие содержится в любом случайном событии. Аналогично обозначениям, принятым в теории множеств, для невозможного события принято использовать символ . Таким образом, для любого события A выполняется .

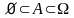Замечание. Строго говоря, достоверное и невозможное события не являются случайными, однако в теории вероятностей их рассматривают в целях конструктивности построения теории.

Пр. 4 Выпадение не более 6 очков при подбрасывании игральной кости – достоверное событие.

Пр. 5 Произведено 2 выстрела по мишени, при этом произошло 3 попадания – невозможное событие.

Для более отчетливого представления событий будем изображать (рис. 1) пространство элементарных событий  в виде некоторой области на плоскости. Элементарные события  - точками, а события A, B, C, … – областями внутри .

Опр. Событие A принадлежит событию B (рис. 2), если событие A состоит только из элементарных событий, принадлежащих событию B, и обозначается . Таким образом, появление событие A всегда за собой влечет появление события B.

Опр. События A и B называются равными (равносильными), если они состоят из одних и тех же элементарных событий, что записывается как 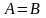(рис. 3).