4.2. Расчет фацетного параболоидного отражателя

При расчете фацетного параболоидного отражателя обычно ставят задачу получения наибольшей равномерности светового пучка. Поэтому оптический расчет отражателя ведут из условия равенства углов излучения всех зон отражения в меридиональной и сагиттальной плоскостях. При этом делают следующие допущения, упрощающие расчет [38]:

• угловые размеры каждой пластины характеризуются только угловым размером в одной меридиальной и одной сагиттальной плоскости;

• угловой размер источника света принимается одинаковым для всех точек данной пластины и равным угловому размеру по отношению в ее средней точке, характеризуемой углом φ с оптической осью отражателя.

Рис.4.10. Схема к расчету размеров и числа пластин отражателя

В меридиональном сечении отражателя, проходящем через среднюю точку пластины, фокальные лучи упадут на пластину в пределах угла Δφ (рис 4.10,а). Вследствие одинакового положения нормали N к поверхности в любой точке, отраженные фокальные лучи точек M_i-1 и M_i, образуют между собой угол Δα=Δφ. Таким образом, угол разворота фокальных лучей в меридиальной плоскости равен угловому размеру пластины в той же плоскости. Полный угол излучения пластины в меридиальном сечении будет

(4.8)

где - угловой размер источника света в меридиальной плоскости.

Для определения угла излучения в сагиттальной плоскости, перпендикулярной меридиальной и проходящей через среднюю точку пластины, необходимо найти угловые размеры светящегося тела и пластины в этой плоскости, содержащей радиус-вектор r (рис 4.10,б). Линейный размер пластины W в сагиттальном сечении определяется углом β между меридиальными плоскостями, совпадающими с ее боковыми кромками, и координатой Y средней точки. Зная линейный размер , можно найти угловой размер пластины в сагиттальном сечении:

, (4.9)

Полный угол излучения пластины в сагиттальной плоскости

, (4.10)

где - угловой размер источника света в сагиттальной плоскости.

Если выполнить условие равенства углов излучения всех зон заданному углу излучения параболоидного отражателя с фокусным расстоянием f, то при шаровом источнике света диаметром d для меридиональных плоскостей

и т.д. (4.11)

и для сагиттальных плоскостей

и т.д. (4.12)

Так как наряду с постоянством углов излучение всех зон отражателя требуется их постоянство для двух главных плоскостей одной пластины, можно написать

, (4.13)

где и - угловые размеры пластин i-й зоны в меридиональной и сагиттальной плоскости.

У источников света другой формы угловые размеры неодинаковы для меридиональной и сагиттальной плоскостей. Поэтому уравнения, аналогичные (4.13), будут выглядеть следующим образом:

для дискового источника диаметром d

; (4.14)

для нитевого источника длиной l и диаметром d

. (4.15)

Для этих и всех других круглосимметричных источников света можно написать равенства, аналогичные (4.11) и (4.12). При прямоугольном источнике света его угловые размеры в меридиональных сечениях разных пластин зоны различны. Для получения неизменного углового размера светового пучка от разных пластин одной и той же круговой зоны отражателя пришлось бы иметь пластины разного размера, что практически выполнить невозможно. Поэтому размеры прямоугольного источника света в двух главных плоскостях принимают одинаковыми и равными размерам квадрата, равновеликого по площади прямоугольному источнику света. При этом расчет углов излучения можно производить по формулам для дискового источника света, считая сторону квадрата равной d.

После расчета угловых размеров пластин в меридиональной и сагиттальной плоскостях определяют число зон и пластин в каждой круговой зоне отражателя.

При расчете параметров фацетного параболоидного отражателя необходимо решить вопрос о выборе фокусного расстояния f отражателя, которое определяется следующим выражением:

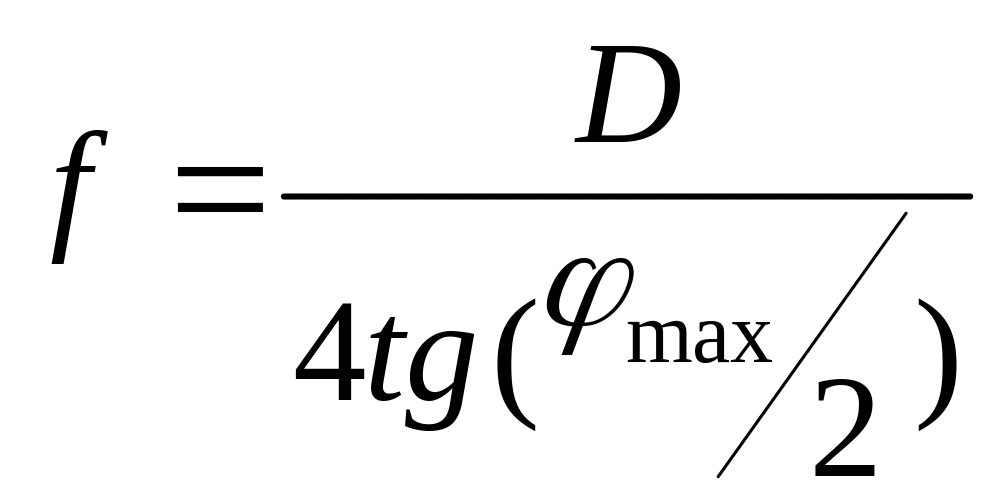, (4.16)

где D – диаметр отражателя;

φ_max- половина угла охвата отражателя.

Следовательно, естественно желание взять фокусное расстояние отражателя настолько малым, насколько позволяют размеры колбы применяемой лампы, для того чтобы получить при выбранном диаметре отражателя наибольший угол его охвата. Однако следует иметь ввиду, что расчет числа пластин отражателя производится из предположения, что передняя точка лицевой поверхности каждой пластины касается лицевого параболоидного остова, т.е. пластины расположены по касательной к данной точке остова. Такое расположение пластин практически не может быть выполнено, поэтому применяется другой способ расположения пластин – по хордам параболоидного остова. При этом каждая пластина имеет четыре точки с поверхностью остова, однако в этих точках нормали к пластине и остову имеют разные направления.

Следовательно, необходимо определить точку пластины, нормаль в которой совпадает с нормалью к остову отражателя, но эта точка уже не будет средней точкой пластины. Вследствие этого световой пучок пластины при установке светящегося тела в фокусе F отражателя окажется несимметричным относительно оптической оси и его однородность будет значительно ухудшена. Для получения от пластины светового пучка, симметричного относительно оптической оси отражателя, необходимо совместить светящееся тело с некоторым фокусом F₁, для которого f₁f. Таким образом, выбирая величину f параболоидного отражателя при известном диаметре колбы лампы, нужно учитывать необходимость приближения источника света к вершине отражателя из фокуса F в фокус F₁.

В работе [39] получена формула для определения зональных фокусных расстояний параболоида, удовлетворяющего условию симметричности светового пучка:

, (4.17)

Величина f₁ всего отражателя определяется как среднее из зональных фокусных расстояний:

. (4.18)

Для установки лампы в вершине отражателя часто делают отверстие. При этом следует учитывать, что уменьшение фокусного расстояния отражателя с целью увеличения его угла охвата будет сопровождаться увеличением центрального отверстия, диаметр которого выбирается исходя из размеров колбы лампы, а следовательно, и увеличением потерь светового потока в этом отверстии. Величина потерянного светового потока определяется не только величинами углов охвата отражателя φ_max и центрального отверстия φ₀, но и кривой распределения силы света применяемой лампы.

При выборе начала координат в вершине параболоидного отражателя, абсциссы плоскости центрального отверстия х₀ и светового диаметра отражателя х_max могут быть определены по следующим формулам [38]:

и , (4.19)

где r₀ и R- радиусы центрального и светового отверстия отражателя.

Расчет фацетного параболоидного отражателя можно выполнить, используя следующую методику [39]:

1. Задаемся диаметром отражателя D и его максимальным углом охвата 2φ_max. Определяем фокусное расстояние f отражателя:

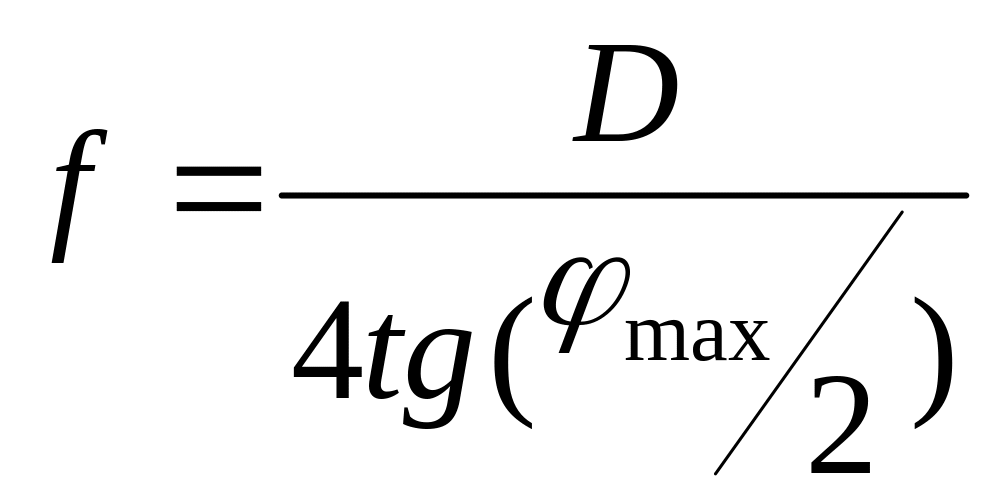
2. Выбираем лампу и определяем размеры источника света (например, для газоразрядных ламп длину l и диаметр d дуги разряда). Рассчитываем угловые размеры источника света в меридиональной и сагиттальной плоскостях:

, .

3. Задаемся допустимым углом излучения α_зад отражателя и определяем число круговых зон отражателя и их угловые размеры в следующей последовательности:

Расчет углового размера первой зоны. Для первой зоны берется одна круглая пластина (β=360⁰), и центр ее совмещается с вершиной отражателя (рис 4.11).

Рис.4.11. Вид светового отверстия параболоидного пластинчатого отражателя с шаровым светящимся телом

Следовательно, .

Расчет углового размера второй зоны. Задаемся некоторым значением углового размера второй зоны. Далее определяем угол:

.

Подставляем значение в уравнение (4.15) и, используя тригонометрическое преобразование

,

получим

Рассчитанный угол сравниваем со значением .

Подбор угла производится до тех пор, пока не будет удовлетворено неравенство

.

Расчет углового размера третьей из всех последующих зон. Задаемся значением углового размера третьей зоны и находим угол к ее средней точке

,

далее определяем угол

.

Подбор величин делается до тех пор, пока не будет удовлетворено неравенство

.

Для всех остальных зон углы и определяются по формулам

;

.

Расчет ведется до тех пор, пока сумма угловых размеров зон не будет равна углу охвата отражателя φ_max. Следовательно, общее число зон отражателя n определятся условием:

.

4. Определяем число пластин отражателя. Зная из предыдущего расчета для каждой зоны , для всех зон определяем угловые размеры источника света в сагиттальной плоскости ξ_s:

.

Далее, используя уравнение (4.10), рассчитываем угловой размер пластин каждой зоны:

.

Определив сагиттальный размер пластины, можно найти число пластин в каждой зоне:

и общее число пластин всего отражателя

.

Число пластин не должно быть дробным, что является критерием окончательного выбора величины .

5. Определяем зональные фокусные расстояния и величину фокусного расстояния всего отражателя:

;

.

6. Для отражателя с отверстием под лампу определяем координаты плоскостей центрального и светового диаметра:

и .

7. Определяем координаты Х и У профиля параболоидного отражателя.

.

В качестве примера выполним расчет фацетного параболоидного отражателя при следующих исходных данных:

- источником света служит ксеноновая лампа ХВО450W/2OFR мощностью 450 Вт. Диаметр колбы лампы D_л=29 мм, длина лампы L_л=117 мм, размеры дуги разряда lxd=2,7х0,9 мм.

- фацетный параболоидный отражатель, диаметром D=80 мм имеет максимальный угол охвата при .

Результаты расчета приведены в табл. 4.3 и на рис.4.12.

Таблица 4.3

Результаты расчета фацетного параболоидного отражателя

Зона	град.	град.	град.	град.	град.	град.	град.	град.	шт.	мм.
1	-8	8	0	12	20	8	4	360	1	20
2	8	26	15,5	18	20	2	4	60	6	14,9
3	26	42	31	16	20	4	2	35	10	18,1
4	42	58	48	16	20	5	2	24	15	19
5	58	73	62	15	20	5	2	20	18	19,3
6	73	88	77,5	15	20	4,5	1,5	18	20	19,4
										f1=18,5

Рис. 4.12. Результаты габаритного расчета фацетного параболического отражателя