3.5.3. Пример габаритного расчета диоптрической (линзовой) светооптической системы lcd-видеопроектора

Оптическая система осветителя состоит из конденсора и дополнительного зеркального отражателя, изображающих источник света во входной зрачок проекционного объектива (рис. 3.15).

В качестве примера выполним габаритный расчет светооптической системы LCD-видеопроектора при следующих исходных данных:

• формат ЖК-матрицы 1.3″ (диагональ l_м=33 мм);

• размер экрана 3х2 м² (диагональ L_э=3,6 м);

• освещенность экрана E=100 лк;

• расстояние до экрана P′=10 м.

Рис. 3.15. Схема для расчета диоптрической светооптической системы LCD-видеопроектора

Источником света служит галогенная лампа OSRAM 93723 со следующими характеристиками:

• мощность W=1200 Вт;

• напряжение питания V=80 В;

• световой поток Ф=37500 лм;

• габаритная яркость В=37 10⁶ кд/м²;

• размеры тела накала схb=12,7х12,7 мм²;

• диаметр колбы Dл=22,2 мм;

• длина лампы l_л=120,7 мм;

Использование дополнительного зеркального отражателя позволяет увеличить габаритную яркость лампы примерно на 25% т.е.

.

Определим оптические характеристики проекцион-ного объектива. Из заданных размеров ЖК-матрицы и экрана находим линейное увеличение объектива

.

Фокусное расстояние объектива определим из формулы (3.35)

Из выражения (3.26) находим диаметр выходного зрачка объектива, предварительно полагая, что общий коэффициент пропускания светооптической системы видеопроектора τ = 0,2:

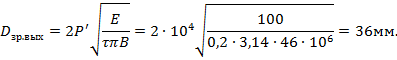
Диаметр входного зрачка объектива определяется формулой (3.27) и при линейном увеличении в зрачках объектива β₀=1 равен

Относительное отверстие объектива будет равно

Расстояние х от переднего фокуса объектива до ЖК-матрицы согласно формуле (3.37) составит

Так как ЖК-матрица расположена вблизи передней фокальной плоскости объектива, то его поле зрения со стороны ЖК-матрицы определяется выражением (3.28):

Для расчета конденсора определим его линейное увеличение β_К из условия, что изображение светящегося тела лампы заполняет весь входной зрачок проекционного объектива. Светящаяся площадка имеет размеры следовательно, увеличение конденсора согласно формуле (3.21) будет равно

Угол охвата конденсора 2ω₀ определим из выражения (3.33)

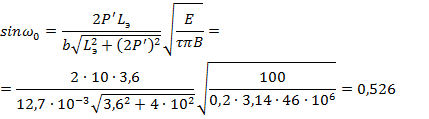
Следовательно, ω₀=30° и 2 ω₀=60°.

Таким образом, конденсор должен иметь следующие параметры:

В проекционных системах применяют различные типы конденсоров. Количество и форма линз конденсора выбирается исходя из требуемого увеличения и угла охвата осветительной системы [10, 11, 29].

Однолинзовый конденсор (рис. 3.16) применяется при углах охвата 2 U₀≤25⁰, увеличении и представляет собой, как правило, двояковыпуклую линзу с равными по абсолютной величине радиусами. Если однолинзовый конденсор используется при других увеличениях, то его форму определяют из условия получения наименьшей сферической аберрации.

Рис. 3.16. Однолинзовый конденсор

Двухлинзовый конденсор имеет угол охвата 2 U₀=50– 60⁰. Конденсор, состояший из двух одинаковых плоско-выпуклых линз (рис. 3.17, а), может иметь линейное увеличение . В конденсоре, у которого обе линзы рассчитаны на минимум сферических аберраций, первая линза является апланатической, а вторая двояковыпуклой (рис. 3.17, б). В этом случае линейное увеличение может быть увеличено до .

а) б)

Рис. 3.17. Двухлинзовый конденсор

Трехлинзовый конденсор (рис. 3.18, а) обеспечивает угол охвата Максимальное линейное увеличение таких конденсоров составляет .

Четырехлинзовый конденсор (рис. 3.18, б) обеспечивает угол охвата с линейным увеличением до .

Следует отметить, что применение в конденсорах линз с асферическими поверхностями или линз Френеля позволяет увеличить угол охвата до 110°.

а) б)

Рис. 3.18. Трех- и четырехлинзовый конденсоры

В нашем случае при можно использовать двухлинзовый конденсор. Так как плоско-выпуклая линза имеет наименьшую сферическую аберрацию при бесконечном (достаточно большом) удалении от изображения, то, очевидно, оптимальным будет конденсор из двух одинаковых плоско-выпуклых линз (рис. 3.17, а).

Для такого конденсора, если сферические поверхности линз соприкасаются, его оптическая сила – оптические силы первой и второй линзы конденсора. При одинаковых линзах Следовательно

– фокусные расстояния линз конденсора. Такие конденсоры используются при . Однако если , то принимают .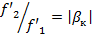

Для того чтобы дефекты конденсора не изображались резко на экране, выберем расстояние e между конденсором и ЖК-матрицей, равное e =10мм (рис. 3.15).

Расстояние определим из рис. 3.15 при и , где – толщина линз конденсора. Расстояние между линзами .

Тогда положение источника света и фокусное расстояние конденсора в соответствии с формулами (3.39) и (3.40) будут равны

Фокусные расстояния линз конденсора с учетом того, что и , будут равны

Габаритный расчет конденсора можно выполнить, используя метод вспомогательного луча. Пусть вспомогательный луч, идущий из центра светового тела О, (рис. 3.15), имеет такое направление, что при выходе из конденсора он проходит через точку М ЖК-матрицы и пересекает оптическую ось в центре О’ входного зрачка объектива. Углы этого луча с оптической осью обозначим через α_к, а высоты – через h_к. При этом α₁=ω₀ и α₅=ω.

Радиусы кривизны линз конденсора r_к связаны с параметрами вспомогательного луча следующими формулами [29]:

(3.54)

. (3.55)

Пусть обе линзы сделаны из стекла с показателем преломления n=1,5. Толщины линз d₁=d₃=6 мм, а расстояние между ними d₂=0. Если в дальнейшем окажется, что эти толщины выбраны неудачно, следует выбрать новые данные и сделать перерасчет.

Для начала расчета имеем следующие данные (рис. 3.15):

n₁=1; n₂=1,5; n₃=1; n₄=1,5; n₅=1;

d₁=6мм; d₂=0; d₃=6мм;

; х=-0,83мм; e=10мм;

.

Величину h₄ можно определить из рис. 3.15

.

Параметры α₂, α₃, и α₄ могут быть различной величины и зависят от формы линз конденсора. Для конденсора, состоящего из двух плоско-выпуклых линз, соприкасающихся сферическими поверхностями (рис. 3.15), на основании выражения (3.54) можно записать следующие дополнительные условия :

1. ;

2. 

3. .

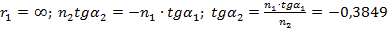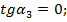
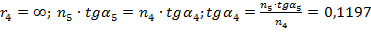Теперь из формулы (3.55) можно определить все высоты h_k:

;

;

.

Для расчета радиусов кривизны линз конденсора воспользуемся формулой (3.54)

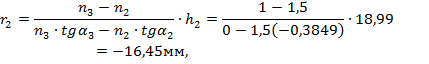
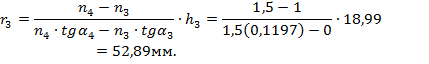
Таким образом, имеем следующие радиусы кривизны линз конденсора:

При определении диаметров линз конденсора надо рассчитать (в обратном ходе) направление действительного луча, идущего из нижнего края А΄ входного зрачка объектива через точку М ЖК-матрицы и приходящего в точку А источника света (рис. 3.15).

Угол φ между лучом A΄M и линией, параллельной оптической оси, можно определить из выражения

Световой диаметр второй линзы конденсора будет равен (рис. 3.15)

Полный диаметр этой линзы с учетом припуска на оправу Δ=2мм составит

Так как высота h₁=16,68мм вспомогательного луча на входе первой линзы конденсора меньше высоты h₄=18,28мм на выходе второй линзы можно принять диаметр первой линзы D₁=D₂=42,5мм.

Следует отметить, что найденные конструктивные параметры конденсора являются первым приближением и дают лишь представление о его виде. Окончательные параметры конденсора и положение источника света находятся в результате аберрационного расчета [11].

Зеркальный сферический отражатель (рис. 3.15) позволяет более полно использовать световой поток источника света и должен быть установлен так, чтобы источник света находился в центре кривизны зеркала.

Для расчета зеркального сферического отражателя (рис 3.19) имеем следующие исходные данные :

• угол охвата отражателя

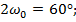
• диаметр колбы лампы

• расстояние от колбы лампы до отражателя

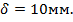
Радиус отражателя R_от будет равен

Диаметр отражателя D_от в пределах угла охвата можно определить по формуле

Глубину отражателя Г_от определим из выражения

Рис. 3.19. Схема расчета зеркального сферического отражателя

Полученные результаты габаритного расчета светооптической системы, показанной на рис. 3.15, представлены на рис. 3.20.

Рис. 3.20. Результаты габаритного расчета светооптической системы

В качестве проекционного объектива можно выбрать объектив LNS-T50 фирмы Sanyo, имеющий следующие параметры [22]: f=59-107мм; ɛ=1:(2,0-2,9).