Свойства непрерывной функции на отрезке, Типы точек разрыва

Если ф-ция f(x) непрерывна в каждой точке отрезка АВ, то говорят она непрерывна на этом отрезке. Ф-ция непрерывная на АВ обладает следующими св-ми:

1.Если ф-ция f(x) непрерывна на АВ, то внутри этого отрезка найдётся такое значение x, хотя-бы одно при котором ф-ция принимает наименьшее или наибольшее значение.

2.Если ф-ция f(x) непрерывна на интервале АВ, принимает некоторое значение М и m, а значение m<k<M, то найдётся такое x на интервале АВ, что f(x)=k

Точки разрыва ф-ции. Если ф-ция f(x) разрывна в точке x₀, то точку x₀ называют точкой разрыва f(x).

Точки разрыва определяют по следующим типам:

1.Точки устранимого разрыва – это такие точки в которых ф-ция не существует, а левый и правый пределы равны в этой точке. (Пример: I замечательный предел). Чтобы устранить разрыв нужно доопределить ф-цию в этой точке.

Точки разрыва первого типа: такие точки в которых левые и правые пределы конечны и неравны между собой. Этот разрыв называют – разрыв типа скачка.

Точки разрыва второго типа – когда левый или правый или оба – бесконечны.

Свойства непрерывной функции на отрезке,

Типы точек разрыва

Непрерывность функции в точке.

Свойства непрерывной функции.

пределов этих функций.) можем записать предел частного. На основании определения непрерывности ф-ции является непрерывной.

Если имеем сложную ф-цию образованную суперпозицией некоторых других ф-ций

Если образующие сложную ф-цию образующих x₀, то сложная ф-ция непрерывна в этой точке.

Если f(x)>0 и непрерывна в точке x₀ и ф-ция g(x) непрерывна в точке x₀, то степенно-показательная ф-ция непрерывна в этой точке.

Связь бесконечно малых функций,

сравнение их

Понятие производной.

Геометрический и физический смысл

Возьмём отношение y и x при x0 и y0, но в отношении эти две бесконечно малые величины y и x могут иметь любое значение. Тогда имеет смысл рассмотреть предел этого отношения при x0

Выражение (1) показывает какая из величин x и y стремиться к нулю быстрее. И если этот предел конечен, то соотношение (1) называют производной ф-ции, и обозначают или.

В механическом смысле – производная представляет следующее: пусть некоторая точка М движеться по некоторой траектории S(t) в некоторый момент (t) точка М находится в А

(S(t)A, через некоторое время t точка М перейдёт в точку S(t+t)- S(t)0

Средняя скорость движения точки недостаточно характеризует движение т.е. на каких-то участках скорость меньше средней, а на других больше. Чтобы получить скорость в каждый момент времени т.е. мгновенную скорость, нужно уменьшать t и перейти к пределу при t0;

Производная – мгновенная скорость движения точки по своей траектории.

Правило дифференцирования (Суммы, производной, частного ф-ций)

Если имеем две функции U(x) и V(x), которые имеют производные в точке x₀ т.е. U`(x) и V`(x), то производные суммы произведения, частного этих функций соответственно равны:

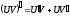
Доказательство:

U+V=(x)

xx +x; (x)(x+x)-(x)=U(x+x)+V(x+x)-

-U(x)-V(x)