
Дифф-е ф-ий мног. Перемен. Частные произв. 1 и высш. Пор.
Для ф–ии мног. перем. гов. о частной произв. по какой-либо перемен.
дано: u=f(x1,x2…xn)
частич. прир. по перем. xi:
Δxif=f(x1, x2…xi-1, xi+Δxi, xi+1…xn)-f(x1, x2…xi…xn)
опр.:
частной произв. по перемен. xi
наз.:
![]()
обозн.: uxi’=∂u/∂xi
оконч-но:
![]()
Прав., извест. для ф-ий 1 перем. вып. и здесь. Прав. нахожд. частн. произв. по какой-то перемен. те же, что и для ф-ий 1 перем., в предполож., что все остальн. перемен. явл. константами.
Поск-ку част. произв. 1 пор. - ф-ии нес-ких перем., опред. в какой-то обл., то их также можно диф-вать. Произв. от 1 произв – произв 2 пор.
дано: u=f(x1..xn)
∂u/∂x1=1(x1, x2…xn) ∂u/∂x2=2(x1, x2…xn)…∂u/∂xn=n(x1, x2…xn)
![]()
Теор.:
![]()
![]()
iо
произв. от произв 2 пор. – произв. 3 пор. и т.д.
для ф-ии 2 перемен.: z=f(x,y)





 zx’
zy’
zx’
zy’
zxx’’ zxy’’ zyx’’ zyy’’
Теор.: (о
рав-ве смеш. произв.) если z=f(x,y)
непрер-но диф-ма вместе со своими частн.
произв. до 2 пор. включ-но, то смеш.
производные равны друг другу.
![]()
зам.: при вып. соотв. условий теор. верна для частн. произв. более выс. порядка.
зам.: при выполн. соотв. условий теорема о рав-ве смеш. произв. вып. для ф-ий больш. кол-ва переменных, чем 2.
z=f(x,y)


zx’ zy’
zxx’’, zxy’’, zyy’’
zxxx’’’, zxxy’’’, zxyy’’’, zyyy’’’
Дифференциалы 1 порядка.
Для ф-ии 1 перемен. диф-ал 1 пор. – гл. часть приращ.
Ф-ия 2 пермен. наз. дифф-мой в т. (x,y) если ее приращ. представимо в виде: Δz=(fx’(x,y)+α1)Δx+(fy’(x,y)+α2)Δy=fx’(x,y)Δx+fy’(x,y)Δy+(α1Δx+α2Δy)
обозн.:
![]()
Диф-ал ф-ии 2 перемен. зав. от 4 пермен.: x,y,Δx,Δy
если z=x, то dz=dx=Δx, если z=y, то dy=Δy и : dz=fx’(x,y)dx+fy’(x,y)dy
СВОЙСТВА:
1) d(z1(x,y)±z2(x,y))=dz1(x,y)±dz2(x,y)
2) d(z1·z2)=z2·dz1+z1·dz2
3) d(z1/z2)= z2·dz1-+z1·dz2/z22
4) св-во инвариантн-ти: df(x)=f’(x)dx
В приближ. вычисл.: f(x+Δx,y+Δy)≈f(x,y)+dz(x,y,Δx,Δy)
Дифф-алы высш. пор. для ф-ий мног. перемен.
Диф-ал 2 пор. – это диф-ал от 1 пор. d2z=d(dz)
dnz=d(dn-1z)
Для z=f(x,y) где x и y – назавис. пермен.:

d2z=zxx’’(dx)2+2zxy’’dxdy+zyy’’(dy)2
Для упрощ. написан. ф-л диф-лов высш. пор. польз. оператором:
![]()
С пом. него можно написать:

Прим. ф-лу бинома Ньютона можно найти ф-лу для n-ого диф-ла:
для ф-ии z=f(x1,x2…xn):
![]()
замеч.: если для ф-ии z=f(x,y) x=x(u,v) то уже для 2 диф-ла y=y(u,v) св-во инвар. отсутствует.
|
Табл. осн. неопред. интегр. 1)
2)
3)
4)
5)
6)
7)
8)
8~)
9)
10) «длинный логарифм»:
11) «высокий логарифм»:
12)
13) 14) 15)
|
Напр. И градиентом.
Говор., что в т. М(x,y)DR2 зад. скал. поле если u=u(x,y)
Хар. скал. поля – линии уровня u(x,y)=c Если т. М(x,y,z)DR3
u=u(x,y,z) u(x,y,z)=с – пов-ть уров.
дано: т. M(x,y,z) т.M1(x+Δx,y+Δy,z+Δz)
![]()
![]()
опр.:
произв. по напр.
![]() назыв.:
назыв.:

обозн.: ∂U/∂S

исх. из опр. ясно что произв. по напр. дает скор. измен. поля в дан. напр.
из опр.:
![]()
для плоск. поля:
![]()
Градиент
скал. поля U=U(x,y,z)
![]()
направление градиента:
1) для плоск. случ.:
U=U(x,y)
![]()
Град. напр. по нормали к лин. уров. U(x,y)=с
Угл. коэф. кас., норм.: k1=y’(x)=-U’x/U’y k2=-1/k1=U’y/U’x
опр.: каст. пл-тью к пов-ти S F(x,y,z)=0 в т.M0(x0,y0,z0) S наз. пл-ть содерж. все каст. прямые, провед. к люб. лин, лежащим на пов-ти S и прох. через т.M0
Нормаль – перпенд. к касат. пл-ти в дан. т.
Ур-е кас. пл-ти:
![]()
Ур-е норм.:

в папр. град. произ. по напр. максим.
1) (x)’=x-1 степ. ф-ия
2) (ax)’=axlna a>0 a1 показ. ф-ия
(ex)’=ex
3) (logax)’=1/xlna a>0 a1
(lnx)’=1/x логар. ф-ия
4) (sinx)’=cosx тригон. ф-ии
(cosx)’=-sinx
(tgx)’=1/cos2x
(ctgx)’=-1/sin2x
5)
(arcsinx)’=1/![]() обрат.тр.ф.
обрат.тр.ф.
(arccosx)’=-1/![]()
(arctgx)’=1/1+x2
(arcctgx)’=-1/1+x2
6) (chx)’=shx
(shx)’=chx
(thx)’=1/ch2x
(cthx)’=-1/sh2x


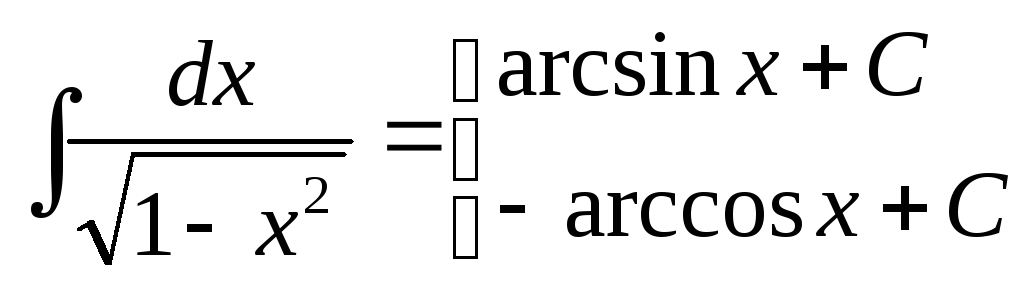
 a0
a0