3. Модель державного боргу

Співавтор: Коруна Світлана Миколаївна

Розглядаючи основні параметри державного боргу як стохастичні процеси, побудовано модель шляхом встановлення прогнозного значення їхніх законів розподілу з подальшим відтворенням випадкових послідовностей, що підлягає цим законам розподілу.

Поставлено задачу [⁷] побудувати модель зміни з часом державного боргу з урахуванням особливостей його реструктуризації на банківському та фондовому ринках. Розв’язання цієї задачі веде до створення засобів дослідження державного боргу України, що дозволить створювати ефективні плани його реструктуризації та погашення [⁸].

Утворення боргу та його погашення – це особливі фінансові операції, в яких відбуваються трансакції з від’ємною кількістю грошей. У всіх інших відношеннях, крім цього «арифметичного знаку» суми переказу, операції з боргом не відрізняються від інших фінансових операцій, зокрема – від операцій на фондовому рику. Взагалі, операції з борговими зобов’язаннями власне становлять невіддільну частину інших операцій на фондовому рику, таких як операції з цінними паперами, торгівля опціонами тощо, укладання ф’ючерсних контрактів. Тому для моделювання державного боргу доцільно застосувати математичний апарат, який використовують, описуючи фінансові операцій – методи так званої фінансової математики.

Зауважимо, що перші спроби описати фінансові операції, зокрема – операції з боргами були зроблені ще 1900 р. французьким математиком М.Башельє [⁹]. На основі цієї роботи П.Самуельсон розробив формулу, добре відому серед економістів [¹⁰], яка задає значення ціни опціону від часу

(3.1)

де S(t) – ціна акції в момент часу t; S₀ – ціна акції в момент часу t = 0; μ – коефіцієнт тренду, який відображає середню зміну швидкості ціни акції; σ – коефіцієнт волатильності, який відображає міру коливання доходності фінансових елементів – акцій, опціонів, ф’ючерсів, боргових трансакцій тощо; W(t) – стохастичний процес з нульовим математичним сподіванням. Чим вища волатильність активів й пасивів, тим більша їх ризиковість.

Як з’ясувалося [¹¹], залежність (1.2) є частинним випадком розв’язку так званого рівняння Блека-Шоулса:

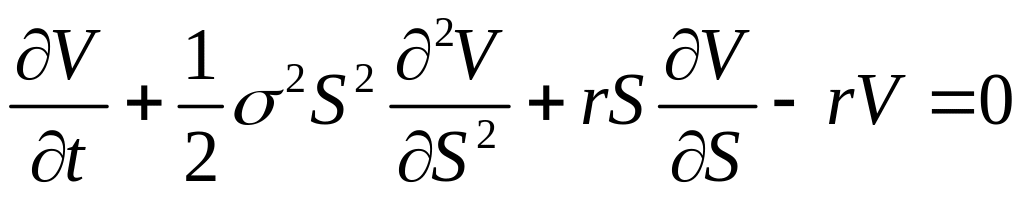, (3.2)

де r – процентна ставка без ризикової трансакції з пасивами або активами, V абсолютне значення різниці між вартістю опціону S і його ціною K у момент виконання T.

Рівняння (3.2) має явний розв’язок:

, (3.3)

, (3.4)

, (3.5)

де Φ(x) – характеристична функція нормального розподілу.

Складність практичного застосування рівнянь (3.3) – (3.4) для моделювання вартості кол-опціонів та пут-опціонів пов’язана з тим, що вони виведені на припущенні про відоме значення волатильності σ. В дійсності ж її значення невідоме і практичне визначення волатильності за експериментальними даними становить одну з головних проблем сучасних фінансів.

На практиці використовують два методи визначення волатильності. Перший з них полягає у підставлянні в ліву частину рівняння (3.3) вартості реально проведеного опціону, в праву частину – моменту T його проведення і розв’язування цього рівняння відносно σ.

При другому підході волатильність визначають за масивами реальних даних. Але при цьому виникає проблема розв’язування ідентифікаційних рівнянь, некоректних в сенсі Адамара. Практично ж для оцінки волатильності використовують ряд емпіричних формул, які ґрунтується на різних статистичних оцінках спостережуваних вибірок реальних даних.

Волатильність як середньоквадратичне відхилення:

, (3.6)

де r(t) – індексна дохідність, визначена як логарифм відношення ціни закриття опціону за біжучий та попередні дні:

, i=2,…,n, (3.7)

де – середня дохідність на [t₁, t_n].

Волатильність за Паркінсоном [¹²] вираховується через найбільше і найменше значення ціни під час проведення опціону:

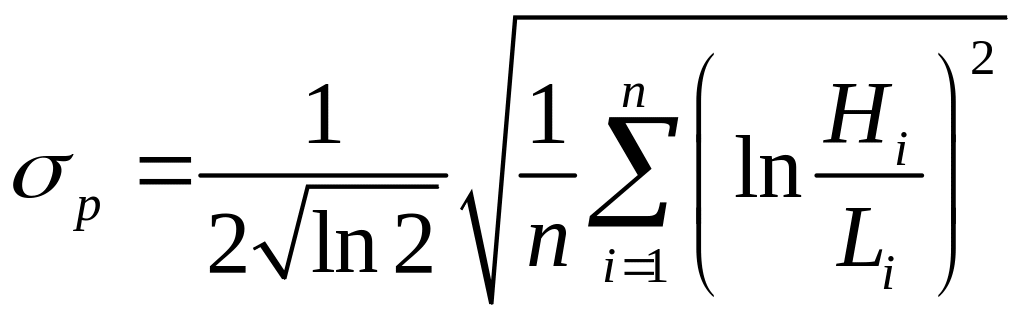, (3.8)

де H_i, L_i – відповідно найбільша і найменша вартість опціону протягом i-того дня.

Гарманом і Класом [¹³] запропоновано визначати волатильність за співвідношенням між ціною Q(t_i) відкриття і ціною закриття С(t_i) опціону.

. (3.9)

Методи вирахування волатильності за експериментальними даними дозволяють практично розв’язати частину задачі моделювання боргу, але в них не враховано двох особливостей, пов’язаних з торгівлею пасивами. По-перше, під час продажу торгових зобов’язань відбувається зміна не лише волатильності, а й численних інших параметрів цього стохастичного процесу. Які також необхідно враховувати, обчисляючи величину боргу.

По-друге, урахування випадкових величин в праві стороні диференційного рівняння приводить до рівнянь типу Коломогорова, які практично важко розв’язувати з допомогою числових методів. Тому побудова моделі на основі рівняння (3.2) або його аналогів веде до суттєвих трудностей під час пізніших обчислень з моделлю.

Ще одна особливість поставленої задачі полягає не просто у торгівлі пасивами, а у перехід державних боргових пасивів у систему фінансових трансакцій на фондовому ринку, тобто у перетворенні «нерухомих, заморожених» боргів у борги, які є фінансовою основою звичайних трансакцій з пасивами. Тобто йдеться про особливу фінансову дію – монетаризацію боргу, його перехід з поняття юридичного майнового зобов’язання у поняття опціонних торгів пасивами. Тобто, термін «монетиризація державного боргу» передбачає грошові виплати купонів і номіналу, іншими словами, повне повернення боржником, «відповідно до умов контракту», раніше отриманих ним засобів [¹⁴]. Вужче цей термін характеризує участь національного банку в покупці державних боргових зобов'язань на вільному ринку. Монетиризація заміщає урядові борги на «дзвінку монету» за виразом Рікардо, на борги банку в сучасному виді. Таким чином, магнетизація боргу — це загальний процес взаємодії грошей і боргів, що особливо повно виявляється у фінансуванні дефіциту державного бюджету [¹⁵].

Тому поставлена задача моделювання величини боргу зводиться до задачі імітування нестаціонарного стохастичного процесу, який з часом змінює свій закон розподілу та інші параметри.

Нижче подано математичний опис розв’язання цієї задачі.

Під монетаризацією боргу розумітимемо два процеси – стохастичний процес u(t) виникнення зобов’язань, і стохастичний процес погашення зобов’язань y(t), або їх зникнення у зв’язку з поверненням коштів позичальником кредиторові.

Явища надмірно великого боргу так і надто інтенсивного його погашення є несприятливими для економіки, тому шукана модель має інструмент для пошуку ефективних темпів виникнення та погашення заборгованості.

Природно припустити, що швидкість виникнення боргу є нелінійною функцією його величини і залежить від адитивної випадкової величини:

(3.9)

Останнє рівняння еквівалентне рівнянню Фокера-Планка-Колмогорова і його стаціонарний розв’язок має вид:

, (3.10)

де величини V(u) – так званий потенціал і G – параметр, який називають коефіцієнтом дифузії встановлюється на основі функції F(u), якщо вона відома. Проте, в поставленій задачі ця функція невідома, тому залишається шукати розподіл (3.10) за експериментальними даними.

Зауважимо, що розподіл (3.10) описує густину ймовірності операції виникнення боргу, й аналогічний невідомий розподіл

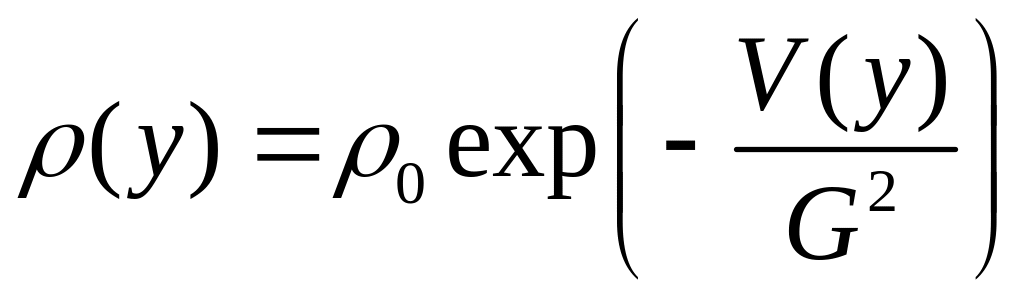(3.11)

описує густину ймовірності операції його погашення. Невідомі шукані розподіли (3.10), (3.11) суттєво залежать від часу.

Додамо, що рівняння (3.9) співпадає з рівнянням фінансування бюджетного дефіциту [¹⁶].

Поставлена задача зводиться до ідентифікації параметрів

сu(t), c_y(t) (3.12)

розподілів

, (3.13)

за відомими експериментальними даними про обсяги операцій виникнення u(t) та погашення y(t) боргу:

u(t_k), y(t_k), k=1,…,m. (3.14)

Розв’язання поставленої задачі зводиться до двох послідовних під задач – вибору структури алгебричного виразу розподілів (3.13) та ідентифікації їх параметрів (3.12) за експериментальними даними (3.14).

Спочатку обґрунтуємо вибір структури. Оскільки модельоване явище описує рівняння Фокера-Планка-Колмогорова виду (3.9), тому структуру шуканого розподілу доцільно вибрати у формі експоненційного розподілу

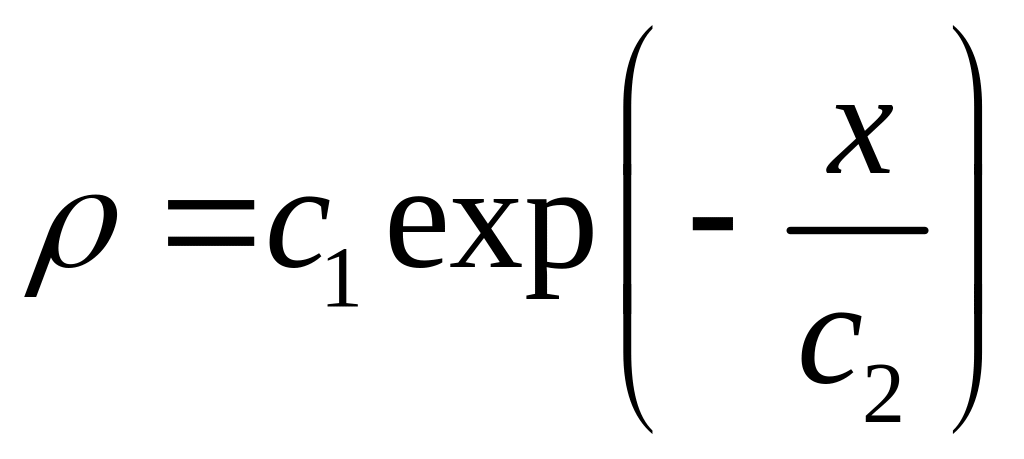(3.15)

або розподілу Парето

(3.16)

В обох випадках задача параметричної ідентифікації моделі зводиться до розв’язування системи нелінійних алгебричних рівнянь.

Дальше опишемо алгоритм розв’язання поставленої задачі.

Позначимо для простоти ідентифікатором x – обидві модельовані величини u, y.

Виберемо з множини експериментальних даних (3.14) першу підмножину суміжних елементів

, (3.16)

яка містить крайні ліві значення послідовності (3.14). Тоді вдруге виберемо підмножину суміжних елементів (3.14), які розміщені правіше, тобто відповідають пізнішим моментам часу і створимо другу підмножину X2, яка своїми елементами частково перекривається з першою множиною. Аналогічно створимо n ковзних множин,

, (3.17)

що охоплюють m суміжних елементів, які частково перекриваються між сусідніми ковзними підмножинами. Середина відрізку часу ковзної множини

(3.18)

відображає приблизне значення часу, з яким зіставлена ковзна вибірка X_j нестаціонарного стохастичного процесу (3.14).

Для кожної з ковзних вибірок (3.17) з допомогою числових методів легко встановити дискретне значення закону розподілу

. (3.19)

Допустимо, що з розв’язку нелінійного алгебричного рівняння

(3.20)

визначено коефіцієнти нелінійної апроксимації c_j дискретно заданого закону розподілу (3.19) з допомогою алгебричного співвідношення виду (3.15)-(3.16) для всіх ковзних вибірок X_j j=1,…,n. В результаті цього отримано дискретну послідовність зміни значень коефіцієнтів апроксимації від часу:

. (3.21)

Залежність (3.21) становить часовий ряд зміни параметрів розподілу випадкової величини від часу. Екстраполюючи цей ряд, знаходимо прогнозні значення параметрів розподілу

с(t), t > t_n (3.22)

Тоді прогнозне моделювання величини x – випадкового процесу виникнення державного боргу та випадкового процесу його погашення зведеться до відтворення послідовності чисел, які підлягають прогнозному закону розподілу.

(3.23)

В результаті виконання описаної процедури отримаємо алгоритм імітування послідовності чисел, що є величиною нового виникаючого боргу та величиною зникаючого існуючого боргу.

Описаний метод охоплює відомі способи моделювання випадкових процесів зі змінною дисперсією, іншими параметрами. На його основі, отримавши залежність параметрів апроксимації від часу, легко виконати якісний аналіз модельованої випадкової величини, визначити тенденції її зміни з часом.

За критерієм ідентифікації параметрів моделі описаний метод належить до обчислювальних алгоритмів так званої стохастичної апроксимації, однак він доповнений методами прогнозування параметрів закону розподілу випадкової величини, що дозволяє застосовувати розроблений метод для екстраполяції нестаціонарного стохастичного процесу.

Запропонований метод моделювання фінансових опціонів з пасивами держави дає інструмент для дослідження закономірностей формування державного боргу, дозволяє прогнозувати процеси, що відбуваються на ринку пасивів держави, передбачувати їх монетаризацію, перехід в інші фінансові форми.

Нижче викладено алгоритми вирахування величини боргових зобов’язань з допомогою розробленого методу стохастичної екстраполяції нестаціонарного випадкового процесу.

Алгоритм 3.1 – Прогнозне моделювання фінансового займу держави.

1. Отримати дані (3.14) про щоденну величину державного займу u_k,.k=1,…,m.

2. Вибрати кількість елементів n у ковзній вибірці U (3.17).

3. Вибрати діапазон перекриття двох суміжних ковзних вибірок U_j, U_j+1.

4. Створити масив ковзних вибірок для опціонів державного займу

, (3.24)

5. Встановити дискретно задані закони розподілу (3.19) для масиву ковзних вибірок.

6. Розв’язавши задачу квадратичної нелінійної апроксимації (3.20), встановити значення параметрів алгебричного виразу, вбраного для наближення закону розподілу ковзної вибірки.

7. Повторити розв’язок задачі апроксимації для всіх вибірок (3.24).

8. Встановити значення часу (3.18), зіставленого з ковзною вибіркою.

9. Виконуючи прогнозну екстраполяцію дискретної залежності (3.21) для державного займу, знайти прогнозні значення всіх параметрів, зо входять в алгебричний вираз, вибраний для наближення закону розподілу в ковзних вибірках.

10. Вирахувати прогнозні значення закону розподілу нестаціонарного стохастичного процесу, що описує фінансові опціони державного займу.

11. Згенерувати послідовність чисел, що підлягають знайденому нестаціонарному закону розподілу величини державного займу.

13. Зістававши згенеровану послідовність з дискретними значеннями часу, отримати проноз величини державного займу.

З допомогою алгоритму 3.1 легко вирахувати величину «виникаючого» боргу держави. Для розв’язання другої частини задачі необхідно змоделювати процес погашення державою свого боргу. Алгоритм вирахування цієї величини викладено нижче.

Алгоритм 3.2 – Прогнозне моделювання фінансового займу держави.

1. Отримати дані (3.14) про щоденну величину погашення державного боргу y_k,.k=1,…,m.

2. Вибрати кількість елементів n у ковзній вибірці Y (3.17).

3. Вибрати діапазон перекриття двох суміжних ковзних вибірок Y_j, Y_j+1.

4. Створити масив ковзних вибірок для опціонів державного займу

, (3.25)

5. Встановити дискретно задані закони розподілу (3.19) для масиву ковзних вибірок величини погашення боргу.

6. Розв’язавши задачу квадратичної нелінійної апроксимації (3.20), встановити значення параметрів алгебричного виразу, вбраного для наближення закону розподілу ковзної вибірки величини погашення боргу.

7. Повторити розв’язок задачі апроксимації для всіх вибірок (3.25).

8. Встановити значення часу (3.18), зіставленого з ковзною вибіркою.

9. Виконуючи прогнозну екстраполяцію дискретної залежності (3.21) для величини погашення боргу, знайти прогнозні значення всіх параметрів, зо входять в алгебричний вираз, вибраний для наближення закону розподілу в ковзних вибірках.

10. Вирахувати прогнозні значення закону розподілу нестаціонарного стохастичного процесу, що описує фінансові опціони підчас погашення державою своїх боргових зобов’язань.

11. Згенерувавши послідовність чисел, що підлягають знайденому нестаціонарному закону розподілу, змоделювати величину погашення державою свого боргу.

13. Зістававши згенеровану послідовність величин погашення боргу з дискретними значеннями часу, отримати прогнозне значення цієї величини.

Другий з описаних вище алгоритмів дає послідовність значень, яка імітує нестаціонарний процес погашення державою своїх боргів.

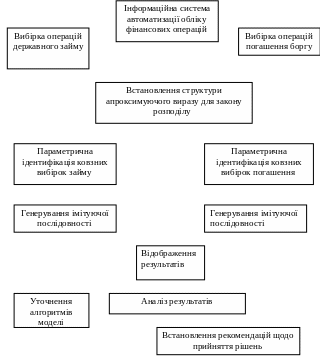
Рис. 2.1. Схема застосування моделі для обчислення величини боргу.

Схематично взаємодію інформаційної системи з даними про обсяги фінансових операцій з пасивами держави, зображено на рисунку нижче.

Під час розробки моделі необхідно виконати ряд робіт, пов’язаних з її проектуванням. Це насамперед пошук даних з минулими значеннями фінансових операцій з пасивами держави. Дальше необхідно встановити інформаційний зв’язок з системою автоматизації, в якій ці дані зберігаються, й програмним забезпеченням моделі. Наступний крок – вибір програмних інструментів для розробки програмного забезпечення моделі.

Після цих підготовчих робіт необхідно реалізувати обчислювальні алгоритми 3.1 та 3.2 і отримати з їх допомогою масиви моделюючих прогнозних значень.

Отримавши прогнозні значення, дальше необхідно провести їх аналіз з точки зору точності моделі та аналіз з точки зору економічного змісту моделюючих даних. На основі цього аналізу виводиться дві групи висновків, які стосуються власне моделі, її алгоритмічної ефективності, достовірності й точності.

Рис. 3.1. Графік виникнення державного боргу

Рис. 3.2. Графік монетаризації державного боргу

Рис. 3.3. Графік погашення державного боргу.

На рисунках 3.1 – 3.3 зображено графіки модельованих величин. На них зображено відповідно щоденні значення сумарних державних боргів, облікованих обласною установою казначейства, щоденну величину монетаризації цих боргів а також величину боргу, погашену протягом окремого дня.

На основі другої групи висновків встановлюються економічні узагальнення щодо особливостей модельованих величин. А також – приймаються рішення відносно досліджуваної задачі – ефективного управління державним боргом.

З допомогою розробленого програмного забезпечення було виконано попередній аналіз даних, що описують державний борг.

Рис. 3.4. Графік лінійної апроксимації виникнення державного боргу.

Рис. 3.5. Графіки лінійної апроксимації монетеризації та погашення державного боргу.

З метою дослідження динамічних властивостей величин, взятих для моделювання, було виконано експерименти з метою встановлення їхніх псевдо-вазових траєкторій у просторі змінних стану, утворених похідними від модельованих величин

Рис. 3.6. Псевдо-фазова траєкторія боргу у просторі [y, y⁽¹⁾, y⁽²⁾].

Рис. 3.7. Псевдо-фазова траєкторія боргу у просторі [y, y⁽²⁾, y⁽³⁾]. Видно, що в досліджуваній системі характерні рухи «перескакують» з одного напрямку простру в інший, що є виявом поведінки типу дивного атрактора.

Рис. 3.8. Псевдо-фазова траєкторія боргу у просторі [y⁽¹⁾, y⁽²⁾, y⁽³⁾].

Попередній аналіз модельованих величин не дає однозначних висновків про доцільність вибору того чи іншого технологічного програмного підходу для розв’язання поставлених задач.

Нижче подано детальніший опис обчислювальних експериментів з модельованими даними та програмним забезпеченням спроектованої моделі.

На рисунках 3.6-3.8 зображено псевдо-фазові траєкторії, вирахувані за величиною боргу. З цих ілюстрацій видно, що динамічна зміна досліджуваної величини належить до рухів, притаманних стохастичним системам і системам з динамічним хаосом. Характерний вихор, утворений у просторі змінних стану, скупчення траєкторій в точці перемішування та розбігання їх на далекі відстані – це звичайні прояви динамічного хаосу, в якому сильно проявляються випадкові рухи.

Рис. 3.9. Типовий вид точкової фазової траєкторії досліджуваної величини.

Тобто, в результаті дослідження псевдо-фазових траєкторій модельованих величин, в них виявлено явища динамічного вихору (рис. 3.6, 3.8), явища перемішування та розбігання траєкторій, явища переходу з одного якісного типу поведінки на інший (рис. 3.7). Ці ознаки вказують, що динаміка виникнення державного боргу, його монетаризації та повного погашення, належать до явищ динамічного хаосу.

Разом з тим, експерименти з вирахування дискретних фазових траєкторій, показаних на рисунку 3.9, показують, що досліджувані величини достатньо близькі до випадкових величин, тобто є реалізаціями стохастичного процесу.

Зауважимо, що єдиним застереженням, яке відрізняє досліджувану величину від стохастичної, є стрімкий перехід зображуючої точки, якій зумовлений різким зростанням державного боргу в 1997 році, який був пов’язаний з масовою позикою держави в комерційних банків. Якщо це явище, а також подібне явище зростання іноземного боргу на початку 2000-х років вважати певним винятком з правила, тоді досліджувана величина є дуже близькою до статистичної вибірки, що відтворює деяких динамічний випадковий процес.

Також для трьох досліджуваних величини – боргу, мнетаризації та повернення боргу було вирахувано коефіцієнти кореляції. Результати цих обчислень показано на рисунку 3.10. Як видно з цих обчислень, всі три величини є сильно скорельовані між собою. Тому застосування одних лише методів моделювання, що ґрунтуються на теорії ймовірності та математичній статистиці, не достатньо для відтворення досліджуваних величин. Адже з точки зору теорії ймовірності кожна з них є репрезентативна по відношенню до решти, тобто інші величини в межах статистичного аналізу можуть бути опущені.

В той же час, відповідно до суті задачі, перша величина – виникнення боргу є причиною двох інших – його монетаризації та погашення, тому замінювати або опускати одну з величин, взятих до уваги немає підстав.

Список вибірок (3 шт.):

0. borg

1. monetaruzac_ia

2. povernenna

Матриця значень t 2-х выборок:

========================================

0 1 2

----------------------------------------

0| 0.0000 101.9025 98.1005

1| 101.9025 0.0000 -3.8020

2| 98.1005 -3.8020 0.0000

========================================

Матриця степеней свободи t-розподілу 2-х вибірок:

======================

0 1 2

----------------------

0| 2080 2080 2080

1| 2080 2080 2080

2| 2080 2080 2080

======================

Матриця коефіцієнтів кореляції 2-х выбірок:

=====================================

0 1 2

-------------------------------------

0| 1.0000 0.9717 0.9892

1| 0.9717 1.0000 0.9663

2| 0.9892 0.9663 1.0000

=====================================

Рис. 3.10 – Коефіцієнти кореляції модельованих величин.

Отже, попередній аналіз особливостей динамічного руху в досліджуваній системі та статистичний аналіз масивів даних, які відображають реальні минулі значення модельованих величин, показують, що для їх прогнозного відтворення не доцільно застосовувати детерміновані методи економіко-математичного моделювання, а також методи, що ґрунтується на імітації статистичних послідовностей.

Тобто, попередній кількісний аналіз досліджуваних даних, підтвердив раніше обґрунтовані припущення, що для моделювання державного боргу доцільно застосувати методи моделювання стохастичних динамічних систем, в яких основні параметри, такі як середньоарифметичне значення, дисперсія тощо, динамічно змінюються з часом.

Для дослідження динамічної зміни з часом випадкових характеристик модельованих величин було застосовано методи багатовимірного кластерного аналізу.

Наявні масиви експериментальних значень, які відповідають дійсним значенням модельованих даних за 1041 робочий день за 1996-2003 роки, було використано для утворення багатовимірної випадкової вибірки. Зокрема – проведено експерименти з двовимірною вибіркою, в якій вузол даних утворений самою величиною та похідною від неї.

Для таких багатовимірних вибірок застосовано методи кластерного аналізу, які полягають у виявленні гіперкуль в просторі даних та у розподілу елементів вибірок між цими гірекулями. Зрозуміло, що з точки зору теорії динамічного хаосу, такий кластер ний аналіз тотожний з виявленням кореляційної розмірності наявних масивів даних.

Рис. 3.11. Ілюстрація розділення 2-вимірної вибірки боргу на 6 кластерів.

Рис. 3.12. Ілюстрація розділення 2-вимірної вибірки монетаризації боргу на 6 кластерів.

Рис. 3.13. Ілюстрація розділення 2-вимірної вибірки повернення боргу на 6 кластерів.

Кластерний аналіз вибірок, отриманих на основі двовимірної величини, утвореної модельованим значенням та похідною від нього, є своєрідними проміжними методом аналізу, який з однієї сторони бере до уваги класичну динаміку процесу, адже аналізована вибірка є дискретною послідовністю точок у псевдо-фазовому просторі, а з іншої сторони – аналізує наявні дані як масиви випадкових величин, котрі з часом змінюють свої статистичні характеристики.

Результати проведеного кластерного аналізу боргу, його монетаризації та погашення, показано відповідно на рисунках 3.11, 3.12, 3.13. Як видно з цих рисунків динаміка боргу, виражена через зміну статистичних параметрів модельованих величин, протягом досліджуваного відрізку часу зазнавала істотних змін. Втім, методами кластернго аналізу виявлено не більше шести історичних областей, протягом яких поведінка держави щодо її боргу якісно відрізнялася.

З цього випливає два висновки. По-перше, є підстави стверджувати, що порядок динамічної системи, яка генерує досліджуваний хаотичний ряд, не є більшим за третій, що прямо випливає х теореми Такенна, якщо кількість кластерів вважати за міру кореляційної розмірності даних.

По друге, послідовна впорядкованість кластерів з часом показує, до для моделювання боргу доцільно відтворити часову зміну статистичних характеристик розподілу нестаціонарної випадкової модельованої величини. Тобто, кластерний аналіз ще раз підтвердив припущення, покладені в основу моделі боргу.

В наступних експериментах було проведено обчислення за алгоритмом 3.1, згідно якого на основі наявного масиву даних з допомогою ковзної вибірки було встановлено закон розподілу модельованої величини для відрізку часу, зо відповідає ковзній вибірці. Потім масив отриманих дискретних законів розподілу апроксимовано і отримано прогнозне значення закону розподілу. На основі цього прогнозного значення закону розподілу, який явно залежить від часу отримано декілька значень прогнозної величини боргу. Ці значення усереднено і отримане середньоарифметичне значення взято за прогнозне значення модельованої величини.

При цьому масив даних було розбито на 22 вибірки розміром 200 елементів, які перекривалися між собою на 50 елементів.

Обчислення повторено для величини боргу, величини його монератризації та величини повернення.

Результати обчислень за названими методом проілюстровані на рисунках нижче.

Рис. 3.14 (а) – Закон розподілу боргу на першій ковзній вибірці.

Рис. 3.14 (б) – Закон розподілу монетаризації на першій ковзній вибірці.

Рис. 3.14 (в) – Закон розподілу погашення боргу на 10 ковзній вибірці.

На основі ряду законів розподілу, встановлених з допомогою ковзних вибірок, встановлено з допомогою поліноміальної апроксимації методом найменших квадратів прогнозне значення розподілу всіх трьох модельованих величин.

Графіки прогнозних значень законів розподілу, вирахуваних га області екстраполяції, подано на рисунку 3.15.

Рис. 3.15 (а) – Прогнозне значення закону розподілу боргу.

Графіки законів розподілу, проілюстровані на рис. 3.15, отримано для одного з моментів часу, що виходить за межі області ідентифікації моделі. Тобто для вузла часової шкали, більшого за 1041.

На основі прогнозної величини закону розподілу, вирахуваної в кожен момент часу на області екстраполяції, вирахувано послідовність випадкових чисел, що підлягають цьому закону розподілу.

Рис. 3.15 (б) – Прогнозне значення закону розподілу монетаризації.

Рис. 3.15 (в) – Прогнозне значення закону розподілу погашення боргу.

Графіки випадкових величин, згенерованих на основі прогнозного значення нестаціонарного закону розподілу показані на рисунках 3.16-3.18.

Рис. 3.16 (а). Реальне та прогнозне значення боргу.

Рис. 3.16 (б). Реальне та прогнозне значення боргу в збільшеному масштабі.

Рис. 3.17 (а). Реальне та прогнозне значення монетаризації.

Рис. 3.17 (б). Реальне та прогнозне значення монетаризації в збільшеному масштабі.

Рис. 3.18 (а). Реальне та прогнозне значення повернення боргу.

Рис. 3.18 (б). Реальне та прогнозне значення повернення боргу в збільшеному масштабі

Рис. 3.19 (а). Прогноз боргу.

Рис. 3.19 (б). Прогноз монератризації боргу.

Рис. 3.19 (в). Прогноз повернення боргу.

Остаточні результати прогнозного вирахування величини боргу та його погашення показано на рис. 3.19. При цьому було обчислено прогноз на 360 днів.

Результати практичного застосування моделі прогнозування фінансових величин, що поєднують властивості випадкових процесів та псевдостохастичних систем, показують, що методи екстраполяції нестаціонарного закону розподілу цих величин з пізнішим відтворенням їх послідовності методами імітаційного моделювання та вирахування прогнозного значення через усереднення отриманих випадкових послідовностей, дають добрі прогнозні результати.

Практично застосований метод поєднує елементи стохастичної апроксимації закону розподілу та моделювання з допомогою методу Монте-Карло, в якому на основі згенерованої статистичної вибірки визначається прогноз як її математичне сподівання.

Аналіз отриманих результатів моделювання показує, що в майбутньому величина державних боргових зобов’язань України зростатиме. Згідно отриманих прогнозів, в майбутньому очікується тенденція зменшення обсягів погашення боргу та зменшення обсягів переведення державного боргу України на ринки торгівлі фінансовими пасивами. Це песимістичний прогноз, який демонструє погіршення фінансового стану України в галузі управління державним боргом.

Отримані прогнозні дані показують, що для покращення фінансової діяльності з борговими зобов’язаннями необхідно вживати комплексних заходів. Що є одним з головних висновків цієї дипломної роботи.

Втім, довготривалий прогноз основних параметрів боргу показує стійкість цієї галузі державних фінансів, що дає добрі підстави для вдосконалення її роботи, взаємного обопільного пожвавлення фінансової діяльності як держави, так й суб’єктів підприємницької діяльності в галузі обігу пасиві. Що також є однією з ознак пожвавлення економки нашої країни.

Висновки. Для розв’язку задачі прогнозного вирахування величини боргу розроблено його математичну модель, записану рівняннями випадкового вінеровського процесу. Виведено ідентифікаційні рівняння цієї моделі, запропоновано алгоритм розв’язку моделюючих рівнянь, які дають прогнозні значення випадкових коливань величини боргу.

На основі запропонованого алгоритму розроблено програмне забезпечення, призначене для імітації величини державного боргу.

З допомогою розробленого програмного забезпечення виконано обчислювальні експерименти з вирахування прогнозної величини державного боргу за різних можливих значень зовнішніх параметрів. Вирахувано величину державного боргу обласного бюджету.

Розкрито ряд закономірностей щодо особливостей формування державного боргу, які приводять до практичних висновків щодо ефективного управління ним.