Практикум з моделювання економіки

Буяк Л.М.

Паучок В.К.

Подано збірку розв’язків різотипних задач, які стосуються математичного моделювання економічних явищ, їхнього дослідження з допомогою обчислювальних експериментів з математичними моделями. Знайдені розвязки моделей супроводжуються економічними інтерпретаціями.

Для студентів та фахівців інженерно-економічних спеціальностей.

© Буяк Л.М. 2006

© Паучок В.К. 2006

©

Передмова

Математичне моделювання економічних явищ лежить на перехресті різних, допевна протеричивих пізнавальних підходів. З однієї сторони – традиції гуманітарної економіки, які воліють відмежовуватися від природничо-математичних методів пізнання, або обмежуватися такими у вузько визначених межах. З іншої сторони – методи природничо-технічних наук, котрі, вільо володіючи математично-інформаційним апаратом, на завжди готові дослуховуватися до суті соціально-економічних явищ, які потрапили в їхнє поле зору.

Крім цього знаного корпоративного протистояння гуманітарних та природничих світоглядів, моделювання економіки обтяжене суб’єктивізмом визначення суті модельованого явища й неоднозначністю його відображення в математичних категоріях.

В пропонованій збірці робіт з моделювання економіки, виконаній укладачами в співавторстві з студентами, авторство яких вказано у кожній праці, зроблено спробу, долаючи тазвані методологічні перепони, показати навчальний підхід, котрий відповідає як інженерному конструктивізму, так і пізнавальному прагматизму. Який показує, як легко з допомогою програмного забезпечення математичних моделей економічних явищ відкриваються нові, часом нетривіальні знання.

Зібрані роботи охоплюють різнопланові підходи як за економічним змістом, математичним апаратом, так і за новизною та повнотою дослідження.

Декі з них, що на переконання авторів, цілоком прийнятно для навчальних цілей, повторюють відомі результати, застосовуючи їх для дещо інших практичних цілей, ніж це було запропоновано авторами. Більшість же робіт відзначається власною новизною. Оригінальноми підходами ро розв’язання задач, новими висновками щодо суті модельованих явищ.

Відповідно до дидактичних підходів авторів – кожна з робіт залишається допевна незавершеною, що адекватно переносить сучасний стан моделювання економіки на виховання нового покоління фахівців цієї галузі.

З уваги на обмежений розмір посібника лише одна робота доповнена текстом програмного забезпечення моделі.

Укладаючи пропонований посібник, автори намагалися зберегти ті досягнення, методологічні, пізнавальні та дидактичні, якими відзначалися Українські школи моделювання в минулі десятиліття.

1. Модель дохідності переробного плодово-овочевого підприємства

Співавтор: Блощинська Олександра Анатоліївна

Побудовано модель дохідності переробного плодоовочевого підприємства у формі виробничої функції, заданої багатовимірним степеневим поліномом від параметрів, що описують стан ангарного й промислового ринків та стан підприємства. Для ідентифікації параметрів моделюючого поліному застосовано метод найменших квадратів, регуляризований з допомогою стабілізуючого функціоналу Тіхонова та з допомогою редукції степеня апроксимуючого поліному. Модель побудовано для стаціонарного випадку, без урахування часу, та для випадку, коли час явно записано переметом багатовимірного поліному.

Поставлено задачу побудувати математичну модель, яка описує взаємозалежність між величиною доходу, який отримує переробне плодоовочеве підприємство, від зовнішніх та внутрішніх чинників, які впливають на величину доходу, і котрі виражають ефективність його діяльності на ринку заготівлі плодів та на ринку збуту продукції. При цьому до уваги береться стан продуктивності підприємства за відносно невеликий проміжок часу, для якого, вважатимемо, параметри, що визначають його, залишаються незмінними.

Розв’язок цієї задачі має дати інформацію про відносне значення окремих факторів, зовнішніх й внутрішніх щодо окремого переробного підприємства, які впливають на величину його доходу, а також сформувати висновки про перспективні шляхи вдосконалення його діяльності, які ведуть до загального підвищення дохідності підприємства.

Встановивши числові значення названих вище параметрів, легко виконувати обчислювальні експерименти, сплановані для виявлення залежності дохідності, від зовнішніх та внутрішніх факторів впливу.

Розв’язання поставленої задачі. Відомо, що дохідність підприємства залежить від зовнішніх та внутрішніх факторів, зокрема, від ефективності діяльності підприємства на ринку закупівлі плодів, та від результативності збутової політики, її маркетингового пристосування до потреб споживачів, запитів рику.

Оскільки немає ніякої апріорної інформації про вплив чинників зі сторони ринку закупівлі плодів, та зі сторони збуту продукції, а також немає даних про вплив, зумовлений внутрішньою організацією виробництва, технічною та фінансовою, тому виберемо структуру моделі, яка зв’язує величину дохідності та інші чинники у формі лінійного алгебричного рівняння. Деколи таке рівняння в задачах моделювання називають рівнянням лінійної регресії або факторним аналізом.

Виберемо для моделювання дохідності економічну результативність роботи одного підприємства.

Нехай d_ik = d_i(t_k) –величина доходу від виготовлення і-тої продукції країни протягом k-го відрізку часу, і=0,...N, k=1,...,m, де N – кількість видів продукції, m – кількість відрізків часу, за які беруться спостережувані дані. Вважатимемо, що величина d_ik відома, причому d_0k позначає сумарний дохід.

Апріорна інформація про вплив окремих факторів на величину доходу доволі обмежена. Тому для побудови алгебричного лінійного рівняння візьмемо дві групи факторів – список основних величин, що описують закупівлю плодів, і список таких же параметрів, що описують внутрішньо-економічний стан окремого підприємства.

Нехай a_ik = a_i(t_k) – величина і-го фактора впливу, де і=1,…,n; k=1,…,m; n – кількість факторів ринку закупівлі товарів аграрного виробництва. Віднесемо до факторів аграрного ринку наступні величини, які подано в таблиці 1.1

Табл. 1.1. Чинники аграрного ринку.

№ пп..	Назва чинника аграрного ринку	Позначення
1	Ціна яблук	a1k
2	Ціна груш	a2k
3	Ціна вишень	a3k
4	Ціна черешень	a4k
5	Ціна полуниць	A5k
6	Ціна порічок	a6k
7	Ціна смородини	a7k
8	Ціна аґрусу	a8k
9	Ціна малини	a9k
10	Ціна ожини	a10k
11	Ціна ревеню	a11k
12	Ціна слив	a12k
13	Ціна абрикос	a13k
14	Ціна помідорів	a14k
15	Ціна баклажанів	a15k
16	Ціна кабачків	a16k

На прибутковість переробного підприємства також впливають фактори, що стосуються ринку промислових товарів – вартість цукру, вартість енергоносіїв, вартість тари того. Позначимо фактори промислового впливу b_ik =b_i(t_k); i=1,…p. Список чинників промислового ринку подано в таблиці 1.2.

Крім названих вище параметрів, зовнішніх щодо підприємства, на його продуктивність впливають внутрішні параметри, що відображають структуру капіталу, технологічний стан виробництва тощо.

На продуктивності позначаються обсяги споживання різних товарів, аграрних і промислових, які купує переробне підприємство для ведення своєї основної виробничої діяльності.

Таблиця 1.2 – Чинники промислового ринку.

№ пп..	Назва чинника промислового ринку	Позначення
	Ціна цукру	b1k
	Ціна дизельного палива	b2k
	Ціна бензину	b3k
	Ціна скляної тари	b4k
	Ціна пакувального матеріалу	b5k

Нехай s_ik =s_i(t_k) – обсяг закупівлі i-го товару на агарних та промислових ринках, де i=1,…,q. Список товарів, які взято до уваги, подано в таблицях 1.1, 1.2.

Опираючись на апріорні дані візьмемо до уваги групу чинників, що відображають фінансовий й технологічний стан підприємства. Це такі величини як продуктивність праці, енергоозброєність одного робочого місця, зарплата одного працюючого тощо.

Нехай x_ik =x_i(t_k)– величини, що відображають фінансовий й технологічний стан підприємства, де i=1,…,K. Список таких величин подано в таблиці 1.3.

Таблиця 1.3 – Внутрішні дохідності підприємства

№ пп.. Назва внутрішнього чинника Позначення

1 Продуктивність праці x_1k

2 Енергоозброєність робочого місця x_2k

3 Матеріалоємність одиниці продукції x_3k

4 Зарплата на одного працюючого x_4k

5 Доходи власника підприємства x_5k

6 Обсяги споживання енергії x_6k

7 Обсяги споживання товарів x_7k

8 Обсяг споживання послуг x_8k

9 Кількість працюючих x_9k

10 Кредиторська заборгованість x_10k

На продуктивність й дохідність підприємства також впливають слабоформалізовані величини, які відображають суспільно-економічний стан.

Нехай _ik – величина слабоформалізованого фактора, який відображає стан суспільства й економіки, в середовищі якої веде господарську діяльність досліджуване підприємство, де i=1,…,M. Список слабоформалізованих параметрів подано в таблиці 1.4.

Введені в розгляд величини (1.1) – (1.5) відомі. Вони опубліковані у відповідних щорічних звітах, також беруться з даних статистичної звітності досліджуваної країни. Значення деяких з цих величини можуть залишатися одними й тими ж самими протягом декількох відрізків часу. Слабоформалізовані значення _ik беруться з публікацій рейтингових показників, які встановлюються різними урядовими й неурядовими організаціями.

Величини x_ik – беруться за k-тий відрізок часу за даними статистичної та аналітичної звітності досліджуваного підприємства.

Таблиця 1.4 – Список слабоформалізованих параметрів.

№ пп..	Назва слабоформалізованого параметра	Позначення
1	Оцінка інвестиційної привабливості	β1k
2	Оцінка сприятливості ведення бізнесу	β2k
3	Оцінка рівня корупції	β3k
4	Оцінка прозорості економічних відносин	β4k
5	Оцінка рівня свободи слова	β5k
6	Оцінка стабільності й передбачуваності	β6k
7	Ефективність законодавства ринкових механізмів	β7k

В результаті прийнятих припущень шукана модель запишеться у формі переозначеної системи лінійних алгебраїчних рівнянь:

(1.1),

Співвідношення (1.1) задає лінійне рівняння, яке зв’язує величину дохідності переробного підприємства d_k протягом m відрізків часу як функцію визначених величин та слабоформалізованих параметрів. Одночасно рівняння (1.1) слугує для ідентифікації параметрів с.

Для встановлення параметрів с моделі (1.1) достатньо розв’язати це рівняння при відомих значеннях a, b, s, x, , застосовувавши, наприклад, метод найменших квадратів.

Рис. 1.1. Структурна схема моделі переробного підприємства, заданої алгебричною виробничою функцією з регуляризованою ідентифікацією параметрів за методом найменших квадратів.

Зазначимо, що для визначення впливу окремих факторів на величину інвестицій необхідно числові масиви даних (табл.. 1.1-1.4) нормалізувати на 1, оскільки ці дані входять в рівняння лінійно, тому така нормалізація не супроводжується зміною рівняння (1.1).

Опишемо поданий вище метод вирахування величини дохідності лінійної функції ряду зовнішніх і внутрішніх, формалізованих і слабоформалізованих чинників у вигляді окремого алгоритму.

Структурно модель, описана вище, зображена на рисунку 1.1.

Обчислення, які необхідно виконати, будуючи модель, описано в алгоритмі нижче.

Алгоритм 1.1. Вирахування величини інвестицій як функції параметрів інвестиційної привабливості.

1. Встановити сумарну величину доходу від продажі всіх видів товарів d_0k і величину доходу d_ik від продажі і-того товару протягом k-го року i=1,…,n; j=1,…,m.

2. Встановити величину чинників a_ik аграрного ринку згідно таблиці 1.1 протягом k-го відрізку часу, де i – номер фактора впливу: i=1,…,n; k=1,…,m.

3. Встановити величину чинників b_ik промислового ринку згідно таблиці 1.2 протягом k-го відрізку часу, де i – номер фактора впливу: i=1,…,p; k=1,…,m.

4. Встановити обсяг закупівлі продуктів аграрному ринку і товарів на промисловому ринку s_ik згідно таблиць 1.1 та 1.2 протягом k-го відрізку часу, де i – номер фактора впливу: i=1,…,q; k=1,…,m.

5. Встановити величину показників фінансового та економічного стану підприємства x_ik згідно таблиці 1.3 протягом k-го відрізку часу, де i – номер показника, i=1,…,K; k=1,…,m.

6. Встановити величину слабоформалізованих факторів _ik впливу на величину дохідності від продаж і-того товару протягом k-го року, де i – номер фактора: i=1,…,M; k=1,…,m.

7. Розв’язати рівняння (1.1) відносно невідомих коефіцієнтів апроксимації с.

Обчислювальні експерименти виконані з моделлю (1.1) дають дві групи результатів.

За відносними значенням коефіцієнтів апроксимації с та їх знаком, які отримані з (1.1) при нормалізації на одиницю вектор-стовпців матриці в правій частині (1.1) виводяться висновки про міру впливу відповідного чинника на дохідність підприємства.

Також модель (1.1) при абсолютних значеннях коефіцієнтів c (без нормалізації матриці відомих коефіцієнтів) дозволяє ставити експерименти з вирахування залежності величини дохідності від величини одного чи декількох факторів впливу – аргументів a, b, s, x, β у правій частині рівняння (1.1).

Обидва типи експериментів приводять до якісних висновків щодо управління виробничою діяльністю підприємства, показують, яких планових та бажаних значень показників рекомендовано досягнути, щоб покращити дохідність підприємства. Це дає важливі практичні висновки, адже стосується основ господарської діяльності. Загальність цих висновків пов’язана з найширшим урахуванням всіх чинників, внутрішніх та зовнішніх, які діють на підприємство. Зауважимо, що ці висновки отримані для лінійної моделі, і статичного випадку, в якому часова зміна параметрів не враховується. Тобто вони стосуються невеликих відрізків часу в майбутньому.

Також застосування моделі (1.1) з ідентифікованими параметрами c обмежене малою зміною аргументів a, b, s, x, β. Практично, вибираючи модельне значення аргументів, необхідно обмежуватися областю, близькою до області їх значень, на яких ці аргументи були ідентифіковані. Тобто, модельні значення аргументів мають належати області ідентифікації або виходити за неї не більше ніж на величину, спів мірну з шириною області ідентифікації. При більших відхиленнях аргументів модель втрачає зміст.

В результаті обчислень, виконаних за алгоритмом 1.1, отримано найзагальніші висновки про вплив тих чи інших чинників, параметрів ринку та показників діяльності підприємства, на стан його дохідності, повної, та в розрізі окремих товарів.

Дальше описано інший підхід до моделювання цих же даних (табл.. 1.1-1.4) – модель причинно-наслідкового зв’язку між величиною інвестицій та їх результативністю в якому величина доходу та впливаючі параметри зв’язані нелінійним алгебраїчним співвідношенням, яке відображає статичні особливості цього зв’язку, усереднені за останні роки.

Дохідність підприємства є економічним наслідком ряду причин, зовнішніх ринкових впливів, внутрішніх показників стану підприємства. Тому є підстави вважати, що дохідність протягом невеликих проміжків часу описується деякою невідомою функцією багатьох аргументів

Р ис. 1.2. Схема залежності доходів від параметрів впливу. Невідома виробнича функція зв’язує дохідність з параметрами ринку як величини, що перебувають у причинно-наслідковій залежності. Дохідність є «реакцією» виробничого підприємства на «зовнішні впливи» ринку.

Схематично зв’язок між зовнішніми впливами u(t) та їх результатом y(t) зображено на рисунку 1.2.

В загальному випадку схему, зображену на рис. 1.2 описує система диференційних або інтегральних рівнянь. Проте, якщо до розгляду беруться дані за відносно невеликий проміжок часу, тоді, опускаючи динамічний зв’язок між u₁(t),….,u_n(t) та y(t), правомірно припустити, що ці величини зв’язані деяким алгебричним співвідношенням:

y=F(u₁,…,u_n;c) (1.2)

яке дійсне для відносно невеликого проміжку часу [t₀, t_k]. В нашому випадку – це проміжок часу, співмірний відрізком часу, для якого взято дані для ідентифікації.

В рівнянні (1.2) величину дохідності позначено y, величину зовнішніх впливів позначено u_i, i=1,…,n що відповідає позначенням, які прийняті при моделювання систем виду «чорної скриньки». Зовнішні впливи u_i, i=1,…,n визначені з задачі (1.1) як істотні параметри, що впливають на дохідність. Неістотні параметри з табл. 1.1-1.4, які слабо впливають на дохідність (1.1) в структурі (1.2) опущено.

В загальному випадку функція F(...) – невідома. Записавши співвідношення (1.2) для m експериментальних даних, отримаємо пере-означене рівняння х невідомими коефіцієнтами апроксимації с:

y_k=F(u_1k,…,u_nk;c); k=1,…,m. (1.3)

Припустимо, що рівняння (1.2) має розв’язок відносно величини параметрів с. Зокрема, для пошуку цих параметрів, придатні методи лінійного програмування, метод найменших квадратів, лінійний або нелінійний відносно невідомих коефіцієнтів.

(1.4)

Тому модель (1.2) з ідентифікаційними рівняннями (1.4) придатні для побудови статичної моделі взаємозв’язку між факторами впливу на продуктивність переробного підприємства і дохідністю його виробничої діяльності.

Обґрунтований вибір структури алгебричного виразу F(…) становить одну з проблем моделювання. Проте, в поставленій задачі пошук структури виразу F() спрощується. В рівнянні (1.1) за структуру моделі було взято лінійну комбінацію параметрів, що впливають на роботу підприємства. Вищої точності моделі при звуженні області прийнятних значень її аргументів легко досягнути, взявши за невідому функцію F() квадратичний поліном.

. (1.5)

де i=1,…,m, j=1,2 – невідомі коефіцієнти апроксимації.

Рівняння (1.5) дає вищу точність в порівнянні з рівнянням (1.2), (1.4). Якщо 2n≤m тоді система (1.5) має розв’язок відносно коефіцієнтів с. Припустимо, що розв’язок (1.6) відносно c знайдено. Тоді рівняння (1.5) відображає причинно-наслідковий взаємозв’язок між факторами впливу на продуктивність підприємства та його дохідністю. Модель (1.5) з ідентифікаційними рівняннями (1.4) придатна для проведення статичних експериментів з метою пошуку шляхів покращення дохідності підприємства.

Опишемо викладений вище метод у стислому алгоритмі.

Алгоритм 1.2 – Квадратична алгебрична модель дохідності.

1. Отримати значення y_k величини сумарного доходу переробного підприємства за k-тий відрізок часу.

2. Отримати значення u_ik – параметрів впливу на діяльність підприємства за k-тий відрізок часу.

3. З розв’язку рівняння (1.4), (1.5) знайти коефіцієнти апроксимації i=1,…,m, j=1,2.

4. Вирахувати за формулою (1.5) величину впливу параметрів u_i на дохідність підприємства.

5. Виконати якісний аналіз отриманої алгебричної моделі.

Описаний алгоритм дозволяє виконувати обчислювальні експерименти з метою розкриття кількісних залежностей дохідності від значення основних параметрів, що впливають на нього. Зокрема, модель (1.5) дозволяє шукати частинні похідні від дохідності за параметрами, тобто визначати величину, яку в класичному економічному аналізі називають леверіджем. Леверідж вказує чутливість модельованої величини щодо параметрів, від яких вона залежить.

Зауважимо, щоб досягнути порівняння левіріджу між собою для різних аргументів функції багатьох змінних (1.5) при відомих коефіцієнтах апроксимації, в матриці задачі методу найменших квадратів необхідно спершу нормалізувати елементи вектор-стовпців на одиницю, враховуючи, що аргументи в різних стовпчиках записані у різних степенях.

Експерименти з моделлю (1.1) мають визначити, які параметри найбільше впливають на дохідність переробного підприємства. На цій основі необхідно, вибравши декілька – порядку десяти величин, що чинять найбільш істотний вплив, побудувати модель (1.4), (1.5). Якісний аналіз цієї моделі має дати висновки про найчутливіші параметри, тобто вказати напрямки стратегічного вдосконалення управління підприємством.

Вище було обґрунтовано метод визначення найбільш впливових показників, що позначаються на дохідності переробного плодоовочевого підприємства. Зокрема, показано, як з допомогою лінійної статичної моделі звузити коло чинників впливу і описано метод побудови квадратичної поліноміальної моделі, яка дозволяє впорядкувати ці виділені параметри за чутливістю модельованої системи щодо них.

Проте описані два методи залишаються достатньо неточними. Так, лінійний метод, хоч зберігає кращі екстраполяційні властивості, є менш точним навіть на області ідентифікації. Квадратична модель має невелику область екстраполяції, тобто допускає лише незначні маніпуляції з пошуком шляхів вдосконалення роботи підприємства.

Тому поставлено задачу розробити поліноміальну квадратичну модель дохідності підприємства на основі врахування найбільш впливових чинників, що позначаються на дохідності підприємства.

Загальна формула алгебраїчної залежності, що зв’язує дохідність y з факторами впливу (u₁,…,u_n) згідно теореми Стоуна-Веєрштрасса апроксимується степеневим багатовимірним поліномом:

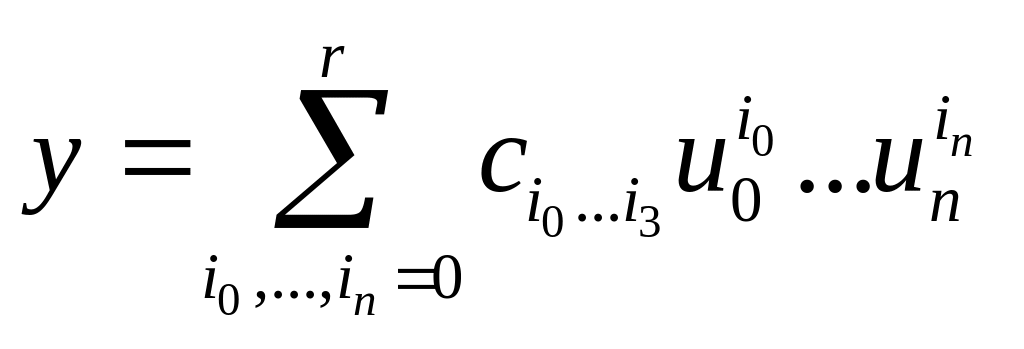(1.6)

де (i₀,…,i_n) – мультиіндекс, причому

(1.7)

де r – степінь багатовимірного полінома (1.5).

Коефіцієнти апроксимації cі багатовимірного степеневого полінома знаходяться з умови мінімізації методом найменших квадратів. Проте суттєва некоректність цієї задачі потребує застосування методів регуляризації. Тому для пошуку коефіцієнтів апроксимації було застосовано мінімізацію регуляризаційного функціоналу Тіхонова:

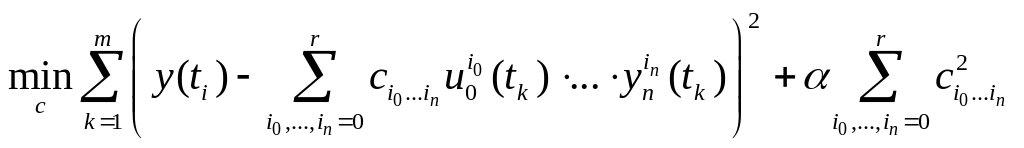(1.8)

Оскільки багатовимірний степеневий поліном (1.5) містять велику кількість доданків, задача (1.6) є суттєво некоректною в сенсі Адамара і тому, для її розв’язання необхідно застосовувати алгоритми регуляризації.

В [¹] для розв’язку рівняння (1.8) запропоновано метод, який полягає у поєднанні регуляризації з допомогою стабілізуючого функціоналу Тихонова. Однак вектор с з задачі (1.8) далеко не завжди дає бажану якість (1.6), адже в поліномі в правій частині цього рівняння записано велику кількість доданків, багато з яких мають низьку інформаційну цінність. З уваги на це в[²] запропоновано метод додаткової регуляризації задачі (1.8), який полягає у виявленні та видаленні “зайвих” доданків апроксимаційного степеневого поліному (1.6).

Для цього у множину значень y_k та (u_1k,…,u_nk) з вносяться невеликі випадкові збурення, двічі розв’язується задача (1.8) без збурень і зі збуреннями та видаляється той доданок полінома, коефіцієнт якого отримав внаслідок збурень найбільше відносне відхилення:

(1.9)

де ĉ_i, c_i – i-ті коефіцієнти апроксимації збуреної та незбуреної задач (1.8).

В результаті редукції степеня апроксимаційного поліному (1.6) отримуємо вираз, який достатньо точно відтворює апроксимовану залежність і не містить “зайвих” доданків, що суттєво покращує якість апроксимації (1.6), а, отже, й точність побудованої поліноміальної регресійної моделі.

Нижче подано стислий виклад алгоритму побудови регуляризованої алгебричної моделі дохідності підприємства від основних величин, що впливають на неї.

Алгоритм 1.4. Регуляризована поліноміальна модель дохідності.

1. Отримати значення доходу y(t_k), k=1,…,m переробного підприємства.

2. Визначити список декількох параметрів (u₁(t_k),…, u_n(t_k)), k=1,…,m, що найсуттєвіше позначаються на його діяльності і отримати значення цих величин.

3. Вибрати початкову степінь r апроксимаційного полінома (1.6).

4. Виконати редукцію степеня полінома за алгоритмом, описаним вище.

5. Знайти коефіцієнти апроксимації сі для редукованого апроксимаційного базису.

Описаний алгоритм дозволяє знаходити точні нелінійні алгебраїчні моделі, що описують зв’язок величини інвестицій та інших економічних факторів з параметрами, які відображають ефективність інвестицій. Завдяки вищій точності, в порівнянні з регресій ними лінійними моделями та регресій ними моделями у формі так званих гравітаційних рівнянь запропонована поліноміальна багатовимірна модель дає інструмент для дослідження впливу величини інвестицій на показники інвестиційної активності при відносно невеликих змінах експериментальних значень інвестицій. З допомогою розробленої моделі легко ставити обчислювальні експерименти, сплановані для виявлення ефективності інвестицій та розкриття впливу інших чинників внутрішніх і зовнішніх, на ефективність інвестування.

Отже, розроблено низку з трьох алгебричних моделей, які в комплексі дозволяють розв’язати задачу оцінки дохідності переробного підприємства. Лінійна модель дозволяє експериментально встановити групу параметрів котрі суттєвіше позначаються на обсягах інвестицій в економіку однієї країни. Квадратична модель, зв’язує результативність підприємства з параметрами, що мають найістотніший вплив.

На основі експериментальних даних щодо найістотніших факторів впливу на дохідність розроблено регуляризовану модель, задану багатовимірним степеневим поліномом, який зв’язує дохідність з показниками впливу на неї.

Для ідентифікації багатовимірної поліноміальної моделі застосовано алгоритм регуляризації з використанням методів стабілізуючого функціоналу Тихонова та функції апроксимаційного базису.

Запропонований підхід дозволяє виявити групу величин, від яких найсуттєвіше впливають на дохідність, впорядкувати ці величини за чутливістю дохідності до їх малих змін, і отримати точну нелінійну поліноміальну модель дохідності.

Отримана в такій спосіб модель дає достатньо точний математичний опис реальної економічної дохідності. Експерименти з нею відкривають нові знання щодо економічних тенденцій, що мають місце в економічних стосунках. Виявлення цих тенденцій, оцінка їх числових значень дає підстави для обґрунтованих рішень при плануванні роботи переробного підприємства, що своєю чергою вдосконалює не тільки його роботу, а й стан аграрного ринку та ринку збуту плодоовочевої продукції.

Також розроблена модель, що є багатовимірною виробничою функцією з регуляризованим алгоритмом ідентифікації, придатна для використання як елемент в інших моделях, зокрема – динамічних моделях взаємодії одного підприємства з оточуючим ринковим середовищем.

На основі описаних алгоритмів розроблено програмне забезпечення і з його допомогою проведено ряд експериментів, послідовно спланованих для дослідження даних, до описують підприємство, дослідження самого підприємства на основі цих даних та побудови його моделі у формі стаціонарної та нестаціонарних виробничих функцій, заданих алгебричними співвідношеннями, описаними в розділі 2.

Для побудова моделі дохідності було вибрано декілька величин, взятих з інформаційних систем матеріального обліку на складах виробничих цехах підприємства.

Зокрема для опису підприємства взято середні значення ціни ягід, плодів, цукру, тари, ціни виготовленого продукту та дохід. Ціни названих матеріалів вирахувано як середні за залишком на складі на кінець дня. Це середнє значення вирахувано як частку кількості коштів, внесених за товар, поділену на величину залишку товару. Ціну готової продукції вирахувано як середнє значення вартості продукції всього асортименту, поділену на кількість одиниць продукції.

Також всі названі вище ціни та щоденні значення доходів перетворено з допомогою лінійного перетворення з метою захисту комерційних інтересів досліджуваного підприємства.

Для моделювання було взято дані за півтора року, що відповідають 2004-2005 рокам.

Графіки модельованих величини зображено на ілюстраціях 1.1 – 1.6.

Перед застосуванням наявних даних для ідентифікації параметрів моделі, ці дані було згладжено з допомогою функції виділення тренду. Як з’ясувалося експериментально, згладження тренду полегшує розв’язок задачі параметричної ідентифікації.

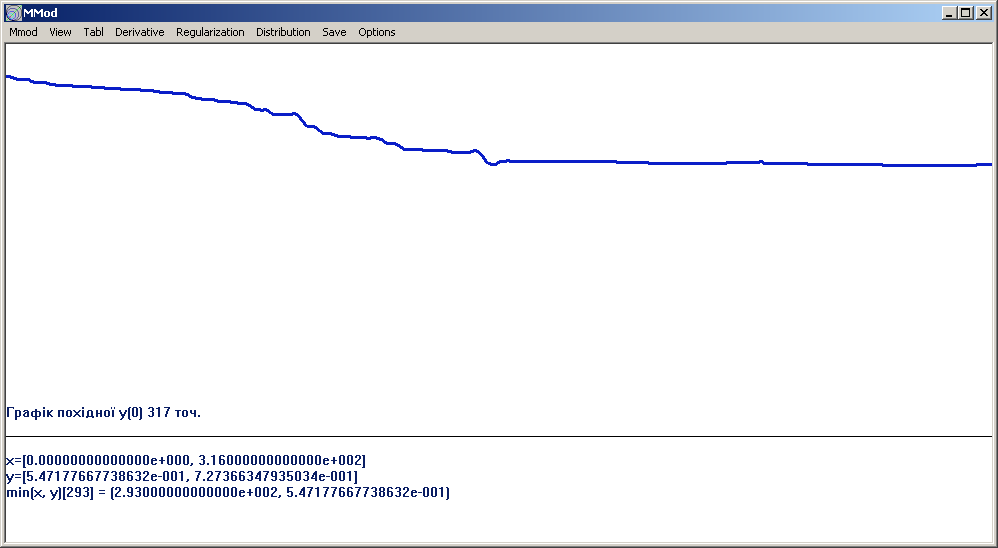
Рис. 1.1. Графік ціни ягід за 2004-2005 рр. Ціну ягід визначено за середнім значенням, яке вирахуване як відношення облікової вартості запасу ягід, куплених за різними чинами, до маси цього запасу. Спад ціни ягід зумовлений зміною структуру запасу, що викликано неврожаями та шкодою, завданою садівництво через посухи та сильні морози.

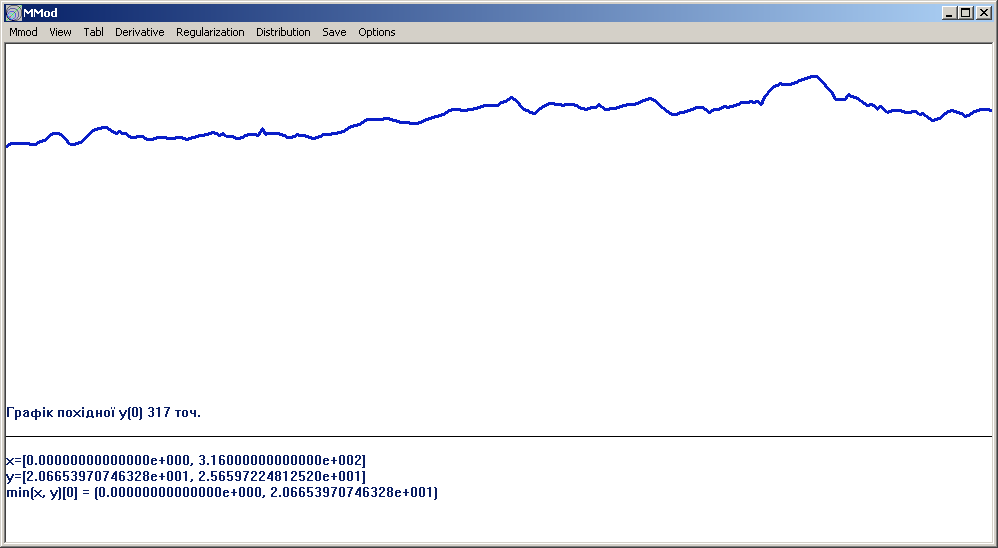
Рис. 1.2. Графік щоденних значень ціни плодів за 2004-2005 рр.. Ціну визначено за середньою обліковою вартістю запасу.

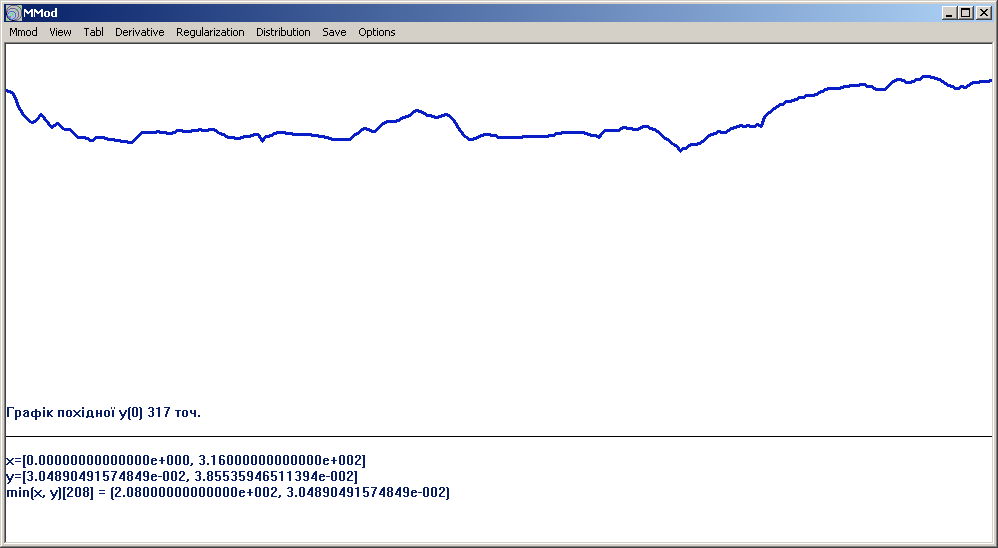
Рис. 1.3. Графік щоденних доходів плодоовочевого підприємства за 2004-2005 рр.

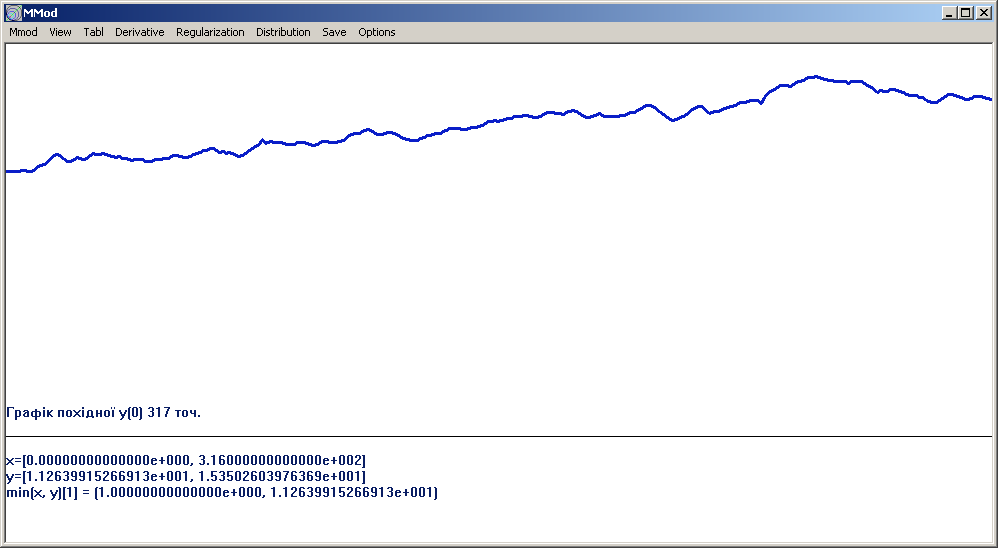
Рис. 1.4. Графік щоденних значень середньої облікової вартості тари за 2004-2005 рр.

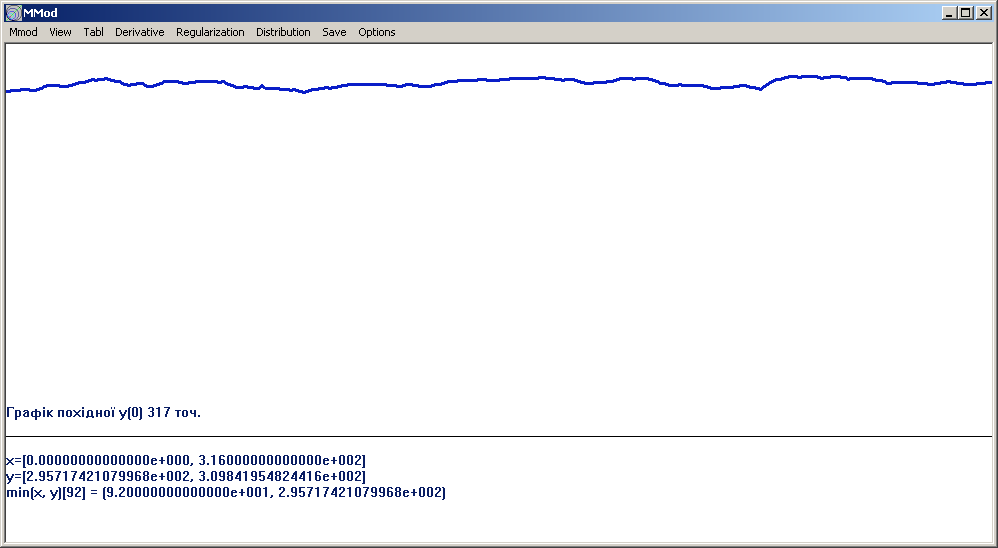
Рис. 1.5. Графік щоденних значень середньої ціни готової продукції за 2004-2005 рр.

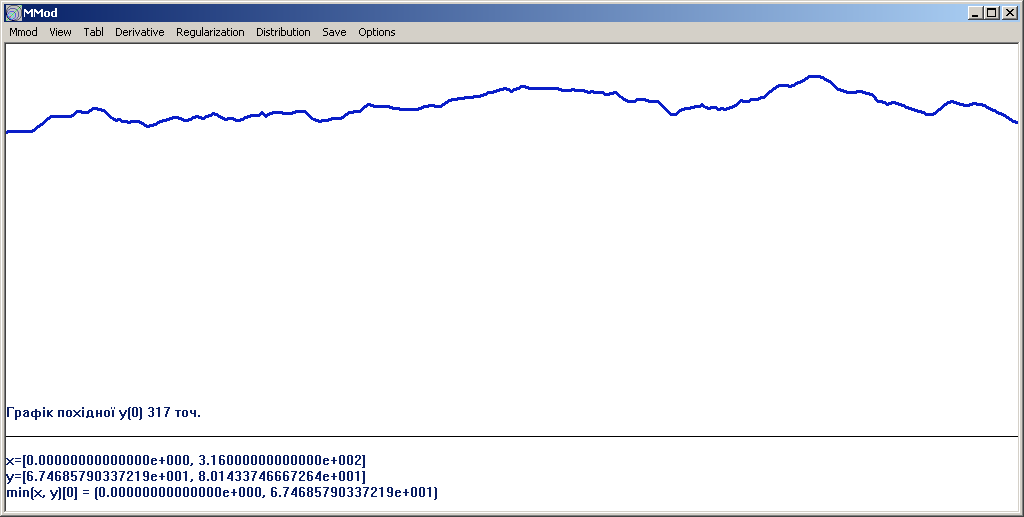
Рис. 1.6. Графік щоденних середніх облікових значень ціни цукру.

Спершу для вибраних даних (рис. 3.1 – 3.6) було вирахувано основні статистичні показники. Результати цих обчислень подано на рисунку нижче.

Список вибірок (6 шт.):

0. ціна ягід

1. ціна плодів

2. ціна цукру

3. ціна тари

4. ціна продкту

5. дохід

Матриця значень t 2-х вибірок:

===========================================================================

0 1 2 3 4 5

---------------------------------------------------------------------------

0| 0.0000 -180.0024 4.5965 -103.4044 -2466.0692 -103.4044

1| -180.0024 0.0000 184.5989 76.5980 -2286.0669 76.5980

2| 4.5965 184.5989 0.0000 -108.0009 -2470.6658 -108.0009

3| -103.4044 76.5980 -108.0009 0.0000 -2362.6649 -0.0001

4| -2466.0692 -2286.0669 -2470.6658 -2362.6649 0.0000 2362.6648

5| -103.4044 76.5980 -108.0009 -0.0001 2362.6648 0.0000

===========================================================================

Матрица степенів свободи t-розподлів 2-х вибірок:

========================================

0 1 2 3 4 5

----------------------------------------

0| 632 632 632 632 632 632

1| 632 632 632 632 632 632

2| 632 632 632 632 632 632

3| 632 632 632 632 632 632

4| 632 632 632 632 632 632

5| 632 632 632 632 632 632

========================================

Матриця коефіцієнтів кореляції 2-х вибірок:

======================================================================

0 1 2 3 4 5

----------------------------------------------------------------------

0| 1.0000 -0.8470 -0.3898 -0.8982 -0.4155 -0.8982

1| -0.8470 1.0000 0.3351 0.9015 0.6414 0.9015

2| -0.3898 0.3351 1.0000 0.5809 0.2256 0.5809

3| -0.8982 0.9015 0.5809 1.0000 0.5295 1.0000

4| -0.4155 0.6414 0.2256 0.5295 1.0000 0.5295

5| -0.8982 0.9015 0.5809 1.0000 0.5295 1.0000

======================================================================

Рис. 1.7. Результати обчислення статистичних параметрів величин, взятих для побудови моделі дохідності переробного підприємства.

Як видно з порівняння t-параметрів та коефіцієнтів кореляції між вибраними величинами немає статистичного зв’язку. Тому для побудови моделі підприємства, зокрема – імітації його роботи немає підстав застосовувати методи теорії ймовірності. Це експериментально підтверджує правильність вибору концептуальної моделі, описаної вище.

Для подальших обчислень масиви даних, зображені на графіках на рис. 3.1 – 3.6, було нормовано на одиницю. Це полегшує обчислення і не зменшує загальності задачі, адже для дослідження було взято дані, піддані лінійному перетворенню.

На рисунку 3.8 зображено графіки величин, які впливають на кінцеву продуктивність, та графік доходів підприємства. На роботу підприємства впливають «причини» – ціна ягід, плодів, тари, цукру, готової продукції. Це аргументи невідомої шуканої виробничої функції. Результатом роботи підприємства є дохід. Це значення невідомої шуканої виробничої функції. Тобто модель підприємства – це «чорна скринька», задана невідомою виробничою функцією, з вхідними величинами ціною ягід, плодів, тари, цукру, готової продукції. Та вихідною величиною – доходом.

На рисунку 1.8 зображено графіки вхідних та вихідної величин моделі підприємства, побудовані за реальними даними. Ці реальні дані застосовано для ідентифікації параметрів моделі.

В першому експерименті для виділених вхідних та вихідної величини було вирахувано їхню лінійну екстраполяцію. Графіки лінійного прогнозу цін та доходів показано на рисунку 1.9. Графіки порівняння реальних значень та їх лінійних екстраполяцій показано на рисунку 1.10.

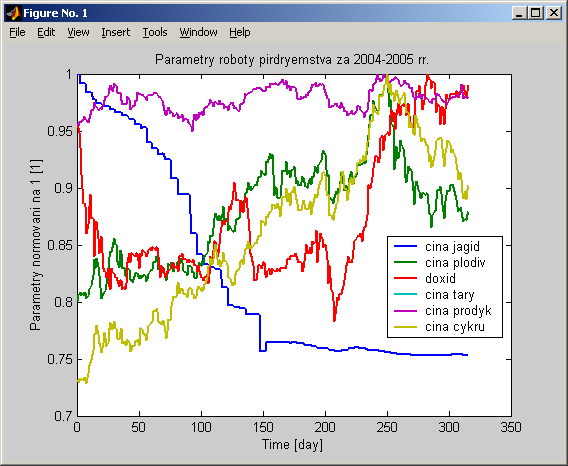
Рис. 1.8. Графіки реальних значень вхідних та вихідної величин моделі підприємства. Ці ж дані, що на рисунках 1.1 – 1.6.

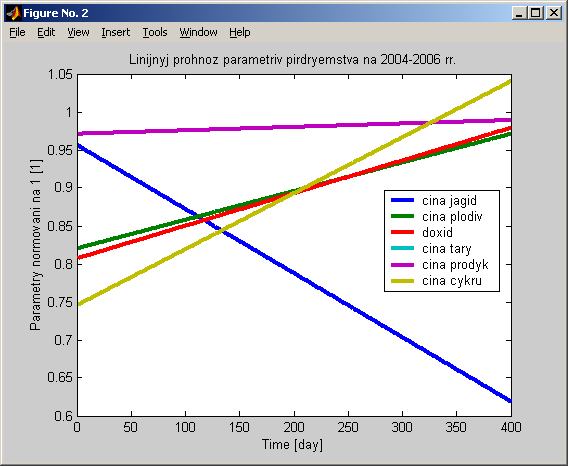
Рис. 1.9. Графіки лінійних екстраполяцій вхідних та вихідної величин моделі підприємства.

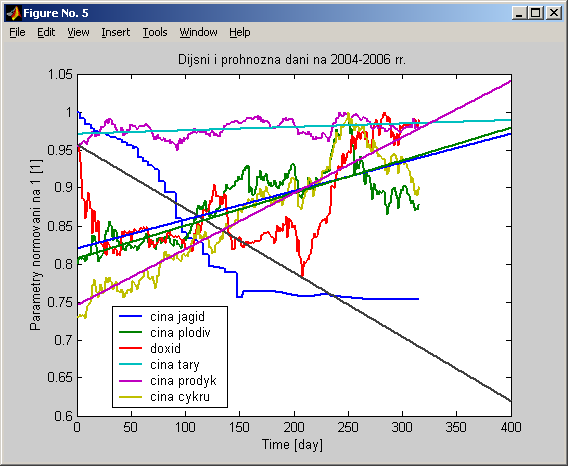
Рис. 1.10. Графіки реальних і прогнозних значень вхідних та вихідної величин моделі.

Як видно з рисунку 1.10, лінійна екстраполяція доволі точно відображає основні тенденції, крім ціни ягід. Остання величина зазнає спаду і стабілізується на значно нижчому рівні. Як зазначалося в огляді стану галузі, це пов’язано з сильним руйнуванням ягідництва в Україні, внаслідок чого змінилася структура заготівлі ягід, в якій почали переважати дешевші вишні й черешні, що призвело до зниження середньої ціни на ягоди, які заготовляє підприємство.

В другому експерименті було вирахувано параметри лінійної алгебричної моделі, яка зв’язує нормалізовані значення доходу з нормалізованими значеннями ціни ягід, плодів, цукру, тари і готової продукції. Значення знайдених коефіцієнтів моделі подано в рівнянні лінійної моделі на рисунку нижче 3.11. Графічно значення коефіцієнтів лілійної регресії показано га рисунку 3.12.

Рис. 1.11. Рівняння лінійної регресії, що зв’язує дохід підприємства, з факторами впливу – ціною ягід, ціною тари, ціною продукту. Видно, що дохід не залежить від ціни цукру. Відповідний коефіцієнт рівний нулю.

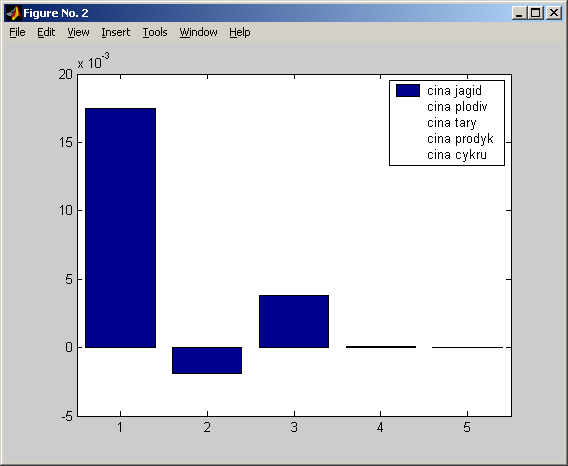
Рис. 1.12. Діаграма значень коефіцієнтів лінійної залежності нормованої величини доходів (4) від нормованих величини ціни ягід (1), ціни плодів (2), ціни тари (3), ціни цукру (5).

Як видно з рисунків 1.11, 1.12 дохід підприємства не залежить від ціни цукру. Цей, на перший погляд парадоксальний висновок, пов’язаний з тим, що підприємство повністю і доволі точно «перекладає» ціну цукру на ціну готової продукції, враховуючи навіть витрати на складське зберігання запасу цукру. Це свідчить про високий рівень організації фінансового планування на підприємстві, але, на жаль, не є показником високої продуктивності його роботи.

Другий висновок, що випливає з аналізу отриманого рівняння лінійної регресії, полягає в тому, що на дохід підприємства мало впливає ціна готової продукції. Це очевидний наслідок того, що на ринку встановилася оптимальна ціна на плодоовочеву продукцію як на товар, що не належить до продуктів першої необхідності. Це невтішний висновок. Адже він показує, що основний харчовий продукт, традиційний для українців, став недоступний, його споживають як предмет дорогий товар, що виходить за споживчий кошик предметів першої необхідності. Для підприємства це означає, що до збільшення доході від виробництва плодоовочевої продукції веде покращення якості продукції, урізноманітнення її асортименту, виробництво подібних товарів різної вартості – «цінових ліній» для плодоовочевих товарів.

На дохідність підприємства значний вплив мають ціни ягід, овочів і тари. Причому від’ємне значення коефіцієнта регресії для тари показує, що підприємство зазнає збитків, вживаючи дорогу тару. Тобто, тару необхідно купувати дешеву, а не «перекладати» на покупців вартість дорогої тари.

Найбільше в лінійній моделі регресії дохід залежить від ціни ягід. Очевидно, це пов’язано не стільки з важливість ягідної продукції, скільки з суттєвими структурними змінами в постачанні ягід, що викликано як природними умовами минулих років, так й триваючим економічним руйнуванням садівництва та особливо ягідництва.

Отже для розв’язання поставленої задачі – побудови нелінійної багатовимірної виробничої функції було вибрано три аргументи – ціну ягід, овочів і тари.

Ідентифікаційне рівняння задачі багатовимірної поліноміальної апроксимації виробничої функції розв’язано з допомогою методу найменших квадратів з застосуванням регуляризаційного функціоналу Тіхонова та редукції степені апроксимаційного полінома. Знайдений розв’язок показано у формі багатовимірного степеневого полінома на рис. 1.13.

Рис. 1.13. Рівняння багатовимірної виробничої функції, заданої степеневим поліномом. Коефіцієнти полінома знайдені з допомогою методу найменших квадратів, регуляризованого з допомогою функціоналу Тіхонова та редукції апроксимаційного базису.

Знайдена багатовимірна виробнича функція відображає поведінку підприємства за реальних умов, що відповідають його діяльності протягом 2004-2005 років. На рисунку 1.13 позначено y₁ – ціна ягід, y₂ – ціна овочів, y₃ – ціна тари.

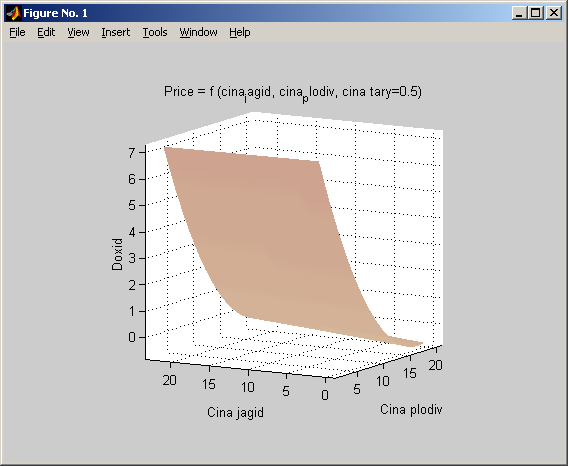
Рис. 1.14 (а). Проекція розв’язку моделі (площини, заданої рівнянням, записаним на рис. 1.13) на простір ціна ягід –ціна овочів – дохід (перший вид).

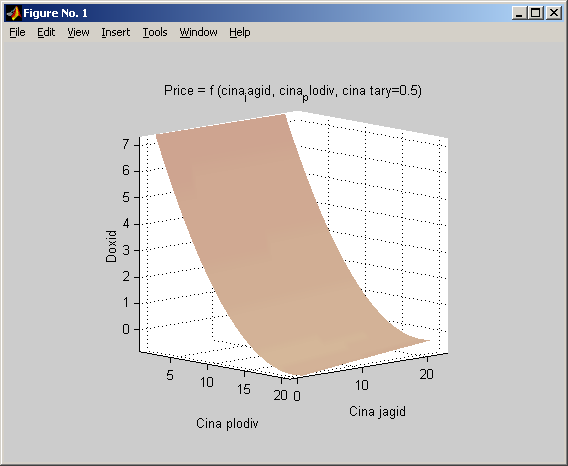
Рис. 1.14 (б). Проекція розв’язку моделі на простір ціна ягід –ціна овочів – дохід (другий вид).

Рис. 1.14 (в). Проекція розв’язку моделі на простір ціна ягід –ціна овочів – дохід (третій вид).

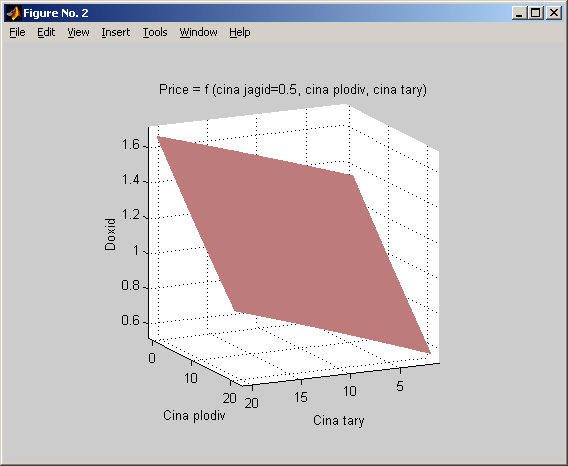
Рис. 1.15. Проекція розв’язку моделі на простір ціна тари –ціна овочів – дохід.

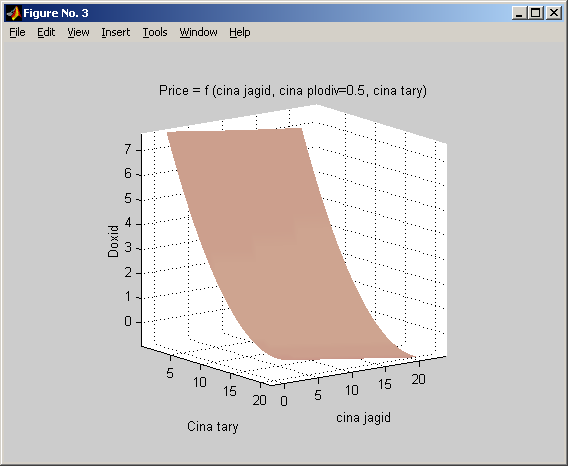
Рис. 3.16. Проекція розв’язку моделі на простір ціна тари –ціна ягід – дохід.

Як видно з графіків на рисунках 1.14 – 1.16 Дохід підприємства суттєво залежить від зростання ціни ягід, мало залежить від зростання ціни овочів і мало обернено-пропорційно залежить від ціни тари. Причому дохідність залежить від ціни ягід та ціни тари як квадратична вгнута крива. Тобто, прискорено зростає зі збільшенням цих величин. Ціна овочів та ціна тари виступають як альтернативні параметри, причому їх вплив у широкому діапазоні значень залишається лінійний.

З цього випливає основний висновок щодо покращення роботи досліджуваного підприємства. Його стан у вирішальній мірі залежить від стану сільського господарства, особливо садівництва, вирощування поживних та рідкісних садових культур. Вплив промислового виробництва на діяльність плодоовочевого підприємства, зокрема – цукрової промисловості нівелюється через тактичне планування закупівлі овочів масового вирощування, пошуком дешевої тари, калькуляцією ціни відповідно до вартості цукру, тари та інших інгредієнтів.

Своєю чергою розвиток садівництва, відновлення популярності цієї галузі потребує тривалого часу та значних капіталовкладень, пов’язаних з довгою тривалістю виробничого циклу. Тому становлення плодоовочевої галузі не може бути швидким.

З аналізу побудованої статичної моделі випливає, що плодоовочеве підприємство найбільш чутливе до зміни асортименту ягідної продукції, причому від покращення її різноманітності та кількості прибутки збільшуються найшвидше. Аналогічний вплив різноманітності овочевої продукції призводить до меншого зростання доходів. Закупівля ж дорожчої, якіснішої тари має негативний економічний результат, який, втім, може бути частково компенсований через пошук дешевших продуктів на аграрному ринку.

Останнє зауваження показує, що переробне плодоовочеве підприємство виконує своєрідну проміжну макроекономічну функцію щодо зважування інтересів аграрного та промислового виробників. Зокрема, в його роботі виникають тенденції заниження доходів аграрного виробника відносно доходів промислового виробника, зайнятого постійним технічним переоснащенням виробництва. Це вказує та те, що переробні плодоовочеві підприємства потребують державних дотацій, які би спрямовували потік капіталу в аграрний сектор. Інакше – спостерігається відтік з аграрного сектору в пакувальну галузь промисловості.

В наступному експерименті, за вихідними даними, проілюстрованими на рисунках 1.1-1.6, побудовано нестаціонарну алгебричну модель, у якій одним з аргументів виробничої функції – багатовимірного степеневого поліному виступає час. Результати побудови цієї моделі проілюстровані на рисунках 1.17-1.19.

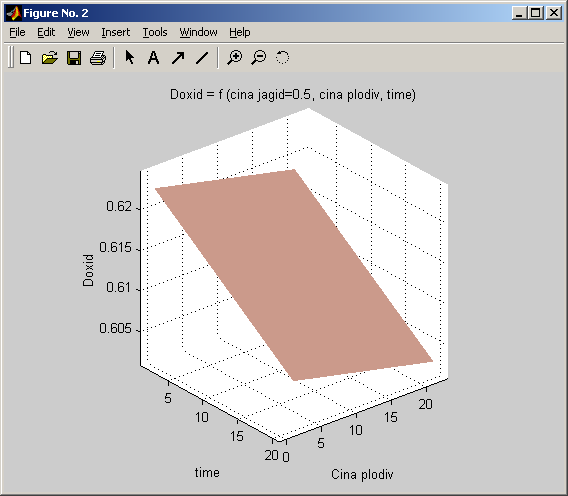
Рис. 1.17 – Проекція динамічного розв’язку на простір час – ціна овочів – дохід.

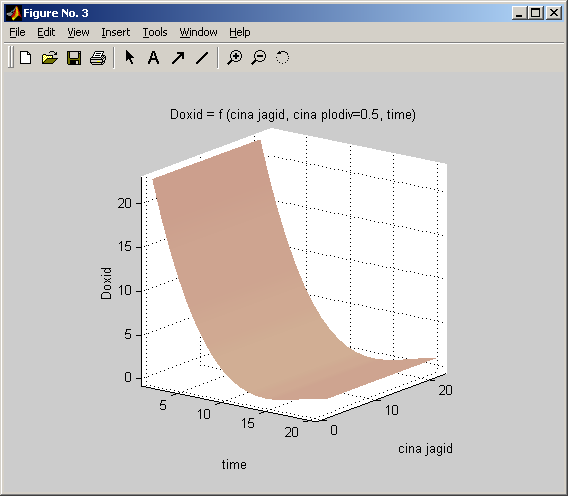
Рис. 1.18. Проекція динамічного розв’язку на простір час – ціна ягід – дохід.

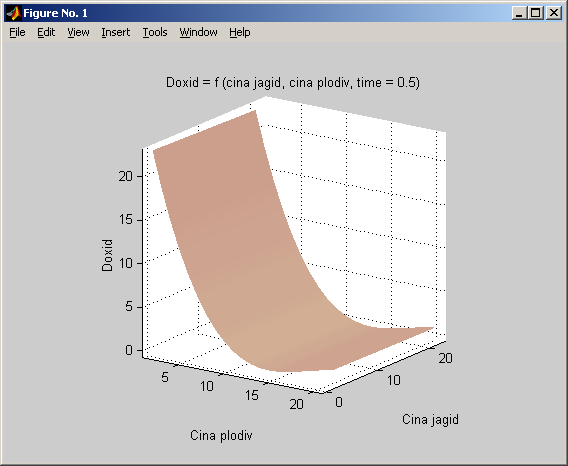
Рис. 1.19. Проекція динамічного розв’язку на простір ціна ягід – ціна овочів – дохід.

Як видно з проекцій розв’язків динамічної моделі при існуючій структури виробництва ніякі цінові впливи з сторони овочівництва не призводять до збільшення доходу плодоовочевого підприємства. Існує лише лінія найменших збитків (рис. 1.17).

Ціна овочів має оптимальну величину для дохідності плодоовочевого підприємства, що видно з мінімуму на рис. 1.19.

На модельованому відрізку часу виявлено найбільший спад дохідності, викликаний ціновими впливами аграрного та промислового ринків. Це видно з мінімуму на рисунку 1.18.

Як і в статичному випадку, в динамічній моделі, ціновий вплив ягідництва викликає прискорений ріст доходу. Ціновий вплив овочівництва залишається в рамках майже лінійно-пропорційного зв’язку з дохідністю.

Висновки. Для дослідження стану переробного плодоовочевого підприємства було вибрано групу величин, що відображають впливи аграрного та промислового секторів економки. Виконано попередній статистичний аналіз цих величин, який підтвердив відсутність статистичного кореляційного зв’язку між ними.

Для полегшення розв’язку некоректних ідентифікаційних задач часові ряди, вибрані для ідентифікації моделі, згаладжено з допомогою ковзного усереднення.

Визначено параметри лінійної регресійної моделі. На основі їх аналізу визначено групу чинників, які найсуттєвіше впливають на дохідність підприємства.

Для найістотніших факторів впливу на дохідність підприємства побудовано багатовимірну нелінійну статичну модель дохідності як функції зовнішніх чинників аграрного та промислового ринків. Для ідентифікації параметрів моделі застосовано метод найменших квадратів, з критерієм оптимальності, записаним з допомогою регуляризаційного функціоналу Тіхонова та з використанням редукції степеня апроксимаційного поліному.

З допомогою цього ж методу побудовано динамічну модель дохідності, в якій час заданий явно як аргумент багатовимірного степеневого полінома.

Виконано економічну інтерпретацію отриманих розв’язків моделі, встановлено ряд висновків щодо діяльності переробного підприємства в сучасних кризових умовах галузі.

Подано рекомендації щодо покращення роботи підприємства та вдосконалення державного регулювання в галузі садівництва та переробної плодоовочевої промисловості.

Практичне використання моделі веде до покращення економічного стану переробного підприємства, стабілізує його становище на ринку продуктів споживання й сприяє стійкому розвитку цього ринку, що має важливе соціальне значення, адже стосується якості харчового забезпечення основної частини громадян нашого суспільства.

Для розв’язання поставленої задачі – побудови моделі дохідності переробного підприємства за умов перехідної економіки вибрано метод регуляризованої реконструкції його виробничої функції, заданої багатовимірним степеневим поліномом, що зв’язує основні параметри, які впливають на діяльність підприємства.

Для визначення цих параметрів спершу побудовано концептуальну модель діяльності переробного підприємства в умовах глибокої кризи аграрного виробництва. На цій основі розроблено лінійну модель, що враховує численні фактори впливу на підприємство переробної галузі. Проведено якісний аналіз отриманих результатів. Виділено групу параметрів, що найсильніше впливають на переробне підприємство.

Для цього звуженого кола параметрів побудовано квадратичну алгебричну модель. На її основі виконано аналіз чутливості виробництва до зміни параметрів, що описують виробничий процес. Тобто, виконано модельне вирахування леверіджу як частинних похідних квадратичної апроксимації багатовимірної виробничої функції.

Для побудови алгебричної моделі дохідності переробного підприємства застосовано регуляризовані методи ідентифікації параметрів моделі, зокрема – метод комбінованої регуляризації з використанням стабілізуючого функціоналу Тіхонова та процедури пониження степені багатовимірного апроксимуючого полінома.

На основі математичного опису моделі розроблено програмне забезпечення мовою Matlab, в якому систему розроблено алгоритм регуляризованої ідентифікації параметрів моделі, записаної багатовимірним степеневим поліномом.

На основі названого програмного забезпечення проведено ряд обчислювальних експериментів з метою дослідження економічних тенденцій роботи плодоовочевого підприємства за існуючих економічних умов.