Технология выполнения работы

1. Запустить MS Excel и открыть чистый лист. Дать имя книге и сохранить файл (в дальнейшем не забывать периодически сохранять вносимые изменения).

2. Импортировать исходные данные из файла в область «Исходные данные» (рисунок 1.3) следующим образом:

–открыть файл с данными в новой книге;

Рисунок 1.3 – Расположение элементов на листе MS Excel при реализации метода Херста

–если необходимо, сделать соответствующие замены в формате данных, чтобы преобразовать их числовую форму (например, заменить точки, разделяющие целую и дробную части, на запятые);

–скопировать полученные и преобразованные данные в область «Исходные данные».

3. В область «Индексы данных» добавить порядковые номера исходных данных.

4. Построить график исходных данных с помощью мастера диаграмм и поместить его в одноименную область.

5. Используя мастер функций, определить объем исследуемых данных N и результат поместить в область «Выходные параметры».

6. Вычислить среднее арифметическое ряда X_ср используя формулу (1.1) и результат поместить в область «Выходные параметры».

7. Вычислить СКО ряда данных S по формуле (1.2) следующим образом:

–вычислить разность между каждым значением исходных данных и X_ср, результат поместить в область «Промежуточные данные для СКО» в столбец с заголовком «Хi- X_ср»;

–возвести в квадрат каждую из полученных разностей и результат поместить в область «Промежуточные данные для СКО» в столбец с заголовком «(Х_i- X_ср)^2»;

–используя мастер функций, вычислить значение S и результат поместить в область «Выходные параметры».

8. Определить точки (индексы данных), в которых будет вычисляться функция накопленного отклонения ряда от среднего по следующим правилам:

–на интервале индексов от 2 до 10 берутся точки с шагом 1;

–на интервале индексов от 10 до 100 берутся точки с шагом 10;

–на интервале индексов от 100 до 1000 берутся точки с шагом 100;

–на интервале индексов от 1000 до 10000 берутся точки с шагом 500;

–на интервале индексов от 10000 и более берутся точки с шагом 5000;

–точка с индексом N, т.е. последняя точка.

Выбранные индексы точек u фиксируются в строке «точки=u» области «Параметр Херста в точках».

9. Определяется среднее значение ряда на участках [1;u], где u – выбранные индексы точек, по формуле (1.3) и результат заносится в строку «X_срu» области «Параметр Херста в точках».

10. Находятся значения функции накопленного отклонения на участках [1;u] по формуле (1.3) и результат заносится в строки «Z₁», «Z₂» и т.д. области «Параметр Херста в точках».

Z₁=X₁- X_срu

Z₂=Z₁+X₂- X_срu

Z₃=Z₂+X₃- X_срu

………………..

Z_u=Z_u-1+X_u- X_срu

11. Используя мастер функций, находится максимальное и минимальное значения Z и определяется размах накопленного отклонения на соответствующем интервале по формуле (1.4). Результат заносится в строку «R_u» области «Параметр Херста в точках».

12. Определяется параметр Херста в точках u как отношение R_u/S. Результат помещается в строку «R/S» области «Параметр Херста в точках» для каждой точки u. Вычисляются десятичные логарифмы значений: точек u и R/S в этих точках. Результаты заносятся в область «Координаты точек для фрактальной плоскости».

13. Используя мастер диаграмм, вывести фрактальную плоскость метода Херста в одноименную область и изобразить линию тренда.

14. Вычислить угловой коэффициент аппроксимирующей линии тренда – k. Затем вычислить показатель Херста Н=k-1 и результат поместить в область «Выходные параметры».

Коэффициент k находится по методу наименьших квадратов следующим образом. Пусть имеется ряд точек с координатами (x₁;y₁), (x₂;y₂), … ,(x_i;y_i), … ,(x_n;y_n), которые аппроксимируются линейной зависимостью, описываемой уравнением:

Y_p=kX_p+b.

Тогда коэффициенты данного уравнения линейной зависимости находятся как:

;

.

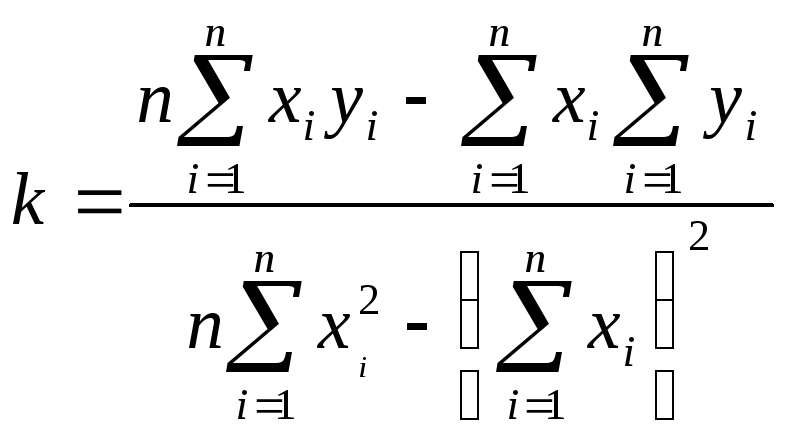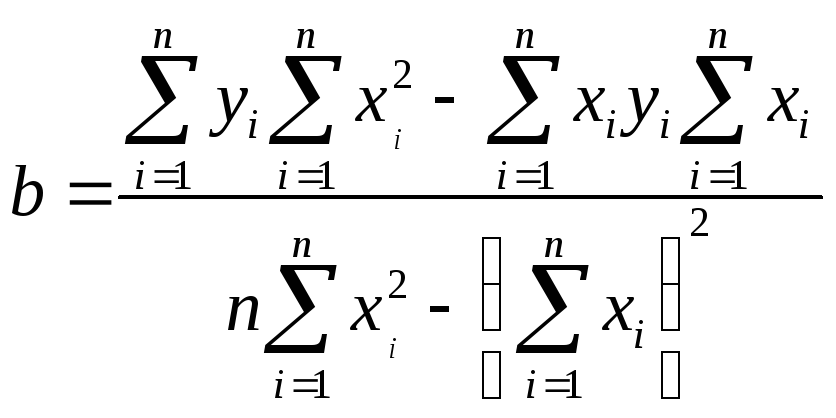15. Вычислить фрактальную размерность D по формуле (1.6) и результат поместить в область «Выходные параметры».

16. Вычислить степень долговременной корреляции С по формуле (1.7) и результат поместить в область «Выходные параметры».

17. Проверить правильность реализации метода Херста, путем определения Н у рядов с известными фрактальными свойствами (таблица 1.2).

Таблица 1.2

Названия файлов, содержащих эталонные данные

Нт	0.1	0.5	1
Имя файла	etalon.h01	etalon.h05	etalon.h1

Оценить погрешность нахождения Н по формуле:

γ=(Н-Н_т)/H_т*100%,

где Н – экспериментальный показатель Херста,

Н_т – теоретический показатель Херста.

Погрешность не должна превышать 20%, в противном случае необходимо пересмотреть реализацию метода Херста.

18. Определить фрактальные характеристики данных из других файлов.

19. Составить отчет о проделанной работе в MS Word.