Окружность и круг

Пусть - длина радиуса некоторого круга, - длина окружности этого круга и - его площадь. Тогда , .

Угол между двумя радиусами окружности называется центральным углом. Если - радианная мера центрального угла, то длина дуги окружности равна ,

площадь центрального сектора равна ,

площадь сегмента равна .

Угол, образованный двумя хордами, исходящими из одной точки окружности, называется вписанным углом. Величина вписанного угла равна половине центрального угла, опирающегося на ту же дугу окружности. Следствие: углы, опирающиеся на диаметр – прямые. Вписанные углы, опирающиеся на одну и ту же длину окружности, равны между собой.

Касательные, проведенные к окружности из одной ее точки, имеют одинаковую длину, а центр окружности находиться на биссектрисе угла, образованного этими касательными. Радиус, проведенный в точку касания, перпендикулярен касательной.

Если хорды и окружности пересекаются в точке , то .

Если из точки к окружности проведены две секущие, пересекающие ее в точках , и , соответственно, то .

Радиус окружности, описанной вокруг правильного многоугольника ( - количество сторон многоугольника, - длина стороны), определяется формулой:

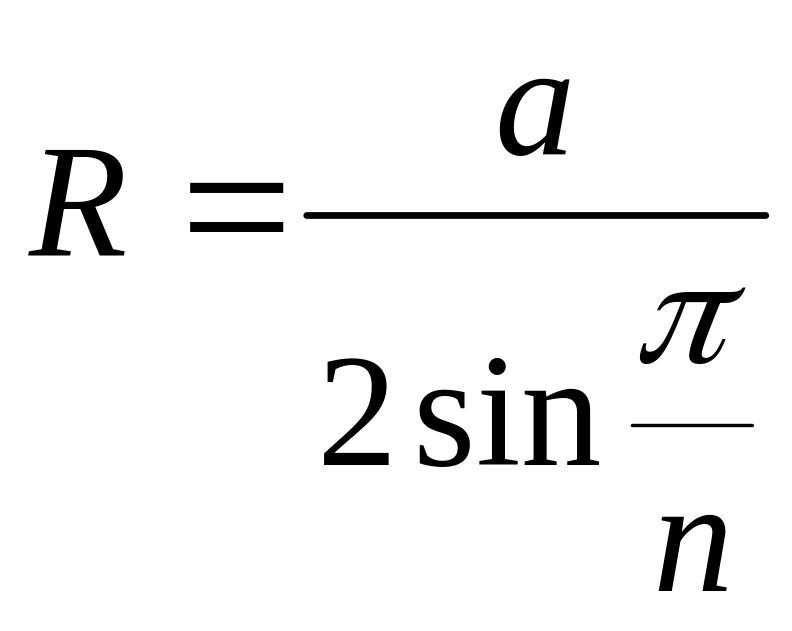, описанной вокруг правильного многоугольника: .

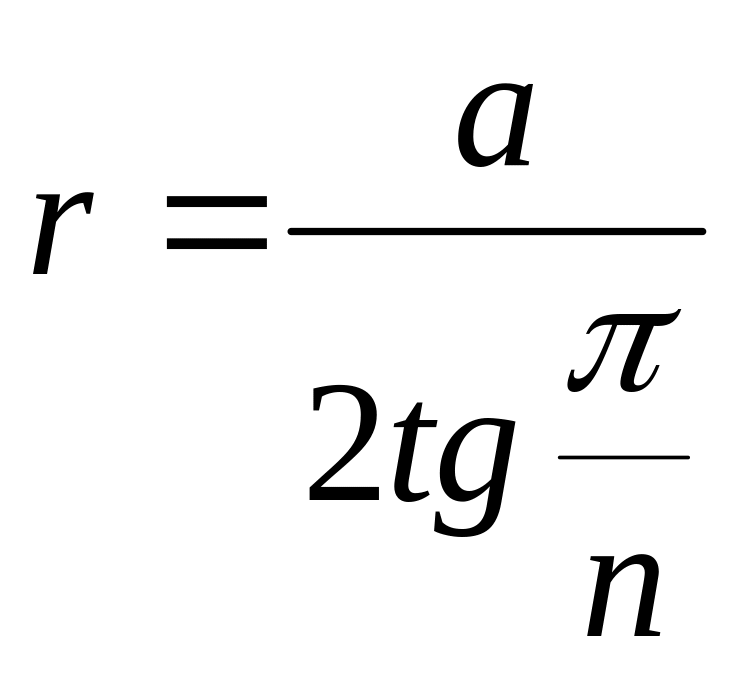Многоугольники

Длина ломанной не меньше отрезка соединяющего ее концы.

Сумма внутренних углов выпуклого -угольника равна . Сумма внешних углов выпуклого -угольника, взятых по одному при каждой вершине, равна .

Правильный выпуклый многоугольник является вписанным в окружности и описанным вокруг окружности. Правильные выпуклые -угольники подобны. В частности, если у них стороны равны, то они равны. Следствие: у правильных -угольников отношения периметров, радиусов вписанных и описанных окружностей равны.

Дополнительные соотношения

Т реугольник