
- •75. Основы теории спектроскопии ямр: магнитные и спиновые характеристики ядра, магнитный момент ядра и его взаим-вие с магнитным полем, расщепление энергетических уровней ядра в магнитном поле.
- •78. Магнито-эквивалентные и магнито-неэквивалентные ядра, сверхтонкая структура спектров ямр, мультиплетность сигналов в спектре в ямр, константа спин-спинового взаимодействия.
- •79. Правила интерприт. Сверхтонк. Ст-ры в спектрах, завис. Спин-спинов. Взаим. От ст-ры, связь хим. Сдвига и констант спин-спин. Взаим. Со стр. Молек.
- •80. Общая схема по ямр: треб. К оборуд. Услов. Провед. Стац. Метода (развертка по полю и частоте)
- •82 Теоретические основы спектроскопии электронного парамагнитного резонанса, условия эпр, положение резонансного сигнала. Электрон-ядерное взаимодействие и сверхтонкая структура спектра эпр.
- •83. Методы квадрупольного и гамма резонанса: основы метода, техника эксперимента. Практическое применение.
75. Основы теории спектроскопии ямр: магнитные и спиновые характеристики ядра, магнитный момент ядра и его взаим-вие с магнитным полем, расщепление энергетических уровней ядра в магнитном поле.
ЯМР-С – в основе лежит явл резонансного поглощения ЭМИ радиочастотного диапазона (длина волны > 1) ядрами атомов вещества, помещённого в постоянное магнитное поле (МП). Открыт в 1945г - Блох, Перселл
Преимущества:1)экспрессность; 2)высокая чувств-сть; 3)неразрушающий метод контроля (10-5 г) Недостатки: 1)высокая стоимость прибора; его габариты 2)эксплуатация. Применение метода: 1)установление структуры хим. соединений; 2)изучение динамики хим. реакций; 3)проведение кач-го и колич-го анализа сложных смесей органических соединений. Объекты исследования: вещества, содержащие атомы, ядра которых являются магнито-активными.
Атомное ядро состоит из протонов и нейтронов, каждый из них имеет собственный спин = ½. Вел-на рез-щего спина ядра(j) опр-тся числом протонов и нейтронов, т.е. связана с такими хар-ами ядра как его заряд (поряд № элемента) = количеству протонов и массовое число (сумма масс протонов и нейтронов).
Массовое число |
нечётн. |
чётн. |
чётн. |
Атомное число |
чётн. или нечётн. |
чётн. |
нечётн. |
Результ. ядерный спин j |
½, 3/2, 5/2 |
0 |
1,2,3 |
Примеры |
1Н, 13С - ½ Cl35 -3/2, 12О -5/2 |
12С 16О ядра магнитонеактивные |
2Н, 10В |
Если ядро имеет j=0, его результирующий угловой момент количества движения Р=0, определяемый в квантовой механике, как Р = ( ћ/ 2 π )* j = h*j (ћ – постоянная Планка) .Такое ядро явлмагнитонеактивным, т.к. оно хоть и явл электрозаряженной частицей, состоящих из вращающихся вокруг своих осей протонов и нейтронов имеют результирующее МП=0.
Ядро, имеющее j ≠0, как электрически заряженная частица вращающаяся вокруг некоторой оси создаёт собственное маг поле и хар-ется магн моментом μn, величина которого пропор-на угловому моменту кол-ва движения Р: μn =γnР, где γn - коэффициент пропорциональности, называемый гиромагнитным или магнитомеханическим отношением коэффициента ядра.
Т.к.
Р=
ћ
*j , то μn
= γn
ћ
*j В зависимости от направления вращения
ядра его магнитный момент может быть
положительным (+n)
или отрицательным (-n).
В
отсутствие
внеш магн поля любые ориентации
ядерногомагнитного момента равновероятны,
т.е. квантовые спиновые состояния ядра
вырождены.
Ядро с угловым моментом P
и магн моментом n
в статическом магн поле B0
ведет себя так, что располагающийся
вдоль магнитного поля компонент
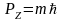 ,
где m
– магнитное квантовое число, которое
принимает значения I,
I-1,
…, -I+1,
-I.
Очевидно,
что m
может принимать (2I+1)
различных значений и, соответственно,
для углового и магнитного моментов м
набл-ться
аналогичное число возможных ориентаций
(квантование по направлению) (рис.1).
,
где m
– магнитное квантовое число, которое
принимает значения I,
I-1,
…, -I+1,
-I.
Очевидно,
что m
может принимать (2I+1)
различных значений и, соответственно,
для углового и магнитного моментов м
набл-ться
аналогичное число возможных ориентаций
(квантование по направлению) (рис.1).
Магнитный момент ядра м.б. выражен ядерный g-фактор, который = произведению безраз-ой постоянной gn и ядерного магнетона n.
n =(еђ)/ (2 mnc)=5,0510-27A·м2
е- заряд протона; с – скорость света в вакууме; mn - масса протона; n – магнитный момент протона (ядерный магнетон Бора). Магнитный момент ядра выражается через ядерный g-фактор μn = n j gn.
Значение μn, j, gn. и γn явл табулированными хар-ками ядра, т.к. зависят от его природы. При наложении на систему магнитоактивных ядер постоянного МП, между μn и внеш МП возникает взаим-вие, пропорциональное напряжённости Н, налагаемого внеш поля, и зависит от ориентации вектора магн момента ядра относительно направления внешнего МП. Вел-на энергии взаим-вия квантована, т.е. возможен только некоторый дискретный набор сост, в котором система находится в стационарных состояниях с энергией Еi. Этот набор опр-тся магнитным квантовым числом mI, которое может принимать 2j+1,т.е. от +j до –j. Н-р, у протона или другого ядра с j=1/2 возможно только 2 значения магн квантового числа (+1/2; -1/2) и только 2 стац-ых разрешённых спиновых сост-ий с Е1 и Е2 при этом Е1= - μn Н = -1/2 γn ђ Н = -1/2 gn n Н
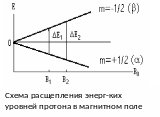
Е2= + μn Н = +1/2 γn ђ Н = +1/2 gn n Н Т.о. в постоянном МП происходит т.н. эффект Зеемана -расщепление энерг уровня ядер со спином j=1/2 на 2 подуровня. Количество ядер, находящихся при данных условиях в МП в равновесии в определ спиновых сост-ях т.н. равн-ная заселённость спиновых состояний определ з-ом Больцмана. (n2/n1) = e -∆E/kT
n1-количество частиц в энергетическом состоянии Е1, n2 - количество частиц в энергетическом состоянии Е2. Получения ЯМР- спектра избыток заселённости нижнего уровня. Чем больше напряжённость, тем больше разность заселённости уровней Е1 и Е2. Переходы между энергетическими уровнями, сопровождающимися изменениями энергиями системы могут происходить при удовлетворении всех спектральных методах условия: ∆Е= hν.Т.е. они м происходить с исп-ием или погл-ием излучения частоты ν. При одинаковой заселённости уровней сигналы ЯМР не наблюдаются.
76. Условия ЯМР: основное уравнение резонанса, частота прецессии ядер, бвращающаяся система координат, резонанс изолированного ядра, уравнение Блоха, релаксационные процессы в образце, ширина линии в спектре ЯМР.
Условия ЯМР: Магнитоактивное ядро, Наличие пост магн поля.
Для возбуждения переходов между энерг уровнями на образец, помещённый в постоянное МП(однородное) необходимо воздействовать переменным МП напр-стью Нν , сравнимы по энергии с разностью ∆Е уровней энергии ядер, по которым они распределялись в постоянном МП. Резонансное поглощение происходит только при условии, что вектор переменного МП перпендикулярен вектору постоянного МП и удовлетворяется условие
hν = γn ћ Н = gn n Н - условие ЯМР Н- напр-сть внеш пост МП; ν – частота переменного э/м поля.
Частота прецессии ядер ∆Е=γ*h/2π*B0, ∆Е= hν след-но ν= γ/2π*B0, ω= γ*B0
Е сли
суммарная намагниченность расположена
в плоскости XY, она будет вращаться вокруг
оси Z с частотой, равной частоте фотона,
который вызывает переход между двумя
энергетическими уровнями спина. Эта
частота называется частотой
Лармора-прецессия.
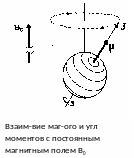
Магнитные
св-ва
ядер
J
– момент кол-ва
движения,
µ
– магн
момент ядра,
B0
– магнитное
поле
сли
суммарная намагниченность расположена
в плоскости XY, она будет вращаться вокруг
оси Z с частотой, равной частоте фотона,
который вызывает переход между двумя
энергетическими уровнями спина. Эта
частота называется частотой
Лармора-прецессия.
Магнитные
св-ва
ядер
J
– момент кол-ва
движения,
µ
– магн
момент ядра,
B0
– магнитное
поле
Прецессия ядра, обладающего магнитным моментом в магнитном поле
При резонансном поглощении энергии переменным э/м поля магнитный момент ядра меняет своё направление на противоположное, и поглощаемая при этом энергия фиксируется в виде сигнала ЯМР.
Резонанс изолированного ядра

![]()

![]()
Рис. Состояние резонанса

В точке резонанса во вращающейся системе координат векторы m и В1 неподвижны. Это означает, что при резонансе в системе X’Y’Z’ нет прецессии m вокруг В0. Возможен переворот (прецессия) вокруг В1
 Рис.
Поведение суммарного вектора
намагниченности
Рис.
Поведение суммарного вектора
намагниченности
![]() двух
магнитных полей: постоянного и
вращающегося с частотой ларморовой
прецессии.
двух
магнитных полей: постоянного и
вращающегося с частотой ларморовой
прецессии.

Восстановление суммарной намагниченности до исходного значения релаксации характеризуется 2-мя временами T1 и Т2.
Ф-ция распределения по осям Mx(t)=- Mx/T2; My(t)= )=- My/T2; Mz(t)=-1/T1*Mz-M0.
Рис. Вектор намагниченности М0

dM/dt=yM×H- уравнение Блоха
dMx/dt=y(MyH0+MzH1sinωt)
dMy/dt=y(MzH1cosωt-MxH0)
dMz/dt=-y(MxH1sinωt+MyH1cosωt)
Данные ф-лы показ-т, как измен-ся вектор суммарной намагниченности образца в процессе резонанса. Конечные ур. Блоха:
dMx/dt=y(MyH0+MzH1sinωt)-Mx/T2
dMy/dt=y(MzH1cosωt-MxH0)-My/T2
dMz/dt=-y(MxH1sinωt+MyH1cosωt)-((Mz-M0)/T1)
M0- нулевая намагниченность
Рис. Прецессия М в неподвижной системе координат

Рис. Движение вектора M во вращающейся системе координат С' в момент прохождения через резонансные условия.

Т1- время спинрешёточной (продольной релаксации), хар-ет взаим-вие магн моментов ядер с ь.н. решёткой остальным в-вом Продольная релаксация связана с передачей энергии ядер окруж среде и превр-ем её в тепловую энергию системы. За счёт спин-решёточной релаксации поддерж-тся Больцмановское распр-ние засел уровней.
Т1 зависит от: 1)типа ядер, 2)молекулярного движения.
Обычно сигнал достигнув за некоторое время максимального значения со временем не изменяет интенсивность – это происходит благодаря безызлучательным переходам, приводящим к потере энергии ядрам на верхнем уровне и вследствие возвращение на нижний уровень. Такой процесс называется релаксационным. Связь резонирующих ядер с решёткой осуществляется через различные взаимодействия:
Диполь-дипольное магн взаим-вие- определяет основную ширину сигнала. Явл источником сильного переменного электромагнитного поля в различных жидкостях и газах, где ядра вкл-ны в быстрое тепловое движение. Вклад этого взаимод-я в спин-решёточную релаксацию, чем ближе друг к другу магнитные ядра молекул.
Скалярно спин-спиновое взаимод-е-передаётся от ядра к ядру с помощью электронов и не зависит от пространственной ориентации молекулы. Вклад данного взаимод-я сущ-но меняется при изменении хар-к хим. связей в молекуле.
При столкновении молекул в процессе теплового движ-я меняется ориент-ция суммарного молекулярного магнитного момента, меняется локально-магнитное поле на молекуле. Это спин-вращательное взаимод-е Квадрупольное(?)-хар-но для ядер, у которых спин превышает 1/2. Время Т2- время спин-спиновой(поперечной) релаксации, закл-ся в обмене энергией м/у спинами ядер одного типа. Она не отражается на заселённости энерг уровней. В простейших случаях для ж-тей Т1=Т2. При этом после после резонанса скорость исчезновения х,у- компоненты намагниченности совпадает со скоростью восстановления продольной намагниченности вдоль оси z.
В плоскости ху осущ-ся перераспределение энергии м/у ядрами за счёт ЭИвзаимодействий.
Связь времён релаксации с шириной линии спектра ядерного магнитного резонанса
∆ ν≈1/πτ +σ ν
∆ ν≈1/πТ2 +σ ν, т.к Т2<Т1, это приводит к спин-спиновому взаимодействию.
Оба типа релаксационных процессов зависят:
- времени жизни ядер на верхних энергетических уровнях и определяют ширину спектральных линий. В твёрдых телах возникают широкие спектральные линии и спектроскопию ЯМР твёрдых тел называют – называют спектроскопией ЯМР широких линий. Такой спектр представляет собой набор широких полос поглощения соответствующей частоты. В подвижных жидкостях условия резонанса зависят от слабых локальных магнитных полей, связанных со структурой молекул. Эти небольшие эффекты могут регистрироваться приборами с высокой разрешающей способностью.
Из основного уравнения резонанса может быть достигнута 2 путями – или изменением частоты переменного э/м поля ν при постоянной напряжённости постоянного МП (частотная развёртка) или изменением напряжённости при ν = const это т.н. полевая развёртка. В большинстве современных спектрометров ЯМР обычно используется полевая развёртка спектра.
77. Экранирование ядра электронами, константа экранирования ядра, межмолекулярное взаимодействие. Абсолютный и относительный химический сдвиг, шкалы химических сдвигов, зависимость химического сдвига от структуры.
Наиболее часто рассматриваются спектры полученные на ядрах водорода.
Ядра водорода в органических молекулах окружены электронами. Вращение электронов создает свое поле, которое накладывается на внешнее поле, действующее на ядро. Т.е. электроны заслоняют (экранируют) ядро от внешнего магнитного поля, поэтому напряженность поля около ядра отличается от напряженности внешнего магнитного поля. В результате изменения магнитного экранирования изменяется частота вращающегося поля, при которой наблюдается явление резонанса. Это изменение называется химическим сдвигом. Химический сдвиг определяется положением данного протона в молекуле. Для эквивалентных протонов значение химического сдвига одинаково, и они дают один резонансный сигнал. Различающиеся окружением в молекуле протоны обладают разными химическим сдвигами и дают раздельные сигналы.
В настоящее время в качестве международного стандарта для измерения химических сдвигов В ПМР- спектроскопии используют тетраметилсилан (ТМС), который имеет интенсивный узкий сигнал протонов в более сильном поле, чем протоны в большинстве веществ.
Хим. сдвиг = (Н образца – Н эталона) 106/Н =(ν образца – ν эталона) 106/ ν
где Н образца, Н эталона – это напряжённости постоянного магнитного поля при резонансе магнитоактивных ядер в спектре образца или эталона соответственно; Н – рабочая напряжённость постоянного магнитного поля прибора; ν образца, ν эталона – частоты поглощения образца и эталона
соответственно.
В ЯМР применяется две шкалы хим. сдвигов σ и шкалы. В шкале σ за 0 принимается положение сигнала ТМС и хим. сдвиги увеличиваются в сторону слабого поля. В шкале положение сигнала принято за 10 м.д. и
соответственно = 10 – σ м.д.. Значение хим. сдвигов в шкале увеличиваются в сторону сильного поля. Чтобы перейти от величин хим. сдвигов в Гц к шкале σ следует пользоваться формулой:
σ = (ν образца – ν ТМС) 106/ ν , при этом ν ТМС = 0
Значение хим. сдвигов по σ и шкалах не зависят от рабочих характеристик используемого спектра ЯМР. Если ядра одной молекулы имеют одинаковые хим. сдвиги и химически равноценны, то они называются химически эквивалентными ядрами.
На величину хим. сдвига оказывает влияние ближайшее окружение резонирующего ядра. Такое влияние окружения расширяет применение ЯМР спектроскопии как метода изучения структуры молекулы.
