10. Теорема о единственности предела

Как мы говорили с Вами в прошлой статье, единственность предела следует из определения предела функции по Гейне. Однако давайте сформулируем и докажем теорему о единственности предела.

Теорема о единственности предела Формулировка:

Если функция  в точке  имеет предел, то этот предел единственный.

Доказательство:

Докажем методом от противного. Предположим, что , , . Возьмём , по определению и свойству окрестности найдётся такая проколотая   -окрестность точки  ( ), в которой одновременно будут выполнятся неравенства ,  , тогда в точках этой же окрестности  Получили противоречие . Отсюда, функция  в точке  имеет единственный предел.

6. Теорема о необходимом условии сходимости числовой последовательности.

Теорема. Если монотонная последовательность  ограничена, то она сходится.

Доказательство. Так как последовательность  ограничена, то множество ее элементов имеет точные верхнюю  и нижнюю  грани. Пусть  – неубывающая последовательность и – точная верхняя грань множества ее элементов. Это означает, что для любого числа  можно указать такой элемент , что  и . Эти два неравенства равносильны неравенству  или . Так как  – неубывающая последовательность, то при  выполняется  или . Это означает, что при  выполняется  или . Таким образом, . Аналогично доказывается случай, когда  – невозрастающая последовательность.

Замечание 1. Условие ограниченности монотонной последовательности представляет собой необходимое и достаточное условие ее сходимости. Действительно, по теореме 8 сходящаяся монотонная последовательность ограничена.

Замечание 2. Сходящаяся последовательность может и не быть монотонной. Например, последовательность  сходится к числу ноль, но не является монотонной.

Замечание 3. Если последовательность  неубывающая сходящаяся и - ее предел, то для всех номеров n выполняется неравенство . Аналогично, если  невозрастающая сходящаяся последовательность и  – ее предел, то для всех номеров n справедливо .

6. Свойства сходящихся последовательностей, связанные с арифметическими действиями и неравенствами.

Последовательность {x_n} называется ограниченной снизу (сверху), если существует такое число C, что все члены последовательности удовлетворяют условию x_n ≥ C (x_n ≤ C). Последовательность, ограниченную как сверху, так и снизу, называют ограниченной.

Рисунок 1.1.2.1. Последовательность называют ограниченной, если C1 ≤ xn ≤ C2.

Геометрически ограниченность последовательности означает, что все ее значения лежат на некотором отрезке.

Можно показать, что если последовательность имеет предел, то она ограничена.

Заметим, что не всякая ограниченная последовательность является сходящейся. Примером расходящейся ограниченной последовательности может служить последовательность {x_n}: x_n = (–1)ⁿ.

Т еорема о трех последовательностях. Если последовательности {x_n}, {y_n}, {z_n} таковы, что x_n ≤ y_n ≤ z_n для всех n ≥ N, и

то последовательность {y_n} сходится, и

Если  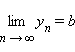 и для любого      то a ≥ b.

Любая неубывающая ограниченная сверху последовательность сходится.

Любая невозрастающая ограниченная снизу последовательность сходится.

Суммой, разностью, произведением и частным двух последовательностей {x_n} и {y_n} называют соответственно последовательности {x_n + y_n}, {x_n – y_n}, {x_n ∙ y_n}, {x_n / y_n}. При определении частного предполагается, что y_n ≠ 0 при всех n.

Справедлива следующая теорема (основная теорема теории пределов): если 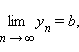  то:

• ;

• ;

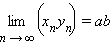• при условии, что b ≠ 0 и 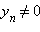для всех n.

Последовательность {α_n} называется бесконечно малой, если

Если число a – предел последовательности {x_n}, то последовательность {α_n}, где α_n = x_n – a, бесконечно малая. Примером бесконечно малой последовательности является геометрическая прогрессия {qⁿ}, где |q| < 1.

• Произведение бесконечно малой последовательности на ограниченную последовательность есть бесконечно малая последовательность.

• Из определения бесконечно малой последовательности непосредственно следует, что алгебраическая сумма конечного числа бесконечно малых последовательностей есть бесконечно малая последовательность. Заметим, что конечность числа бесконечно малых последовательностей в этой алгебраической сумме существенна.

• Произведение конечного числа бесконечно малых последовательностей есть бесконечно малая последовательность. Заметим, что и здесь конечность числа последовательностей также существенна, т. к. произведение бесконечного числа бесконечно малых последовательностей может уже и не быть бесконечно малой последовательностью.

Множества и называются δ-окрестностями –∞ и +∞ соответственно.

Определим понятие бесконечного предела. Говорят, что 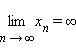, если для любого R > 0 существует такой, что при

Последовательность {x_n} называется бесконечно большой, если

Другими словами, , если для любого δ > 0 найдется номер такой, что для любого    Аналогично вводятся понятия бесконечных пределов +∞ и –∞. Примерами бесконечно больших последовательностей могут служить {n²} или {1 – n}.

Рисунок 1.1.2.2. δ-окрестность +∞