
- •Постоянные и переменные величины
- •Множества, операции над множествами. Символика математической логики.
- •Элементы логической символики
- •Действительные числа и их свойства
- •Понятие окрестности точки. Точки прикосновения, предельные, граничные и внутренние точки множества.
- •5. Открытые и замкнутые множества. Отрезок, интервал, промежуток действительной прямой. Ограниченные множества.
- •Понятие отображения (функции). Образы и прообразы множеств
- •Способы задания функций. Обратная функция, сложная функция.
- •Числовые последовательности.
- •Предел последовательности
- •Определение предела последовательности
- •Ограниченные и монотонные последовательности.
- •Примеры исследования последовательности на ограниченность
- •10. Теорема о единственности предела
- •Теорема о единственности предела Формулировка:
- •Доказательство:
- •Теорема о необходимом условии сходимости числовой последовательности.
- •Свойства сходящихся последовательностей, связанные с арифметическими действиями и неравенствами.
- •Предел функции
- •Свойства пределов функции, связанные с арифметическими действиями и неравенствами.
- •Предел сложной функции
- •Односторонние пределы
- •Предел монотонной функции
- •Теорема о существовании односторонних пределов у монотонных функций Формулировка:
- •Доказательство:
- •18. Бесконечно большие, бесконечно малые и эквивалентные величины
- •Бесконечно малая
- •Бесконечно большая величина
- •Свойства бесконечно малых и бесконечно больших
- •Теорема
- •Примеры использования
- •19. Основные виды неопределенностей
- •20. Замечательные пределы
- •21. Непрерывность функции в точке и на множестве. Арифметические операции с непрерывными функциями
- •22. Свойства функций, непрерывных на отрезке и 23. Основные теоремы о функциях, непрерывных на отрезках
- •24. Точки разрыва и их классификация
- •Точка разрыва первого рода
- •Точка разрыва второго рода
- •Точка устранимого разрыва
- •25. Производная и дифференциал функции. Связь с непрерывностью.
- •26. Геометрическое и механическое истолкование производной Геометрический смысл производной
- •Механический смысл производной
- •27. Геометрический смысл дифференциала
- •28. Дифференцируемость функции, необходимые и достаточные условия дифференцируемости
- •29. Таблица производных и дифференциалов основных элементарных функций.
- •30. Производная и дифференциалы суммы, произведения частного.
- •Производная сложной функции и обратной функции
- •Производные высших порядков
- •Механическое истолкования второй производной
- •Дифференциалы высших порядков
- •Признаки постоянства, возрастания и убывания функции на промежутке.
- •Нахождение максимумов и минимумов функции с помощью производных.
- •Нахождение наименьших и наибольших значений функции на замкнутом промежутке
- •Правило раскрытия неопределенности Лопиталя-Бернулли
- •Касательная к плоской кривой. Выпуклость и вогнутость плоской кривой
- •40.Точки перегиба графика функции на основе ее полного анализа
- •Первое достаточное условие перегиба.
- •Асимптоты
- •Построение графика функции на основе ее полного анализа
- •Первообразная функция. Неопределенный интеграл и его основные свойства
- •Основные методы интегрирования
- •I. Метод непосредственного интегрирования
- •II. Метод подстановки (интегрирование заменой переменной)
- •III. Метод интегрирования по частям
Построение графика функции на основе ее полного анализа
Провести полное исследование функции и построить её график
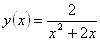
Решение.
1) Область определения:
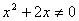 или
или
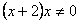 , то есть
, то есть
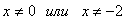 .
.
 .
.
Таким образом:
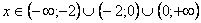 .
2) Точек
пересечения с осью Ox нет. Действительно,
уравнение
.
2) Точек
пересечения с осью Ox нет. Действительно,
уравнение
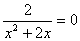 не имеет решений.
Точек
пересечения с осью Oy нет, так как
не имеет решений.
Точек
пересечения с осью Oy нет, так как
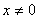 .
3) Функция
ни чётная, ни нечётная. Симметрии
относительно оси ординат нет. Симметрии
относительно начала координат тоже
нет. Так как
.
3) Функция
ни чётная, ни нечётная. Симметрии
относительно оси ординат нет. Симметрии
относительно начала координат тоже
нет. Так как
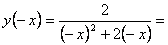
 .
.
Видим, что
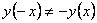 и
и
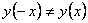 .
4) Функция
непрерывна в области определения
.
4) Функция
непрерывна в области определения
.
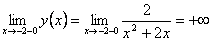 ;
;
 .
.
Следовательно, точка
 является точкой разрыва второго
рода (бесконечный разрыв).
является точкой разрыва второго
рода (бесконечный разрыв).
 ;
;
 .
.
Следовательно, точка
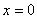 является точкой разрыва второго
рода (бесконечный разрыв).
5)
Вертикальные асимптоты:
является точкой разрыва второго
рода (бесконечный разрыв).
5)
Вертикальные асимптоты:
 Найдём наклонную асимптоту
Найдём наклонную асимптоту
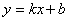 . Здесь
. Здесь
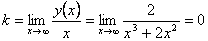 ;
;
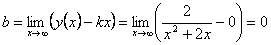 .
.
Следовательно, имеем горизонтальную асимптоту: y=0. Наклонных асимптот нет. 6) Найдём первую производную. Первая производная:
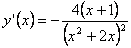 .
.
И вот почему
 .
.
Найдём стационарные точки, где производная равна нулю, то есть
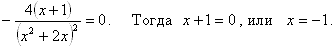 .
.
7) Найдём вторую производную. Вторая производная:
 .
.
И в этом легко убедится, так как
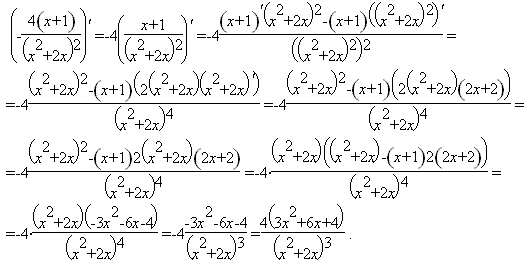 .
.
Найдём точки перегиба графика функции , в которых вторая производная обращается в ноль. То есть

Тестовые интервалы:

Результаты исследования функции занесем в таблицу.
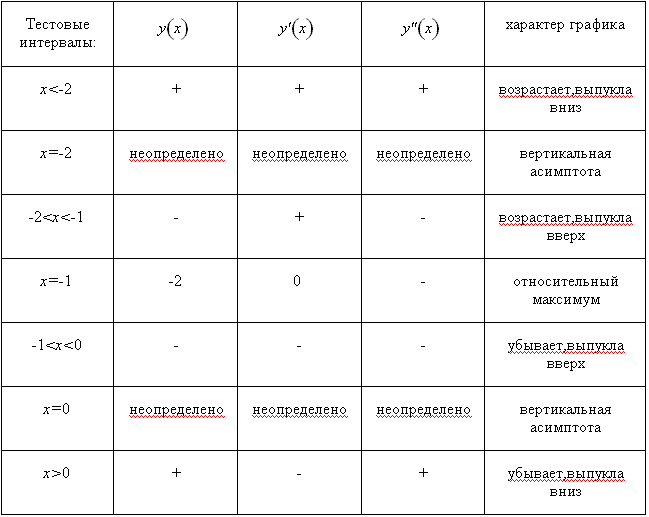 Относительный
максимум (-1;-2).
8) Данные таблицы нанесем на координатную
плоскость. Используя результаты
исследования
функции, построим ее график.
Относительный
максимум (-1;-2).
8) Данные таблицы нанесем на координатную
плоскость. Используя результаты
исследования
функции, построим ее график.


Посмотрите бесплатные решения из других разделов задачника Кузнецова Л.А.
1 Пределы
2 Производные
3 Графики
4 Интегралы
5 Дифференциальные уравнения
6 Ряды
7 Кратные интегралы
8 Векторный анализ
9 Аналитическая геометрия
10 Линейная алгебра
11 Уравнения математической физики
Первообразная функция. Неопределенный интеграл и его основные свойства
Первообразная функция данной функции f(x) – такая функция F(x), производная которой на данном промежутке равна f(x). Отыскание первообразной функции – операция, обратная дифференцированию, ее называют также интегрированием. Эта операция неоднозначна – для данной интегрируемой функции f(x) существует бесконечно много первообразных, но каждые две из них отличаются на константу. Совокупность всех первообразных функций называется неопределенным интегралом от f(x). Обычно ее записывают в виде F(x) = Ф(х) + С, где Ф(х) – какая-нибудь первообразная (все равно какая), а С – произвольная постоянная величина.
Если функция f ( x ) имеет первообразную на промежутке X, и k – число, то
![]()
Короче: постоянную можно выносить за знак интеграла.
Если функции f ( x ) и g ( x ) имеют первообразные на промежутке X , то
![]()
Короче: интеграл суммы равен сумме интегралов.
Если функция f ( x ) имеет первообразную на промежутке X , то для внутренних точек этого промежутка:
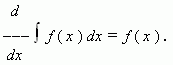
Короче: производная от интеграла равна подынтегральной функции.
Если функция f ( x ) непрерывна на промежутке X и дифференцируема во внутренних точках этого промежутка, то:
![]()
Короче: интеграл от дифференциала функции равен этой функции плюс постоянная интегрирования.
Таблица неопределенных интегралов от основных элементарных функций.

