26. Геометрическое и механическое истолкование производной Геометрический смысл производной

Пусть функция определена в некоторой окрестности токи , непрерывна в этой точке и , а (рис.2).

Рис. 2

Придав произвольное приращение аргументу , так чтобы , перейдем к точке с абсциссой и ординатой , где .

Уравнение прямой, проходящей через точки и (секущей графика функции , имеет вид: , где отношение представляет собой угловой коэффициент секущей ( .

Касательной к графику функции в точке называется предельное положение секущей , при стремлении точки по графику к точке .

Для того, чтобы секущая при стремилась к предельному положению, отличному от вертикальной прямой , необходимо и достаточно, чтобы существовал конечный предел , то есть , чтобы существовала конечная производная функции в точке .

Угловой коэффициент касательной получается путем перехода от к пределу при :

Таким образом, получим, что , где - угол наклона касательной к оси (см. рис.), а значение производной равно угловому коэффициенту касательной к графику функции. В этом заключается геометрический смысл производной. Уравнение касательной к графику функции в точке имеет вид

В случае бесконечной производной .

Из уравнения секущей имеем:

Переходя в равенстве к пределу при , получаем уравнение касательной к графику функции в точке в виде , то есть касательная является в данном случае вертикальной прямой, проходящей через точку оси абсцисс.

Механический смысл производной

Пусть материальная точка движется прямолинейно и - длина пути, проходимого за время , отсчитываемого от некоторого момента времени .

Для определения скорости в данный момент придадим переменной некоторое приращение , при этом приращение пути будет равно .

Отношение называется в физике величиной средней скорости движения за промежуток времени, начиная с момента времени , и обозначается

Предел называется величиной мгновенной скорости движения в момент времени .

Таким образом, мгновенная скорость в момент времени прямолинейного движения, совершаемого по закону равна значению производной .

27. Геометрический смысл дифференциала

 

Н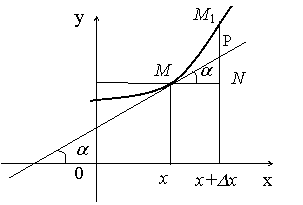 а графике функции возьмем произвольную точку и дадим аргументу приращение . При этом функция получит приращение (на рисунке отрезок ).

Проведем касательную к кривой в точке и обозначим угол ее наклона к оси через , тогда . Из треугольника находим , т.е. .

Таким образом, дифференциал функции численно равен приращению ординаты касательной, проведенной к графику функции в данной точке, когда аргумент получает приращение .

28. Дифференцируемость функции, необходимые и достаточные условия дифференцируемости

Для того, чтобы функция f(x) была дифференцируема в точке x0 необходимо и достаточно, чтобы у нее существовала производная в этой точке. При этом Δy = f(x0+Δx)-f(x0) = f '(x0)Δx+α(Δx)Δx, где α(Δx) - бесконечно малая функция, при Δx→0. для функции одной переменной существование производной в точке является необходимым и достаточным условием дифференцируемости функции в этой точке. Для функции многих переменных дифференцируемость и существование частных производных не являются эквивалентными свойствами функции. Теорема 6 (необходимое условие дифференцируемости) . Если функция дифференцируема в точке, то она имеет в точке частные производные по каждой переменной и . При этом ,, где и – числа из равенства (1). Поэтому условие дифференцируемости (1) можно записать в виде а полный дифференциал функции – в виде Обратная теорема не верна, т. е. существование частных производных не является достаточным условием дифференцируемости функции.