Производная и ее применение

1. Понятие производной

Пусть дана функция y=f(x). Если выбрать некоторое значение аргумента х. то соответствующее ему значение функции называют начальным. Прибавим к начальному значению аргумента некоторое его приращение , получим х+ , тогда f(х+ ) будет наращенное значение функции. называется приращением функции.

y y=f(x)

f(х+ )

f(x)

x х+ x

Определение : Производной от функции f(x) называется предел отношения приращения функции к приращению аргумента при , т.е.

.

Нахождение производной функции называется дифференцированием. Операция дифференцирования обозначается штрихом, например: .

Геометрический смысл производной

Поясним геометрический смысл производной, рассмотрим рис 1. Из треугольника MM₁N получается, что угловой коэффициент секущей или тангенс угла её наклона к оси ОХ . Устремим теперь ∆х к нулю. При этом точка М₁ перемещается по кривой и приближается к точке М. В предельном положении хорда ММ₁ станет касательной МТ. Обозначим угол, образованный касательной с положительным направлением оси ОХ через φ.

Таким образом значение производной в некоторой точке равно угловому коэффициенту (тангенс угла наклона к оси ОХ) касательной в этой точке, проведенной к графику функции, т.е.

_{(рис 2)}

Найдем уравнение касательной к графику функции в точке М₀(х₀;y₀).

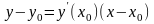- уравнение касательной к графику функции в точке х₀,

где у₀=у(х₀)

Рис 1

Рис 2

Физический смысл производной

Пусть s(t)-закон движения, v(t)- функция скорости, а(t)- функция ускорения. Тогда ,

т.е. производная от закона движения есть скорость.

Таблица производных

Для нахождения производных нет необходимости каждый раз применять определение, достаточно знать таблицу производных, например

. Эту производную мы получили по 3 пункту таблицы, приняв n=3.

2. Свойства производной

1. Производная суммы равна сумме производных

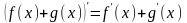
_Пример

_{Найти производную функции y = x2 − 5x.}

_{Решение}

2. Производная произведения равна сумме произведений производной одного множителя на другой

_Пример

_{Найти производную функции}

_{Решение}

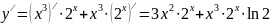
3. Постоянный коэффициент можно выносить за знак производной

_Пример

_{Найти производную функции 2√x − 3sin x}

_{Решение}

4. Производная частного равна дроби, числитель которой равен разности произведения производной числителя на знаменатель и произведения числителя на производную знаменателя, а знаменатель равен знаменателю в квадрате

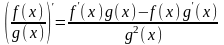
Пример

Найти производную функции

Решение