63) Производная. Геометрический и механический смысл.

Пусть функция f(x) определена на некотором промежутке X. Придадим значению аргумента в точке x₀ Х произволь­ное приращение Δx так, чтобы точка x₀ + Δx также принад­лежала X. Тогда соответствующее приращение функции f(x) составит Δу = f(x₀ + Δx) — f(x₀).

Определение 1. Производной функции f(x) в точке x₀ назы­вается предел отношения приращения функции в этой точке к приращению аргумента при Δx 0 (если этот предел сущест­вует).

Если в некоторой точке x₀ предел (4.1) бесконечен:

то говорят, что в точке x₀ функция f(x) имеет бесконечную производную.

Геометрический смысл производной. Определение 2. Касательной к графику функции у = f(x) в точке М называется предельное положение секущей MN, ког­да точка N стремится к точке М по кривой f(x).

Пусть точка М на кривой f(x) соответствует значению ар­гумента x₀, а точка N — значению аргумента x₀ + Δx (рис. 1). Из определения касательной следует, что для ее существования в точке x₀ необходимо, чтобы существовал предел 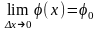, кот. равен углу наклона касательной к оси Оx. Из треугольника MNA следует:

Если производная функции f(x) в точке x₀ существует, то, согласно (1), получаем

Отсюда, что производная f'(x₀) равна угловому коэффициенту (тангенсу угла наклона к положительному направлению оси Ох) касательной к графику функции у = f(x) в точке М(x₀, f(x₀)). При этом угол наклона касательной определяется из формулы (2):

Физический смысл производной. Предположим, что функция l = f(t) описывает закон дви­жения материальной точки по прямой как зависимость пути l от времени t. Тогда разность Δl = f(t + Δt) - f(t) — это путь, пройденный за интервал времени Δt, а отношение Δl/Δt — средняя скорость за время Δt. Тогда предел 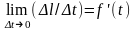определяет мгновенную скорость точки в момент вре­мени t как производную пути по времени.

64Дифференцируемость функции. Правило дифференцирования суммы, произведения, частного. Определение 1. Дифференциалом функции у = f(x) в точке x₀ называется главная линейная относительно Δx часть приращения функции в этой точке: Дифференциалом dx независимой переменной х будем называть приращение этой переменной Δx, т.е. соотношение (1) принимает вид Из равенства (2) производную f'(x) в любой точке х мож­но вычислить как отношение дифференциала функции dy к дифференциалу независимой переменной dx: Дифференциал функции имеет четкий геометрический смысл (рис. 1). Пусть точка М на графике функции у = f{x) соответствует значению аргумента x₀, точка N — зна­чению аргумента x₀ + Δx, MS — касательная к кривой f(x) в точке М, φ — угол между касательной и осью Ох. Тогда МА — приращение аргумента, AN — соответствующее при­ращение функции. Рассматривая треугольник АВМ, получа­ем, что АВ = Δx tg φ = f'(x₀) Δx = dy, т.е. это главная по по­рядку величины Δx и линейная относительно нее часть прира­щения функции Δу. Оставшаяся часть более высокого порядка малости соответствует отрезку BN.

9