
- •Правило треугольника
- •7) Основные сведения о матрицах
- •34)Угол между двумя плоскостями. Условие параллельности и перпендикулярности плоскостей.
- •48 Предел функции в точке.
- •49 Односторонние пределы
- •52) Второй замечательный предел.
- •53) . Бесконечно малые и бесконечно большие функции.
- •59) Первая теорема Больцано-Коши.
- •60 . Вторая теорема Больцано-Коши.
- •63) Производная. Геометрический и механический смысл.
34)Угол между двумя плоскостями. Условие параллельности и перпендикулярности плоскостей.
Уравнение поверхности
Уравнение линии
Отметим без
доказательства, что расстояние от точки
 до плоскости, заданной уравнением
до плоскости, заданной уравнением
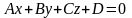 ,
находится по формуле
,
находится по формуле
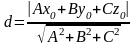 .
.
Поэтому координаты этих векторов пропорциональны, т.е.
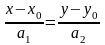
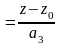 - (6.12)
- (6.12)
канонические уравнения прямой в пространстве, проходящей через точку .
Угол между двумя плоскостями
Найдем теперь угол
между плоскостями
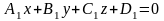 и
и
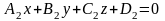 .
Поскольку векторы
.
Поскольку векторы
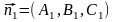 и
и
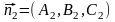 перпендикулярны данным плоскостям, то
угол
перпендикулярны данным плоскостям, то
угол
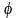 между ними равен двугранному углу между
плоскостями. Поэтому
между ними равен двугранному углу между
плоскостями. Поэтому
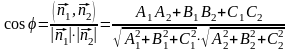 .
(6.8)
.
(6.8)
Если выражение в
(6.8) положительное, то
- острый угол, если отрицательное, то
оно соответствует тупому двугранному
углу
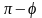 .
.
Условие параллельности и перпендикулярности двух плоскостей
Из формулы (6.8) получаем условие перпендикулярности двух плоскостей
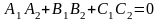 .
(6.9)
.
(6.9)
Условие параллельности двух плоскостей получается из условия коллинеарности векторов и :
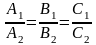 .
(6.10)
.
(6.10)
Если
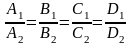 ,
то плоскости совпадают, так как их
уравнения отличаются постоянным
множителем.
,
то плоскости совпадают, так как их
уравнения отличаются постоянным
множителем.
35) Нормальное уравнение плоскости. Расстояние от точки до плоскости.
![]()
в векторной форме:
![]()
где
![]() -
единичный вектор,
-
единичный вектор,
![]() —
расстояние П. от начала координат.
Уравнение (2) может быть получено из
уравнения (1) умножением на нормирующий
множитель
—
расстояние П. от начала координат.
Уравнение (2) может быть получено из
уравнения (1) умножением на нормирующий
множитель
![]()
(знаки
![]() и
и
![]() противоположны).
противоположны).
Расстояние от точки до плоскости
Расстояние от точки до плоскости — это наименьшее из расстояний между этой точкой и точками плоскости. расстояние от точки до плоскости равно длине перпендикуляра, опущенного из этой точки на плоскость.
Расстояние
![]() от точки
от точки
![]() ,
до плоскости, заданной уравнением
,
до плоскости, заданной уравнением
![]() ,
вычисляется по формуле:
,
вычисляется по формуле:
![]()
36) Общее уравнение прямой. Каноническое уравнение прямой.
Общее уравнение прямой
Если
 не параллельна
не параллельна
 ,
то есть
,
то есть
 не коллинеарен
не коллинеарен
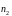 ,
то система уравнений
,
то система уравнений
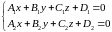 (3.42)
(3.42)
определяет прямую линию в пространстве.
|
Уравнения (3.42) называются общими уравнениями прямой в пространстве.
|
Каноническое уравнение прямой в пространстве
Отметим без доказательства, что расстояние от точки до плоскости, заданной уравнением , находится по формуле
.
Поэтому координаты этих векторов пропорциональны, т.е.
- (6.12)
канонические
уравнения прямой в пространстве,
проходящей через точку
.
Вектор
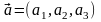 - направляющий вектор
прямой.
- направляющий вектор
прямой.
37) Параметрическое уравнение прямой
Обозначив общее
значение дробей в уравнении
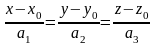 буквой
t,
т.е. положив
=
t,
получим
буквой
t,
т.е. положив
=
t,
получим
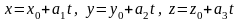 -
(6.13)
-
(6.13)
параметрические
уравнения прямой в пространстве,
проходящей через точку
в
направлении вектора
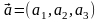 .
Параметр
.
Параметр
 .
.
38) Угол между прямыми в пространстве. Условие параллельности и перпендикулярности прямых в пространстве.
Углом между прямыми в пространстве называется угол между двумя пересекающимися прямыми, проходящими через произвольную точку пространства параллельно данным.
Из определения
следует, что
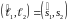 .
Если
.
Если
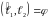 ,
то
,
то
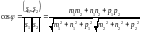 .
.
1)
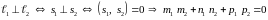 – условие перпендикулярности прямых.
– условие перпендикулярности прямых.
2)
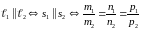 – условие параллельности прямых в
пространстве.
– условие параллельности прямых в
пространстве.
39) Расстояние от точки до прямой в пространстве. Условие параллельности и перпендикулярности прямых в пространстве.
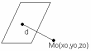
Расстояние от точки до прямой в пространстве
Пусть прямая задана уравнением Ax+By+Cz+D=0
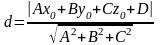
Условие параллельности и перпендикулярности прямых в пространстве.
Из формулы
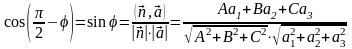 получаем условия параллельности
получаем условия параллельности
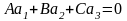
и перпендикулярности
прямой и плоскости
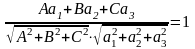
40) Угол между прямой и плоскостью
Пусть
- угол между прямой
и плоскостью
.
Тогда угол между векторами
(направляющий вектор прямой) и
(нормальный вектор плоскости) равен
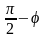 .
Поэтому
.
Поэтому
41)Числовая
последовательностьЕсли
каждому числу n
из ряда 1,2,3..n
поставлено в соответсвие вещественное
число xn,
то множество вещественных чисел
x1,x2…xn
наз-ся числовой последовательностью,
а xn -общим
членом последов-ти. Сокращено обоз-ся
{xn}.
Последовательность задана, если указано
условие получения любого ее элемента.
Пусть даны послед-ти {xn}
,{yn}.
Тогда суммой их называется последовательность
{xn+yn},
а разностью – {xn-yn}.
Произведением {xn}
на число m
назовем послед-ть {mxn}
Произведение {xn}
на {yn}
есть {xnyn},
а частное – {xn/yn},где
все члены {yn}
≠0. Последов-ть {xn}
называется ограниченной сверху (снизу),
если существует такое число M(m),
что любой элемент xn
этой последовательности удовлетворяет
неравенству xn≤M
(xn≥M).
Последовательность xn
наз-ся бесконечно большой, если для
любого A>0
существует такой номер N,
что при n>N
выполняется неравенство: |xn|>A.
Последовательность xn
наз-ся бесконечно малой, если для любого
ε>0 существует такой номер N,
что при n>N
выполняется неравенство: |xn|<
ε. Если xn-бесконечно
большая посл-ть и все ее члены отличны
от нуля, то послед-ть {1/xn}
является бесконечно малой.
Число а
называется пределом
последовательности {xn},
если для любого положительного числа
ε
существует такой номер N,
что при всех п
> N выполняется
неравенство![]()
44)Сходимость последовательностей в пространстве Rn
Последовательность, имеющая предел, называется сходящейся. Если последовательность имеет своим пределом число а, то это записывается так: Последовательность, не имеющая предела, называется расходящейся
.45 Открытые и замкнутые множества в Rn. Предельные точки множества. Множество точек пространства Rn называется открытым, если вместе с каждой своей точкой оно содержит некоторую окрестность этой точки. Множество называется замкнутым, если оно включает все свои граничные (предельные) точки, т.е. точки, окрестности которых содержат точки как принадлежащие множеству, так и не принадлежащие ему. Пусть Х - множество в пространстве Rn. Точка р называется внутренней точкой множества Х, если существует шар В (р; r) ( р- центр, r-радиус), все точки которого принадлежат множеству Х. Точка р называется внешней точкой по отношению к Х, если существует шар В (р;r) ,ни одна точка которого не принадлежит множеству Х. Точка р называется граничной, если она не является ни внутренней, ни внешней. Множество Х называется открытым, если каждая его точка является внутренней. Пусть Х-множество в пространстве Rn. Точка р0 называется предельной для множества Х, если в любой окрестности точки р0 имеются точки множества Х, отличные от р0. При этом точка р0 может как принадлежать, так и не принадлежать множеству Х. Точка р0 называется изолированной точкой, если существует такой шар В (р0;ε), в котором никаких точек из Х, кроме точки р0 не имеется
46. Число е. Задача на вычисление сложных процентов.
Рассмотрим
последовательность {хп},
общий член которой выражается формулой
![]() В
курсе математического анализа
доказывается, что эта последовательность
монотонно
возрастает
и имеет предел. Этот предел называют
числом е.
Следовательно, по определению
В
курсе математического анализа
доказывается, что эта последовательность
монотонно
возрастает
и имеет предел. Этот предел называют
числом е.
Следовательно, по определению
![]() Число
е
играет большую роль в математике..
Отметим , что число е
является иррациональным; его приближенное
значение равно е
= 2,7182818...
Число
е
играет большую роль в математике..
Отметим , что число е
является иррациональным; его приближенное
значение равно е
= 2,7182818...
47.Понятие функции
Пусть Х
и Y
— некоторые числовые множества и
пусть каждому элементу x
![]() Х
по какому-либо закону f
поставлен в соответствие один элемент
у
Y.
Тогда говорят, что определена
функциональная
зависимость
у
от x
по закону у
= f(x).
При этом x
называют независимой
переменной (или аргументом), у —
зависимой переменной,
множество Х
— областью определения
(существования) функции, множество
Y
— областью
значений
(изменения) функции.
Существуют три основных способа
задания функций: табличный,
аналитический и графический
.1.
Табличный способ широко используется
в приложениях. В таких таблицах одну
из переменных можно принять за
независимое, тогда другие причины будут
функциями от этого аргумента.
2. Аналитический способ. Этот способ
состоит в задании связи между
аргументом и функцией в виде формул.
3. Графический способ. Здесь
соответствие между аргументом и
функцией задается посредством графика.
Область
определения функции
1. Когда
функция задана в аналитическом виде
y
= f
(x)
область ее определения
такова: подкоренное выражение в корне
четной степени не может быть отрицательным,
знаменатель дроби = 0, выражение под
знаком логарифма должно быть только
положительным и др.
2. Область
определения функции бывает задана
вместе с функцией f(x).
Например, 1 ≤ х ≤ 4.
Функция у = f(x)
называется четной, если для любых
значений аргумента из области ее
определения выполнено равенство
f(-x)=f(x)
Функция у = f(x)
называется нечетной, если:
f(-x)=-f(x)
Х
по какому-либо закону f
поставлен в соответствие один элемент
у
Y.
Тогда говорят, что определена
функциональная
зависимость
у
от x
по закону у
= f(x).
При этом x
называют независимой
переменной (или аргументом), у —
зависимой переменной,
множество Х
— областью определения
(существования) функции, множество
Y
— областью
значений
(изменения) функции.
Существуют три основных способа
задания функций: табличный,
аналитический и графический
.1.
Табличный способ широко используется
в приложениях. В таких таблицах одну
из переменных можно принять за
независимое, тогда другие причины будут
функциями от этого аргумента.
2. Аналитический способ. Этот способ
состоит в задании связи между
аргументом и функцией в виде формул.
3. Графический способ. Здесь
соответствие между аргументом и
функцией задается посредством графика.
Область
определения функции
1. Когда
функция задана в аналитическом виде
y
= f
(x)
область ее определения
такова: подкоренное выражение в корне
четной степени не может быть отрицательным,
знаменатель дроби = 0, выражение под
знаком логарифма должно быть только
положительным и др.
2. Область
определения функции бывает задана
вместе с функцией f(x).
Например, 1 ≤ х ≤ 4.
Функция у = f(x)
называется четной, если для любых
значений аргумента из области ее
определения выполнено равенство
f(-x)=f(x)
Функция у = f(x)
называется нечетной, если:
f(-x)=-f(x)
