
- •Правило треугольника
- •7) Основные сведения о матрицах
- •34)Угол между двумя плоскостями. Условие параллельности и перпендикулярности плоскостей.
- •48 Предел функции в точке.
- •49 Односторонние пределы
- •52) Второй замечательный предел.
- •53) . Бесконечно малые и бесконечно большие функции.
- •59) Первая теорема Больцано-Коши.
- •60 . Вторая теорема Больцано-Коши.
- •63) Производная. Геометрический и механический смысл.
/1)Векторы в пространстве:
Вектор – направленный отрезок называется вектором ā
Вектором наз. упорядоченная совокупность чисел Х={X1,X2,...Xn} вектор дан в n-мерном пространстве. Т(X1,X2,X3). n=1,2,3. Геометрический вектор - направленный отрезок. |AB|=|a| - длинна. 2 вектора наз. коллинеарными, если они лежат на 1 прямой или ||-ных прямых. Векторы наз. компланарными, если они лежат в 1-ой плоскости или в ||-ных плоскостях. 2 вектора равны, когда они коллинеарны, сонаправленны, и имеют одинак-ую длинну.
Линейные операции над векторами обладают следующими свойствами:
1. а+b=b+а
2. (а +b) +с=а + (b +с),
3. λ1 • (λ2 •а) =λ1 •λ2 •а,
4. (λ1 +λ2) •а =λ1 •а +λ2 •а,
5. λ • (а +b) =λ •а+λ •b.
Операции с векторами:
Сложение (результат - вектор)
Правило треугольника
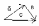
Правило параллелограмма
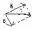
Если вектора заданы в прямоугольной системе координат ā (а1,а2), в-(в1,в2), то чтобы найти сумму надо сложить с-(а1+в1;а2+в2)
2) Арифметические векторы пространства R
Арифметическим вектором называется упорядоченная совокупность n чисел.
Обозначается x = (x1, x2, ..., xn);
числа x1, x2, ..., xn называются компонентами арифметического вектора.
Для арифметических векторов определены линейные операции — сложениеарифметических векторов и умножение вектора на число:
для любых x = (x1, x2, ..., xn), y = (y1, y2, ..., yn) и любого числа α справедливо:
x + y = (x1+ y1, x2 +y2, ..., xn+ yn); αx = (αx1, αx2, ..., αxn).
Множество арифметических векторов, для которых определены операции сложения и умножения на число называется пространством арифметических векторов Rn.
Вектор θ = (0, 0, ..., 0) называется нулевым вектором Rn,
а вектор −x = (−x1, −x2, ..., −xn) — противоположным вектором для вектора x вRn.
3)Скалярное произведение двух векторов в пространстве определяется аналогично случаю на плоскости:
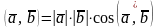 .
.
Формула скалярного квадрата:
 .
.
Справедлива формула, связывающая скалярное произведение векторов и проекции этих векторов:
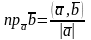 .
(1)
.
(1)
4)Линейная зависимость векторов. Действия над векторами в координатной форме
Векторы
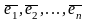 называются линейно
независимыми,
если равенство
называются линейно
независимыми,
если равенство
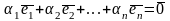
справедливо тогда
и только тогда, когда
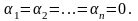 В противном случае эти векторы называются
линейно
зависимыми.
Для того чтобы векторы
были линейно зависимыми, необходимо и
достаточно, чтобы хотя бы один из них
можно было представить в виде линейной
комбинации остальных.
В противном случае эти векторы называются
линейно
зависимыми.
Для того чтобы векторы
были линейно зависимыми, необходимо и
достаточно, чтобы хотя бы один из них
можно было представить в виде линейной
комбинации остальных.
5) Ортогональность векторов
Ортогональными (перпендикулярными) называются векторы, скалярное произведение которых равно нулю. Это определение применимо к любым пространствам с положительно определённым скалярным произведением. Важной особенностью понятия является его привязка к конкретному используемому скалярному произведению: при смене произведения ортогональные элементы могут стать неортогональными, и наоборот.
6)Базис пространства R
Базис векторного пространства и его размерности.
Базисом на плоскости называется совокупность фиксированной точки и 2х неколлинеарных векторов, проведенных к ней.
Базисом в пространстве наз. совокупность фиксированной точки в пространстве и 3х некомпланарных векторов.
Любой вектор на плоскости может быть разложен по векторам базиса на плоскости. Любой вектор в пространстве может быть разложен по векторам базиса в пространстве.
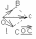
ОС=OA+OB, OA=x*i, OB=j*y, OC=xi+yj. Числа х,у называются координатами вектора ОС в данном базисе

(НЕОБЯЗАТЕЛЬНО)Упорядоченная
тройка
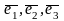 ненулевых линейно-независимых векторов
образует базис
в трехмерном пространстве. Любой вектор
ненулевых линейно-независимых векторов
образует базис
в трехмерном пространстве. Любой вектор
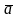 пространства единственным образом
может быть разложен
по базисным векторам,
т.е. представлен в виде
пространства единственным образом
может быть разложен
по базисным векторам,
т.е. представлен в виде
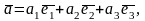
где
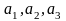 – координаты вектора
в базисе
(записывают:
– координаты вектора
в базисе
(записывают:
 ).
).
В пространстве линейная независимость векторов равносильна их некомпланарности, т.е. любые три некомпланарных вектора, взятые в определенном порядке, образуют базис.
Пусть задана тройка
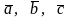 некомпланарных векторов. Совместим
начала этих векторов. Если кратчайший
поворот вектора
до направления вектора
некомпланарных векторов. Совместим
начала этих векторов. Если кратчайший
поворот вектора
до направления вектора
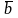 ,
наблюдаемый с конца вектора
,
наблюдаемый с конца вектора
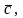 совершается против часовой стрелки,
то тройка векторов
называется правой.
В противном случае – левой.
Всюду далее рассматриваются правые
тройки базисных векторов.
совершается против часовой стрелки,
то тройка векторов
называется правой.
В противном случае – левой.
Всюду далее рассматриваются правые
тройки базисных векторов.
В случае, когда
базисные векторы попарно перпендикулярны,
система координат называется прямоугольной
декартовой.
Если добавить, кроме того, условие
нормированности базисных векторов
(т.е. их единичную длину), то такой базис
называют ортонормированным
и обозначают
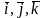 :
:
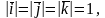
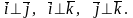 Прямоугольные декартовы координаты
вектора
является его проекциями на вектора
соответственно.
Прямоугольные декартовы координаты
вектора
является его проекциями на вектора
соответственно.
Если точка M имеет прямоугольные декартовы координаты x, y, z в системе координат с началом в точке O(0, 0, 0) и базисом , то соответствующий радиус-вектор
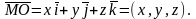
Если
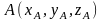 и
и
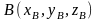 ,
то
,
то
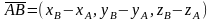 .
.
Линейные
операции для векторов
 и
и
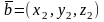 в координатной форме и их скалярное
произведение вычисляются по формулам:
в координатной форме и их скалярное
произведение вычисляются по формулам:
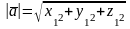 ;
(4)
;
(4)
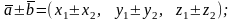 (5)
(5)
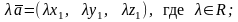 (6)
(6)
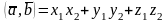 ;
(7)
;
(7)
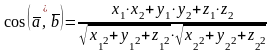 .
(8)
.
(8)
Направляющими
косинусами
вектора
называются величины
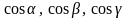 ,
где
,
где
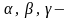 углы,
которые образует вектор
соответственно с осями
углы,
которые образует вектор
соответственно с осями
 .
Их вычисляют по формулам:
.
Их вычисляют по формулам:
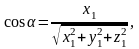
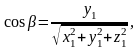 (9)
(9)

Если
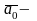 единичный
вектор, то
единичный
вектор, то
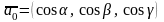 .
.
