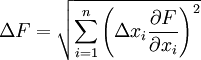1. Прямые, косвенные, совокупные измерения. Методы измерений.

В общем случае измерением называется процесс нахождения опытным путем с помощью специальных технических средств соотношения между измеряемой величиной и некоторым ее значением, принятым за единицу сравнения.

Прямыми называют такие измерения, при которых значение измеряемой величины определяют непосредственно из опытных данных. Прямые измерения производят следующими основными методами: непосредственной оценки, дифференциаль­ным, противопоставления, нулевым.

Методом непосредственной оценки измеряемая величина пре­образуется в выходную величину прибора, т. е. приборы не­посредственно показывают (или записывают) измеряемую вели­чину. Метод непосредственной оценки широко используют в при­борах промышленного контроля.

При дифференциальном (разностном) методе прибор непосред­ственно определяет разность между измеряемой и некоторой известной величиной (мерой), после чего измеряемую величину находят алгебраическим сложением.

Метод противопоставления — это метод сравнения с мерой, при котором измеряемая величина и величина, воспроизводимая мерой, одновременно воздействуют на прибор сравнения, с по­мощью которого устанавливают соотношение между этими ве­личинами. Например, на рычажных весах массу взвешиваемого груза находят по массе установленных гирь.

Нулевой (компенсационный) метод — это метод сравнения мерой, при котором результирующий эффект воздействия ве­личин на прибор сравнения доводят до нуля. К приборам, основанным на компенсационном методе, относятся потенциометры, уравновешенные мосты и др.

Косвенными называют такие измерения, при которых измеряе­мую величину определяют на основании известной зависимости между этой величиной и величинами, подвергаемыми прямым измерениям. Косвенные измерения широко применяют при контроле произ­водственных процессов, когда прямые измерения невозможны.

При совокупных измерениях числовые значения измеряемой величины определяют решением системы уравнений, полученных из совокупности прямых измерений одной или нескольких одноименных величин (например, определение температурного коэф­фициента линейного расширения).

2.Погрешности измерительных приборовПогрешностью измерения называют отклонение результата измерения от истинного значения измеряемой величины. За по­грешность измерения не следует принимать погрешность измери­тельного прибора, с помощью которого производится измерение. Погрешностью измерительного прибора является разность между показанием прибора и истинным значением измеряемой величины. Погрешность измерения обусловлена многими характеристиками измерительного процесса, в том числе и погрешностью измери­тельного прибора. Погрешность измерительного прибора определяется структур­ными и конструктивными особенностями самого прибора, свой­ствами примененных в нем материалов и элементов, особенно­стями технологии изготовления, градуировки. Погрешности приборов можно классифицировать по различ­ным признакам: единице измерения величины; характеру связи между величиной погрешности и измеряемой величиной; законо­мерности появления погрешности при многократных испытаниях прибора; условиям и причинам появления погрешности. В зависимости от единицы измерения различают абсолютные, относительные и приведенные погрешности.

Абсолютная погрешность, средства измерения (СИ) выражается в единицах измеряемой величины х или выходного сигнала у измерительного преобразователя (ИП). Абсолютная погрешность СИ в единицах х (или погрешность, приведенная ко входу СИ) равна разности между показанием прибора х_и и истинным значе­нием измеряемой величины Относительная погрешность СИ равна отношению абсолют­ной погрешности х или А_у к действительному значению х₀ измеряе­мой величины х или выходного сигнала ИП у₀:

Приведенная погрешность — отношение абсолютной погреш­ности СИ к нормирующему значению . Чаще сего нормирующее значение выбирают равным величине диапа­зона измерений: X_N = X_max — X_mln. Величины обычно выражают процентах.

3.Метрологические характеристикиКласс точности — основная метрологическая характеристика прибора, определяющая допустимые по стандарту значения основных и дополнительных погрешностей, влияющих на точность измерения.Погрешность может нормироваться, в частности, по отношению к:результату измерения (по относительной погрешности)в этом случае, по ГОСТ 8.401-80 (взамен ГОСТ 13600-68), цифровое обозначение класса точности (в процентах) заключается в кружок.длине (верхнему пределу) шкалы прибора.Чувствительность измерительного прибора - отношение изменения сигнала на выходе измерительного прибора к вызывающему его изменению измеряемой величины. Основная погрешность – это погрешность, полученная в нормальных условиях эксплуатации средства измерений (при нормальных значениях влияющих величин).Измерительным приборам, пределы допускаемой основной погрешности которых заданы в виде приведённых основных (относительных) погрешностей, присваивают классы точности, выбираемые из ряда следующих чисел: (1; 1,5; 2,0; 2,5; 3,0; 4,0; 5,0; 6,0)*10ⁿ, где показатель степени n = 1; 0; −1; −2 и т. дВариация показаний измерительного прибора - разность показаний прибора в одной и той же точке диапазона измерений при плавном подходе "справа" и подходе "слева" к этой точке. Порог чувствительности средства измерений - наименьшее изменение измеряемой величины, вызывающее заметное изменение выходного сигнала средства измерений.

4. Случайная погрешность — погрешность, меняющаяся (по величине и по знаку) от измерения к измерению. Случайные погрешности могут быть связаны с несовершенством приборов (трение в механических приборах и т. п.), тряской в городских условиях, с несовершенством объекта измерений (например, при измерении диаметра тонкой проволоки, которая может иметь не совсем круглое сечение в результате несовершенства процесса изготовления), с особенностями самой измеряемой величины (например при измерении количества элементарных частиц, проходящих в минуту через счётчик Гейгера).Систематическая погрешность — погрешность, изменяющаяся во времени по определённому закону (частным случаем является постоянная погрешность, не изменяющаяся с течением времени). Систематические погрешности могут быть связаны с ошибками приборов (неправильная шкала, калибровка и т. п.), неучтёнными экспериментатором.Грубая погрешность (промах) — погрешность, возникшая вследствие недосмотра экспериментатора или неисправности аппаратуры (например, если экспериментатор неправильно прочёл номер деления на шкале прибора или если произошло замыкание в электрической цепи).Диспе́рсия све́та (разложение света) — это явление зависимости абсолютного показателя преломления вещества от длины волны (или частоты) света (частотная дисперсия), или, что то же самое, зависимость фазовой скорости света в веществе от длины волны (или частоты). Экспериментально открыта Ньютоном около 1672 года, хотя теоретически достаточно хорошо объяснена значительно позднее. Математи́ческое ожида́ние — мера среднего значения случайной величины в теории вероятностей.

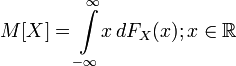
5. Доверительный интервал, Доверительная вероятность, Нормальное распределение, Распределение Стьюдента, Погрешность косвенных воспроизводимых измерений .

Доверительный интервал в математической статистике — это интервал, построенный с помощью случайной выборки из распределения с неизвестным параметром, такой, что он накрывает данный параметр с заданной вероятностью.

Доверительная вероятность — вероятность того, что значение параметра генеральной совокупности находится в построенном для него доверительном интервале. Доверительная вероятность обычно обозначается (1 — α) и выбирается из значений 0,9; 0,95; 0,99 и т. п.

Нормальное распределение, также называемое гауссовским распределением или распределением Гаусса — распределение вероятностей, которое задается функцией плотности распределения:

где параметр μ — среднее значение (математическое ожидание) случайной величины и указывает координату максимума кривой плотности распределения, а σ² — дисперсия.

Нормальное распределение зависит от двух параметров — смещения и масштаба, то есть является с математической точки зрения не одним распределением, а целым их семейством. Значения параметров соответствуют значениям среднего (математического ожидания) и разброса (стандартного отклонения).

Распределение Стьюдента в теории вероятностей — это однопараметрическое семейство абсолютно непрерывных распределений.

Пусть — независимые стандартные нормальные случайные величины, такие что . Тогда распределение случайной величины , где

называется распределением Стьюдента с степенями свободы. Пишут . Её распределение абсолютно непрерывно и имеет плотность

,

где — гамма-функция Эйлера.

Погрешность косвенных воспроизводимых измерений — погрешность вычисляемой (не измеряемой непосредственно) величины:

Если F = F(x₁,x₂...x_n), где x_i — непосредственно измеряемые независимые величины, имеющие погрешность Δx_i, тогда: