
- •Введение
- •1. Основные понятия теории вероятностей Операции над событиями
- •Частость наступления события
- •Свойства частости
- •Аксиоматика теории вероятности Построение вероятностного пространства
- •Теорема о продолжении меры
- •Определение вероятностного пространства
- •Классическое определение вероятности
- •Условная вероятность
- •Обоснование формулы условной вероятности в общем случае
- •Независимые события
- •Формула сложения вероятностей
- •Формула полной вероятности
- •Формула Байеса
- •Композиция испытаний
- •Композиция n испытаний
- •Композиция n независимых испытаний
- •Биномиальное распределение
- •Случайная величина Теорема Колмогорова
- •Дискретные случайные величины
- •Вероятностные характеристики дискретных случайных величин
- •Свойства математического ожидания
- •Производная функция
- •Первая модель распределения Пуассона
- •Вторая модель распределения Пуассона
- •Непрерывные случайные величины
- •Свойства плотности вероятности
- •Второе эквивалентное определение плотности вероятности
- •Вероятностные характеристики непрерывных случайных величин
- •Распределение Гаусса - нормальное
- •Функция Лапласа
- •Неравенство Чебышева
- •Многомерные случайные величины
- •Аксиоматика. Формальная вероятностная модель
- •Двумерные случайные величины
- •Двумерные непрерывные случайные величины
- •2. Основы математической статистики
- •2.1. Основные понятия математической статистики
- •Интервальная группировка и представление выборочных данных
- •Числовые характеристики распределения выборки
- •Точечные статистические оценки параметров распределения
- •2.1.5.3. "Исправленная" дисперсия и "исправленное" среднее квадратическое отклонение
- •Интервальные статистические оценки параметров распределения (доверительные интервалы)
- •2.1.6.3. Доверительный интервал для математического ожидания нормального распределения случайной величины
- •Основные законы распределения, используемые в статистических исследованиях
- •Асимметрия и эксцесс распределения
- •2.2. Основные методы математической статистики
- •2.2.1. Проверка статистических гипотез
- •Проверка гипотезы о нормальном распределении генеральной совокупности. Критерий Колмогорова
- •2.2.2. Исследование статистических различий между двумя выборками
- •Список использованных источников
- •Содержание Справочные материалы
- •Значения функции
- •Значения нормально распределенной случайной величины z
- •На интервале [0,1]
- •Значения функции
- •Табличные (критические) значения функции распределения χ2
Теорема о продолжении меры
Построим минимальную - алгебру, которой принадлежит поле событий F (например, борелевская - алгебра - это минимальная - алгебра, которая содержит поле всех полуинтервалов ненулевой длины).
Тогда доказывается, что счетно-аддитивная функция P(A) однозначно распространяется на все элементы минимальной - алгебры и при этом ни одна из аксиом не нарушается.
Таким образом, продленное P(A) называется - аддитивной мерой.
- алгебра содержит ненаблюдаемые события наряду с наблюдаемыми.
Но в аксиоматической теории вероятности считается, что может произойти любое событие из - алгебры.
Расширение поля наблюдаемых событий на - алгебру связано с невозможностью получить основные результаты теории вероятности без понятия - алгебры.
Определение вероятностного пространства
Вероятностным пространством называется тройка (, , P), где
- пространство элементарных событий, построенное для данного испытания;
- -алгебра, заданная на - системе возможных событий, которая интересует исследователя, в результате проводимых испытаний;
P - - аддитивная мера, т.е. - аддитивная неотрицательная функция, аргументами которой являются аргументы из - алгебры и удовлетворяющая трем аксиомам теории вероятности.
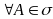
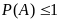 .
P(A) - называется вероятностью наступления
события A.
.
P(A) - называется вероятностью наступления
события A.Вероятность достоверного события равна 1 P()=1.
Вероятность суммы несовместных событий равна сумме вероятностей
![]()
,
![]() .
.
k - возможно бесконечное число.
Следствие:
Вероятность невозможного события равна 0.
По определению суммы имеет место неравенство +V=. и V несовместные события.
По третей аксиоме теории вероятности имеем:
P(+V)=P(Q)=P(U)=1
P()+P(V)=P()
1+P(V)=1
P(V)=1
Пусть
состоит из конечного числа элементарных
событий ={E1,
E2,...,
Em}
тогда по определению
![]() .
Элементарные события несовместны, тогда
по третей аксиоме теории вероятности
имеет место
.
Элементарные события несовместны, тогда
по третей аксиоме теории вероятности
имеет место
![]()
Пусть некоторое
событие A
состоит из k элементарных событий, тогда
{Ei1,
Ei2,...,
Eik}
![]()
Доказать: Если AB, то P(B)P(A), B=A+C, A и C несовместны.
* Пусть B=A+C, A и B несовместны. Тогда по третей аксиоме теории вероятности P(B)=P(A+C)=P(A)+P(C) т.к. 1P(C)0 - положительное число, то P(B)P(A).
Классическое определение вероятности
Пусть состоит из конечного числа элементарных событий и все элементарные события равновероятны, т.е. ни одному из них из них нельзя отдать предпочтения до испытания, следовательно, их можно считать равновероятными.
Тогда достоверное
событие
![]() m - количество равновероятных событий
m - количество равновероятных событий
![]() ,
,
![]() ,
,
![]()
Пусть произвольное
событие
![]() Тогда
Тогда
![]() ,
т.е. событие A состоит из k элементарных
событий.
,
т.е. событие A состоит из k элементарных
событий.
Если элементарные события являются равноправными, а, следовательно, и равновероятными, то вероятность наступления произвольного события равна дроби числитель которой равен числу элементарных событий, входящих в данное, а знаменатель - общее число элементарных событий.
Условная вероятность
P(A/B)
Условной вероятностью наступления события A, при условии события B, называется вероятность наступления события A в результате испытаний, если известно, что в это испытании произошло событие B.
Вывод формулы условной вероятности для случая равновероятных элементарных событий

Действительно, в данном испытании произошло одно из t событий, входящих в B. Все элементарные события равновероятны, следовательно, для данного испытания вероятность наступления произвольного элементарного события, входящего в B равна 1/t. Тогда по классическому определению вероятности, в данном испытании событие A произойдет с вероятностью r/t.
![]()
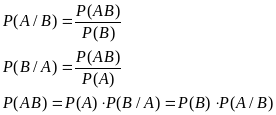
В общем случае доказать эту формулировку невозможно, в теории вероятности она вводится как правило. Существует лишь толкование этой формулы.
