Асимметрия и эксцесс распределения

Предварительно отметим, что асимметрия и эксцесс – это числовые характеристики, выражающие количественную меру степени близости данного распределения к нормальному.

Коэффициенты асимметрии и эксцесса теоретического распределения

Под теоретическим распределением понимается распределение вероятностей изучаемого признака Х генеральной совокупности, который трактуется как случайная величина Х. Для случайной величины Х введем безразмерные числовые характеристики:

, ,

которые называются соответственно коэффициентами асимметрии и эксцесса теоретического распределения. Они оценивают степень близости данного распределения к нормальному, а также характеризуют форму закона распределения вероятностей изучаемой случайной величины Х.

П режде всего отметим, что для нормального распределения коэффициенты асимметрии и эксцесса равны нулю: , .

Рис. 12. Кривые распределения:

а – ; б –

Если для данного распределения , то длинная часть кривой распределения (графика плотности ) расположена справа от вершины (рис.12,а); если же , то длинная часть кривой распределения расположена слева от вершины (рис.12,б).

Если для данного распределения , то кривая распределения имеет более высокую и острую вершину, чем нормальная кривая Гаусса (рис.13,а); если же , то кривая распределения имеет более низкую и пологую вершину, чем нормальная кривая (рис. 13,б). При этом сравнении предполагается, что данное и нормальное распределения имеют одинаковые математические ожидания и дисперсии.

С равнительно небольшие по модулю значения коэффициентов и свидетельствуют о близости данного распределения к нормальному. Большие же значения и указывают на значительное отклонение данного распределения от нормального.

Рис. 13. Кривая распределения:

а – ; б –

Выборочные коэффициенты асимметрии и эксцесса

Приведенные ниже коэффициенты являются точечными статистическими оценками коэффициентов асимметрии и эксцесса теоретического распределения, вычисленными по выборке, представленной в виде интервального статистического ряда.

,

.

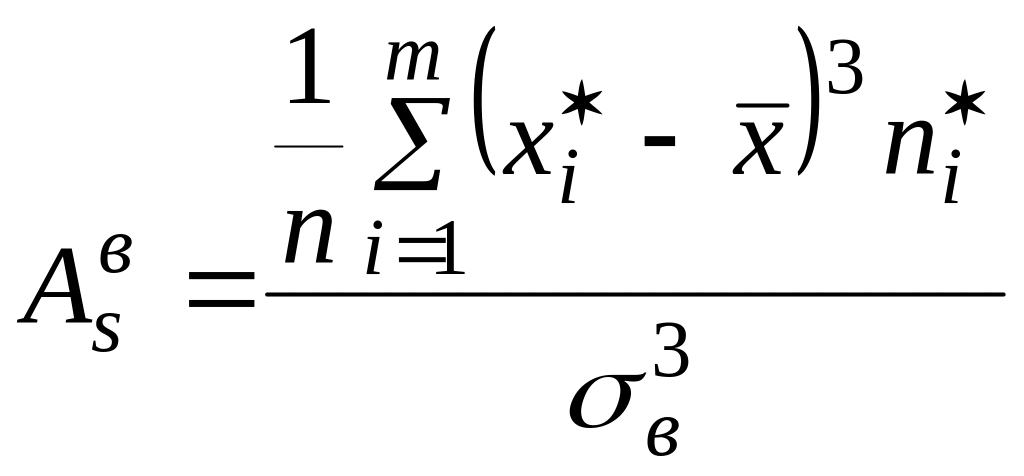Выборочные коэффициенты асимметрии и эксцесса можно использовать для упрощенной проверки гипотезы о нормальности распределения. При этом необходимо руководствоваться следующими правилами:

1. Если оба выборочных коэффициента асимметрии и эксцесса по модулю меньше соответствующих табличных критических значений

и ,

то распределение изучаемой генеральной совокупности достаточно близко к нормальному.

2. Если хотя бы один из модулей коэффициентов или окажется больше соответствующего табличного критического значения

или ,

то распределение изучаемой генеральной совокупности существенно отличается от нормального.

Таблица критических значений коэффициентов асимметрии и эксцесса приведена в учебном пособии В.И. Лупандина "Математические методы в психологии".

С целью существенного упрощения вычислений коэффициентов , применим метод условных вариант. В интервальном статистическом ряде перейдем к условным вариантам ( ). В условных вариантах формулы для и запишутся следующим образом:

,

,

где , , , , , .

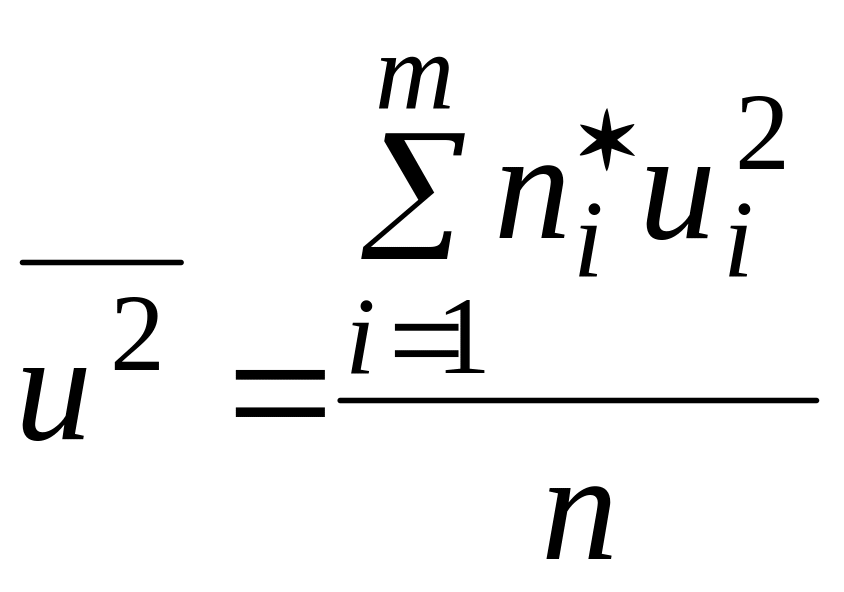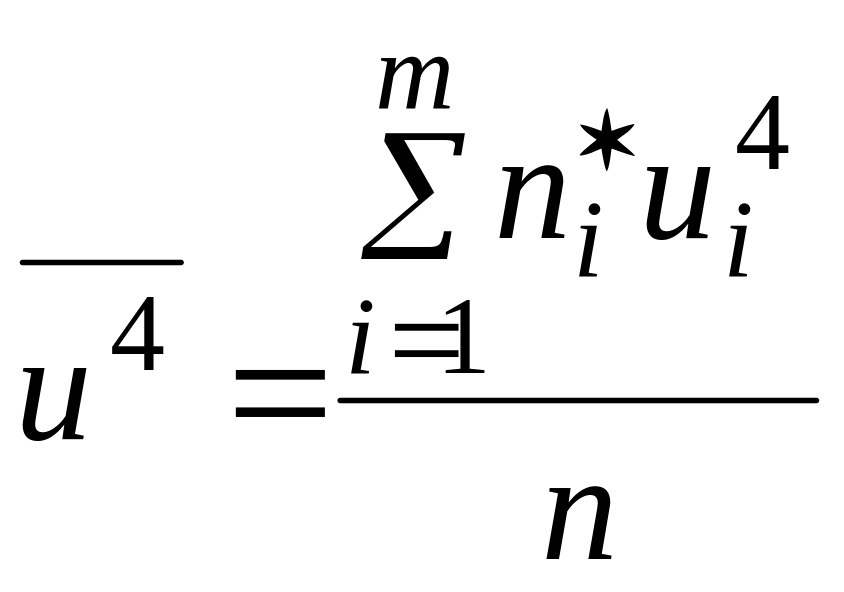Для удобства вычисления организуются в форме расчетной таблицы (см. пример).

Пример. Дан интервальный статистический ряд

	50–53	53–56	56–59	59–62	62–65	65–68
	1	2	11	21	11	4

Найти выборочные коэффициенты асимметрии и эксцесса , .

Составим расчетную таблицу следующей формы:

1	50–53	51,5	1	–3	–3	9	9	–27	–27	81	81
2	53–56	54,5	2	–2	–4	4	8	–8	–16	16	32
3	56–59	57,5	11	–1	–11	1	11	–1	–11	1	11
4	59–62	60,5	21	0	0	0	0	0	0	0	0
5	62–65	63,5	11	1	11	1	11	1	11	1	11
6	65–68	66,5	4	2	8	4	16	8	32	16	64
	–	–	50	–	1	–	55	–	–11	–	199
	–	–	–	–	0,02	–	1,1	–	–0,22	–	3,98

Здесь , , ; , .

Далее последовательно находим:

; ;

;

.

Таким образом, =–0,248, =0,309.