Содержание

стр.

Введение	3
1 Общие сведения о построении комбинационных и последовательностных схем	4
2 Триггеры 2.1 Общие сведения о триггерах 2.2 Классификация триггеров 2.3 RS-триггер	9 9 10 13
3 Синтез логической функции для синхронного RS - триггера	18
4 Разработка логической схемы синхронного RS - триггера	19
5 Построение электрической принципиальной схемы синхронного RS – триггера	20
Заключение	21
Приложения	22

Введение

Логические элементы — устройства, предназначенные для обработки информации в цифровой форме (последовательности сигналов высокого — «1» и низкого — «0» уровней в двоичной логике, последовательность «0», «1» и «2» в троичной логике, последовательности «0», «1», «2», «3», «4», «5», «6», «7», «8» и «9» в десятичной логике).

Логические элементы подразделяются по типу использованных в них электронных элементов. Наибольшее применение в настоящее время находят следующие логические элементы:

• РТЛ (резисторно-транзисторная логика);

• ДТЛ (диодно-транзисторная логика);

• ТТЛ (транзисторно-транзисторная логика).

Комбинационными называются такие логические устройства, выходные сигналы которых однозначно определяются входными сигналами (шифратор, дешифратор, мультиплексор, демультиплексор, полусумматор и сумматор), все они выполняют простейшие двоичные, троичные или n-ичные логические функции.

Последовательностными называют такие логические устройства, выходные сигналы которых определяются не только сигналами на входах, но и предысторией их работы, то есть состоянием элементов памяти. Основные последовательностные устройства это:

• Триггер;

• Счётчик импульсов;

• Регистр.

В данной курсовой работе будет рассмотрена реализация RS-триггера на базе микросхемы К155ЛА.

1 Общие сведения о построении комбинационных и последовательностных схем

Для реализации функций алгебры логики используются логические элементы, на основе которых создаются логические схемы. Элементы в схемах могут быть однотипные или разнотипные. Логические схемы могут иметь n входов и один или m выходов. Выходные функции задаются набором (комбинацией) входных сигналов и поэтому называются комбинационными схемами (КС).

Синтез комбинационных схем включает в себя следующие этапы:

- постановка задачи;

- составление таблицы истинности, в которой отражена заданная функция при соответствующих сочетаниях переменных;

- построение схемы с учетом оптимального набора элементов.

Одна из основных задач синтеза заключается в выборе типов элементов, на которых будут реализовываться заданные функции. Поэтому необходимо определить минимальный набор логических элементов (базис), образующих функционально полную систему элементов.

Базис – это функционально полный набор элементов, с помощью которого можно реализовать сколь угодно сложную переключательную функцию. Их может быть несколько. Базис из логических элементов И, ИЛИ, НЕ называется основным.

Элемент «И» (AND), иначе его называют «конъюнктор».

В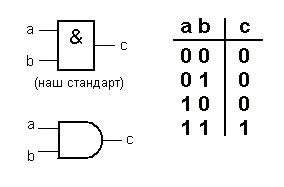 от так выглядит элемент «И» и его таблица истинности:

Рисунок 1.1 – Элемент «И»

Единица на выходе элемента «И» возникает только тогда, когда на оба входа поданы единицы. Это объясняет название элемента: единицы должны быть И на одном, И на другом входе.

Таблица 1.1 – Таблица истинности элемента «И»

Входы		Выход
a	b	a И b
0	0	0
0	1	0
1	0	0
1	1	1

Элемент «ИЛИ» (OR),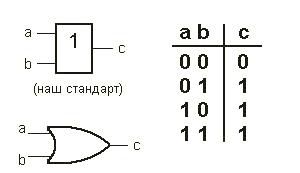 иначе его называют «дизъюнктор».

Рисунок 1.2 – Элемент ИЛИ

На выходе возникает единица, когда на один ИЛИ на другой ИЛИ на оба сразу входа подана единица.

Таблица 1.2 – Таблица истинности элемента «ИЛИ»

Входы		Выход
a	b		a ИЛИ b
0	0		0
0	1		1
1	0		1
1	1		1

Элемент «НЕ» (NOT),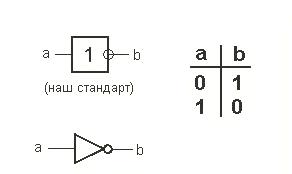 чаще его называют «инвертор».

Рисунок 1.3 – Элемент НЕ

Связь между входом х этой схемы и выходом z можно записать соотношением Z = , где х читается как «не х» или инверсия.

Если на входе схемы 0, то на выходе 1. Когда на входе 1 на выходе 0.

Таблица 1.3 Таблица истинности элемента «НЕ»

Вход	Выход
a	НЕ a
0	1
1	0

Э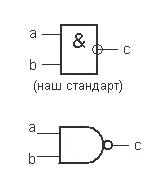 лемент «И-НЕ» (NAND, штрих Шеффера).

Рисунок 1.4 – Элемент И-НЕ

Элемент И-НЕ работает точно так же как «И», только выходной сигнал полностью противоположен. Там где у элемента «И» на выходе должен быть «0», у элемента «И-НЕ» - единица. И наоборот. Это легко понять по эквивалентной схеме элемента:

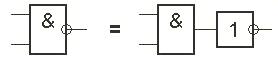
Рисунок 1.5 - Эквивалентная схема элемента И-НЕ

Таблица 1.4 – Таблица истинности элемента «И-НЕ»

Входы		Выход
a	b	с
0	0	1
0	1	1
1	0	1
1	1	0

Э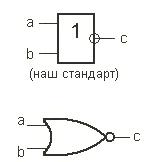 лемент «ИЛИ-НЕ» (NOR, стрелка Пирса).

Рисунок 1.6 – Элемент ИЛИ-НЕ

Мнемоническое правило для ИЛИ-НЕ с любым количеством входов звучит так: На выходе будет:

• «1» тогда и только тогда, когда на всех входах действуют «0»;

• «0» тогда и только тогда, когда хотя бы на одном входе действует «1».

Таблица 1.5 – Таблица истинности элемента «ИЛИ-НЕ»

Входы			Выход
a	b	с
0	0	1
0	1	0
1	0	0
1	1	0