8. Решение систем линейных алгебраических уравнений методом Зейделя.

Процесс (4.22) можно видоизменить, если использовать приближения к решениям, найденные в ходе текущей итерации, при проведении этой же итерации:

	=
	=
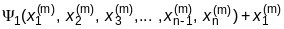
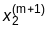
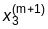
	=		(4.24)
. . . . .	.	. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
	=

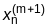
Этот процесс называется методом Зейделя. Он приводит, как правило, к ускоре­нию сходимости по сравнению с процессом (4.22). Еще одним важным преиму­щес­твом метода Зейделя является меньший расход памяти ЭВМ, т.к. при его использо­ва­нии необходим один массив для хранения вектора-столбца приближений, а в методе простых итераций - два: по массиву на предыдущее и текущее приближения.

Для сходимости итерационных методов, т.е. для выполнения условия (4.23) при некотором конечном m, необходимо, чтобы значения диагональных элементов матри­цы СЛАУ были преобладающими по абсолютной величине по сравнению с другими элементами. Обеспечить это требование можно путем перестановки строк и (или) стол­б­­цов матрицы системы.

9. Вычисление определителей методом Гаусса.

При выполнении прямого хода метода Гаусса при решении СЛАУ вычисление по формулам (4.15), (4.16) производится для j=1, ..., n+1, т.е. преобразованию подлежат как коэффициенты при неизвестных x₁,..., x_n, так и свободные члены системы.

Аналогичный алгоритм, но для j=1,...,n, может быть применен для вычисления оп­ре­делителя любой квадратной матрицы порядка n. Подставляя (4.15) в (4.16), полу­чим:

,

(4.17)

где k = 1, ... , n-1 - номер шага преобразования матрицы; i = k+1,...,n ; j = 1,2,...,n.

Так как i изменяется от k+1, то это означает, что первая строка матрицы не изменяется. Преобразование исходной матрицы по формуле (4.17) приводит к треугольной матрице, у которой элементы, расположенные ниже главной диагонали, равны нулю:

			. . .
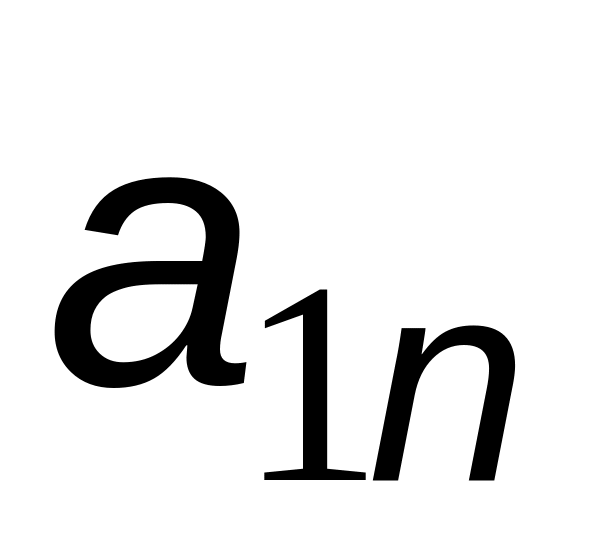
0			. . .
0	0		. . .
. . .	. . .	. . .	. . .	. . .	. . .
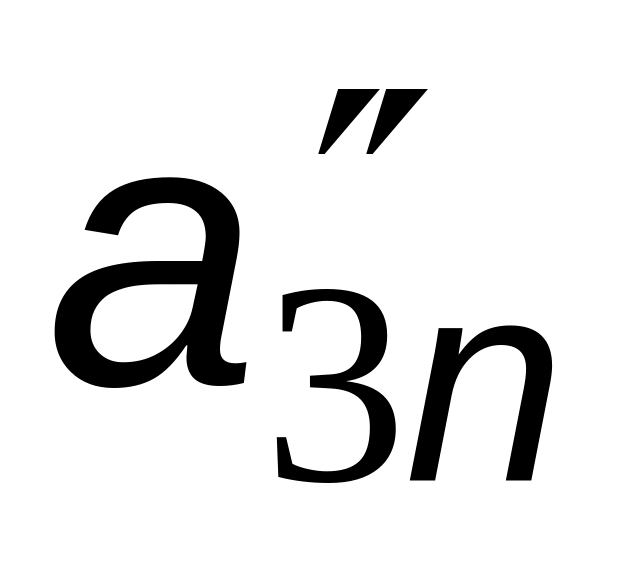
0	0	0	. . .
0	0	0	. . .	0

Преобразование (4.17) является линейным и поэтому не приводит к изменению опре­делителя матрицы; но так как преобразованная матрица - треугольная, то ее оп­редели­тель равен произведению элементов главной диагонали. В отличие от решения СЛАУ здесь не требуется выполнение обратного хода.

Для получения максимальной точности результата надо стремиться, как и при решении СЛАУ, к тому, чтобы на каждом k-ом шаге преобразования на месте элемента а_kk находился максимальный по модулю элемент из тех, что стоят в k-ом столбце ниже k-ой строки. Это достигается процедурой выбора главного элемента, поэтому при вы­числении определителя надо учитывать, что перестановка любых двух строк матрицы приводит к изменению знака определителя на противоположный.