Вычисление определенных интегралов Требуется вычислить интеграл вида

,	(6.1)

где  f(x) - подынтегральная функция, непрерывная на [a,b];

a,b - нижний и верхний пределы интегрирования. Геометрически вычисление определенного интеграла интерпретируется как вычисление площади, ограниченной осью OX и графиком f(x) на промежутке [a,b] изменения х (рис.6.1). К численному вычислению интеграла (чис­ленному интегрированию) обращаются в случаях, когда невозможно аналитически записать первообразную интеграла:   через элементарные функции или если такая запись имеет очень сложный вид.

Геометрическая интерпретация определенного интеграла

Суть большинства методов численного интегрирования состоит в замене подынтегральной функции  f(x) аппроксимирующей функцией  , для которой можно легко записать первоообразную в элементарных функциях, т.е.

,

где S - приближенное значение интеграла (6.1);

R - погрешность численного вычисления интеграла J.

16. Методы прямоугольников вычисления определенных интегралов.

Данные методы относятся к простейшим из класса методов Ньютона-Котеса. В них подынтегральная функция  f(x) на каждом интервале разбиения заменяется полиномом нулевой степени, т.е. константой. Такая замена является неоднозначной, т.к. константу можно выбрать равной значению f(x) в любой точке данного интервала разбиения.

В любом случае значение частичного интеграла определяется как произведение длины интервала разбиения на выбранную константу, т.е. как площадь прямоугольника. В зависимости от способа выбора аппроксимирующей константы различают методы левых, средних или правых прямоугольников (рис.6.4).

Левые

Средние

Правые

Рис.6.4. Геометрическая интерпретация методов прямоугольников

Введем следующие обозначения: точку a на оси OX обозначим через x₀, точку b - через x_n, а точки разбиения промежутка [a,b] - через x₁, x₂,..., x_n-1. Предполагается, что длина интервала разбиения постоянна на всем [a,b]. Обозначим ее через h:

; x_i= x_i-1 + h, i =1,2,...,N.

Тогда в методе левых прямоугольников площадь каждого i-го прямоугольника

Si = h f(xi), i = 0,1,2,...,n-1,

(6.2)

а для всего промежутка [a,b]:

Аналогично, в методе правых прямоугольников

Si = h f(xi), i = 1,2,...,n; .

(6.3)

и в методе средних прямоугольников

Si = h 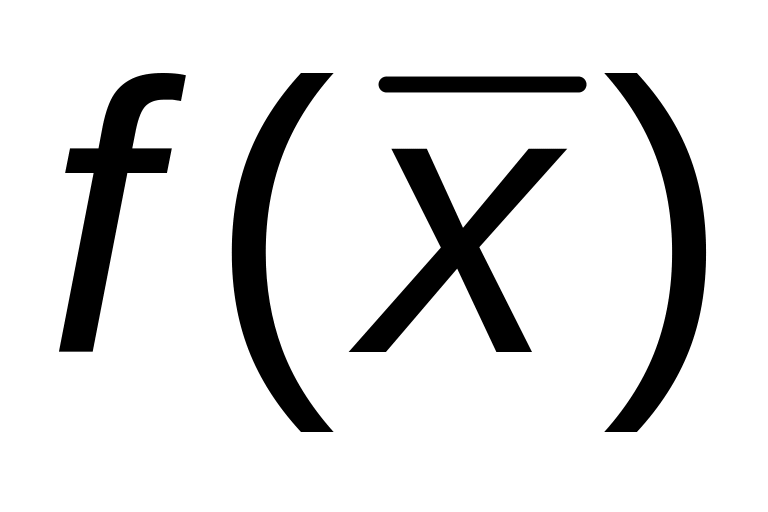), i = 0,1,2,...,n-1; ,

(6.4)

где  , i = 0,1,2,...,n-1.

Приведенные формулы для S являются вычислительными формулами методов прямоугольников.

На рис.6.5. приведена блок-схема вычисления определенного интеграла методом средних прямоугольников.

Рис.6.5. Алгоритм метода средних прямоугольников

Алгоритмы для методов левых и правых прямоугольников отличаются от изображенного на рис.6.5 лишь одним блоком (он выделен жирной линией). Для метода левых прямоугольников здесь должно стоять X=A, для метода правых прямоугольников должно быть X=A+h.

Метод средних прямоугольников имеет меньшую погрешность по сравнению с методом левых или правых прямоугольников и за счет коэффициента в знаменателе (24 > 2), и за счет интеграла от производной, т.к. для большинства функций выполняется неравенство .

Следовательно, использование метода средних прямоугольников является предпочтительным, но использовать его удается не всегда. Если значения  f(x) определяются из эксперимента в дискретном наборе узлов, то метод средних прямоугольников напрямую при­менить нельзя из-за отсутствия значений f(x) в срединных точках. В этой ситуации приходится применять либо какие-нибудь средства интерполяции, что приводит к дополнительным расходам машинного времени и памяти, либо другие методы численного интегрирования.