Решение трансцендентных уравнений

1. Решение трансцендентных уравнений методом дихотомий.

Во многих инженерных и научных задачах возникает необходимость решения уравнений вида:

F(x, a1, a2, ..., ak) = 0

(3.1)

где F - заданная непрерывная функция;

x – неизвестная величина, подлежащая определению;

a₁, a₂, ..., a_k – известные параметры функции F.

Решить уравнение (3.1) - это значит найти такое значение (или такие значения) неизвестной x, при которых уравнение (3.1) превращается в тождество. Эти значения x называются корнями уравнения (3.1).

Только для простейших уравнений удается найти решение в аналитическом виде, т.е. записать формулу

x = f(a₁, a₂, ..., a_k) ,

выражающую искомую величину x явным образом через параметры a₁, a₂, ..., a_k, например, для уравнения вида

ax² + bx + c = 0

его корни выражаются формулой:

.

В большинстве же случаев аналитическую запись корней уравнения найти очень сло­ж­но или в принципе невозможно (такие уравнения называются трансцендентными), и по­это­му приходится решать уравнение численным способом.

Метод дихотомии

Пусть на этапе отделения корней получены две точки A и B (A<B), между которыми находится корень уравнения (3.1), т.е. такие точки, в которых знаки значений функ­ции F(x) противоположны (см. рис.3.2): sign F(A)  sign F(B).

Метод дихотомии, называемый еще методом половинного деления, заключается в следующем:

1) определяется середина отрезка [A,B]:

;

(3.2)

2) вычисляется значение функции в этой точке - F(P) и его знак sign F(P);

3) корень уравнения (3.1) находится в той половине отрезка [A,B], на концах которой функция F(x) имеет разные знаки. Если это будет половинка [A,P], то перенесем точку B в точку P; если же половинка [P,B], то перенесем точку A в точку P. Благодаря этой операции длина отрезка [A,B], на котором находится корень уравнения, уменьшилась вдвое, т.е. можно сказать, что значение корня определено с точностью до длины полученного отрезка.

Каждое новое повторение действий 1,2,3 будет давать все более точные значения корня уравнения. Повторение этого процесса следует прекращать, когда длина отрезка [A,B] станет меньше заранее заданного значения , являющегося в данном случае ошиб­кой ограничения, т.е. неравенство

B - A <

(3.3)

является критерием окончания вычислительного процесса.

Если величина задана очень малая, то вблизи корня значения F(x) могут ока­заться сравнимыми с погрешностью ее вычисления, т.е. при подходе к корню вычисли­тельный процесс может попасть в так называемую "полосу шума", и дальнейшее уточне­ние корня окажется невозможным. Поэтому кроме точности надо задавать в алгоритме ширину "полосы шума" ₁ и прекращать процесс при попадании в него, т.е. неравенство F(P) | < ₁ является дополнительным критерием окончания вычислительного процесса.

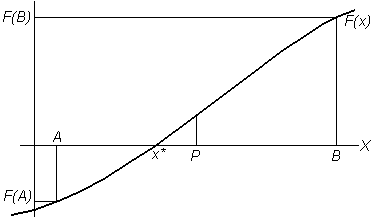
Рис.3.2. Геометрическая интерпретация метода дихотомии