
- •Аксиомы статики. Момент силы относительно центра или оси.
- •Законы Амантона-Кулона о трении.
- •Центр параллельных сил. Методы, применяемые при определении положения центра тяжести однородного тела.
- •Траектория, скорость, ускорение точки. Вычисление векторов скорости и ускорения точки при координатном и естественном способе задания ее движения.
- •Вычисление скорости и ускорение любой точки тела, вращающегося вокруг неподвижной оси.
- •Способы вычисления ускорения точки плоской фигуры в данный момент времени.
- •Сложное движение точки. Теоремы сложения скоростей и ускорений при сложном движении точки.
- •Основные законы механики. Две основные задачи динамики материальной точки.
- •Дифференциальные уравнения вращательного, поступательного и плоскопараллельного движения.
- •Классификация связей. Возможные скорости и возможные перемещения механической системы и материальной точки.
- •Общее уравнение динамики.
- •Уравнение Лагранжа 2-ого рода.
Вычисление скорости и ускорение любой точки тела, вращающегося вокруг неподвижной оси.
С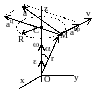 корости
и ускорения точек вращающегося тела.
корости
и ускорения точек вращающегося тела.
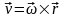 – скорость любой точки твердого тела,
вращающегося вокруг неподвижной оси,
равна векторному произведению вектора
угловой скорости тела на радиус–вектор
этой точки. Модуль векторного произведения:
v=rsin()=
(CM),
(СМ) – расстояние от точки М до оси
вращения. Направлен вектор скорости по
касательной к окружности, по которой
перемещается точка М, в сторону вращения.
– скорость любой точки твердого тела,
вращающегося вокруг неподвижной оси,
равна векторному произведению вектора
угловой скорости тела на радиус–вектор
этой точки. Модуль векторного произведения:
v=rsin()=
(CM),
(СМ) – расстояние от точки М до оси
вращения. Направлен вектор скорости по
касательной к окружности, по которой
перемещается точка М, в сторону вращения.
Формулы
Эйлера:
 ,
,
x,y,z
– проекции вектора угловой скорости.
Проекция вращательной (окружной)
скорости: vx=yz
– zy;
vy=zx
– xz;
vz=xy
– yx.
Если ось вращения совпадает с осью z,
то vx=
– y;
vy=x.
Ускорение:
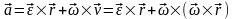 .
Вращательное ускорение
.
Вращательное ускорение
 ,
модуль вращат. уск. авр=rsin,
направлено по касательной к траектории
точки, т.е. параллельно скорости.
Центростремительное (осестремительное)
ускорение
,
модуль вращат. уск. авр=rsin,
направлено по касательной к траектории
точки, т.е. параллельно скорости.
Центростремительное (осестремительное)
ускорение
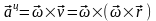 ,
ац=2R,
направлено по радиусу к оси (центру)
вращения. Модуль полного уск.:
,
ац=2R,
направлено по радиусу к оси (центру)
вращения. Модуль полного уск.:
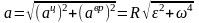 .
Угол, между векторами полного и
центростремит-ного ускорений:
.
Угол, между векторами полного и
центростремит-ного ускорений:
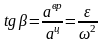 .
.
Плоскопараллельное движение твердого тела. Законы движения.
Плоским (плоскопараллельным) назыв. такое движение, при котором все его точки перемещаются параллельно некоторой неподвижной плоскости. Уравнения плоского движения: xA= f1(t), yA= f2(t), = f3(t), точка А назыв. полюсом. Плоское движение тв.тела слагается из поступательного движения, при котором все точки тела движутся так же, как полюс (А),и из вращательного движения вокруг этого полюса.
Способы вычисления скорости точки плоской фигуры в данный момент времени.
Скорости
точек тела при плоском движении:
 ;
;
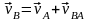 ,
vBA=
BA,
т.е. скорость какой-либо точки В плоской
фигуры равна геометрической сумме
скорости полюса А и скорости точки В
при вращении плоской фигуры вокруг
полюса А.
,
vBA=
BA,
т.е. скорость какой-либо точки В плоской
фигуры равна геометрической сумме
скорости полюса А и скорости точки В
при вращении плоской фигуры вокруг
полюса А.
Теорема: при плоском движении проекции скоростей двух точек тела на ось, проходящую через эти точки, равны между собой: vAcos = vBcos.
М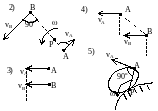 гновенный
центр скоростей
– точка плоской фигуры, скорость которой
в данный момент равна нулю – Р. Если
тело движется непоступательно, т.е. 0,
то мгн.цент.ск. всегда существует. П
гновенный
центр скоростей
– точка плоской фигуры, скорость которой
в данный момент равна нулю – Р. Если
тело движется непоступательно, т.е. 0,
то мгн.цент.ск. всегда существует. П ри
поступательном движении м.ц.с. находится
в .
ри
поступательном движении м.ц.с. находится
в .
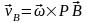 – скорость любой точки плоской фигуры
имеет модуль, равный произведению
угловой скорости фигуры на длину отрезка,
соединяющего точку с м.ц.с., и направлена
этому отрезку в сторону вращения фигуры.
– скорость любой точки плоской фигуры
имеет модуль, равный произведению
угловой скорости фигуры на длину отрезка,
соединяющего точку с м.ц.с., и направлена
этому отрезку в сторону вращения фигуры.
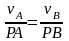 ,
скорости точек тела пропорциональны
их расстояниям до м.ц.с.
,
скорости точек тела пропорциональны
их расстояниям до м.ц.с.
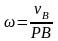 ,
угловая скорость тела равна отношению
скорости какой-нибудь точки к ее
расстоянию до м.ц.с. Определение
положения м.ц.с.:
,
угловая скорость тела равна отношению
скорости какой-нибудь точки к ее
расстоянию до м.ц.с. Определение
положения м.ц.с.:
1) м.ц.с. – точка пересечения перпендикуляров, восстановленных к скоростям точек (напр. в точке В и точке К);
2) если скорости точек А и В параллельны между собой и перпендикулярны АВ, то для определения м.ц.с. должны быть известны модули и направления скоростей (см. vA и vB);
3) если они при этом равны между собой, то м.ц.с. находится в , а угловая скорость =vA/=0;
4) если известно, что скорости двух точек А и В равны, параллельны и не перпендикулярны АВ, то м.ц.с. в , и угловая скорость =vA/=0, если это имеет место только к некоторый момент времени, то имеем мгновенное поступательное движение;
5) если плоская фигура катится без скольжения по неподвижной поверхности, то м.ц.с. плоской фигуры будет в точке соприкасания.
