Аксиомы статики. Момент силы относительно центра или оси.

Аксиомы (законы) статики:

1) аксиома инерции: Под действием взаимно уравновешивающихся сил материальная точка (тело) находится в состоянии покоя или движется прямолинейно и равномерно.

2) аксиома равновесия двух сил: Две силы, приложенные к абсолютно твердому телу, будут уравновешены тогда и только тогда, когда они равны по модулю, действуют по одной прямой и направлены в противоположные стороны.

3) аксиома присоединения и исключения уравновешивающихся сил: Действие системы сил на абс. твердое тело не изменится, если к ней прибавить или отнять уравновешенную систему сил. Следствие: Действие силы на абс.тв. тело не изменится, если перенести точку приложения силы вдоль ее линии действия. Т.е. сила, приложенная к абс.тв. телу– скользящий вектор.

4 ) аксиома параллелограмма сил: Равнодействующая двух пересекающихся сил приложена в точке их пересечения и изображается диагональю параллелограмма, построенного на этих силах. ;

.

5) аксиома равенства действия и противодействия (3-й закон Ньютона): Всякому действию соответствует равное и противоположно направленное противодействие.

6) принцип отвердевания: Равновесие сил, приложенных к нетвердому телу, не нарушается при его затвердевании.

М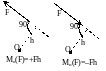 омент силы относительно точки – вектор, численно равный произведению модуля силы на плечо и направленный перпендикулярно плоскости, содержащей силу и точку, в такую сторону, чтобы смотря ему навстречу, видеть силу стремящейся повернуться против хода час.стрелки. Плечо "h"– кратчайшее расстояние от точки до линии действия силы. – момент силы равен векторному произведению вектора 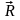на вектор . Модуль векторного произведения: RFsin= Fh. Для плоской сист. сил обычно находят не вектор момента, а только его модуль: Fh, >0 – против час.стр.; <0 – по час.стр.

Свойства момента силы:

1) момент силы не изменяется при переносе точки приложения силы вдоль ее линии действия;

2) момент силы относит. точки =0 только тогда, когда сила =0 или когда линия действия силы проходит через точку (т.е. плечо =0). Если x,y,z – координаты точки приложения силы, F_x, F_y, F_z – проекции силы на оси координат и точка 0 – начало координат, то

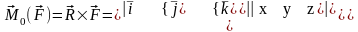=(yF_z – zF_y) +(zF_x – xF_z) +(xF_y – yF_x) , откуда проекции момента силы на оси коорд.: М_0x( )=yF_z – zF_y; М_0y( )=zF_x – xF_z; М_0z( )=xF_y – yF_x.

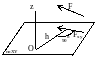
Момент силы относительно оси – скалярная величина, равная моменту проекции этой силы на плоскость, перпендикулярную оси, взятому относительно точки пересечения оси с плоскостью. Момент >0, если смотря навстречу оси, мы видим поворот, который стремится совершить сила направленный против час.стр.

,

На рис. М>0. Момент силы относительно оси равен 0: 1) если сила параллельна оси (F_xy=0), 2) если линия действия силы пересекает ось (h=0); т.е. если ось и сила лежат в одной плоскости. Аналитические выражения моментов силы относительно осей координат: М_x( )=yF_z – zF_y; М_y( )=zF_x – xF_z; М_z( )=xF_y – yF_x.

Главный вектор и главный момент системы сил.

Главный вектор – векторная сумма всех сил, приложенных к телу.

Главный момент относительно центра – векторная сумма моментов всех сил, приложенных к телу относительно того же центра.

Пара сил и ее момент.

Система двух параллельных сил, равных по модулю и направленных в разные стороны, назыв. парой сил. Кратчайшее расстояние между линиями действия этих сил назыв. плечом пары "h". Действия пары сил характеризуется ее моментом. Момент пары сил M = Fh – произведение модуля одной из сил пары на ее плечо.

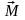
Момент пары сил – вектор, направленный перпендикулярно плоскости сил, так, что, если смотреть ему навстречу, то видим вращение пары против хода час.стр. M>0, если против час.стр., M<0 – по час.стр (на рис М>0).

Содержание метода Пуансо о приведении системы сил к одному центру.

Приведение пространственной системы сил к данному центру решается с помощью теоремы о параллельном переносе силы. Любая система сил, действующих на абс.тв.тело, при приведении к произвольно взятому центру О заменяется одной силой R, равной главному вектору системы и приложенной в центре приведения О, и одной парой с моментом М_О, равным главному моменту системы относительно центра О (главный вектор – векторная сумма всех сил, приложенных к телу; главный момент относительно центра –векторная сумма моментов всех сил, приложенных к телу относительно того же центра).

Необходимое и достаточное условие равновесия системы сил.

Условия равновесия пл. сист. сил: векторное: . аналитич:

, или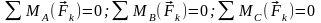

где А,В,С – точки, не лежащие на одной прямой, или , ось "х" не перпендикулярна отрезку АВ.

Теорема об эквивалентности систем сил.

Две системы сил приложенных к свободному твердому телу, эквиваленты тогда и только тогда, когда, когда их главные векторы и главные моменты, относительно одного и того же произвольного центра, равны между собой.

Методы расчета усилий в стержнях фермы.

К ним относятся способ вырезания узлов, способ сечений (метод Риттера).

Способ вырезания узлов заключается в мысленном вырезании узла фермы с заменой действия на него стержней соответствующими усилиями. Эти усилия связаны между собой и приложенной к стержню внешней нагрузкой (или опорными реакциями) посредством статических уравнений равновесия. Для любого узла можно составить два таких уравнения - равенства нулю суммы проекций всех сил, например, на вертикальную и горизонтальную оси. Очевидно, если в узле сходятся два стержня, то из этих уравнений могут быть найдены усилия в обоих из них. Если узел соединяет три стержня, но усилие в одном из ни хуже найдено из рассмотрения равновесия другого узла или использованием способа сечений, то из этих двух уравнений могут быть найдены усилия в двух оставшихся стержнях.

Способ сечений состоит в мысленном рассечении фермы на две части и рассмотрении равновесия одной из них. При этом действие отбрасываемой части на рассматриваемую должно быть заменено усилиями в стержнях ферм. Если провести сечение таким образом, чтобы оно проходило через три стержня, то можно составить уравнения равновесия для рассматриваемой

части фермы таким образом, чтобы найти усилия во всех трех стержнях.